
例1:已知波函数 y=2×10-3c0s(400t-20mx) m 求:A、人九u。 解:由 y=Ac0s2πyt- x + u y=2x0m4o0-0] m A=2×10-3m
例1:已知波函数 2 10 cos(400 20 ) m 3 y = t − x − 求:A、、、u。 解:由 2 10 m −3 A = m 20 2 10 cos 400 3 = − − x y t + = − u x y A cos 2 t
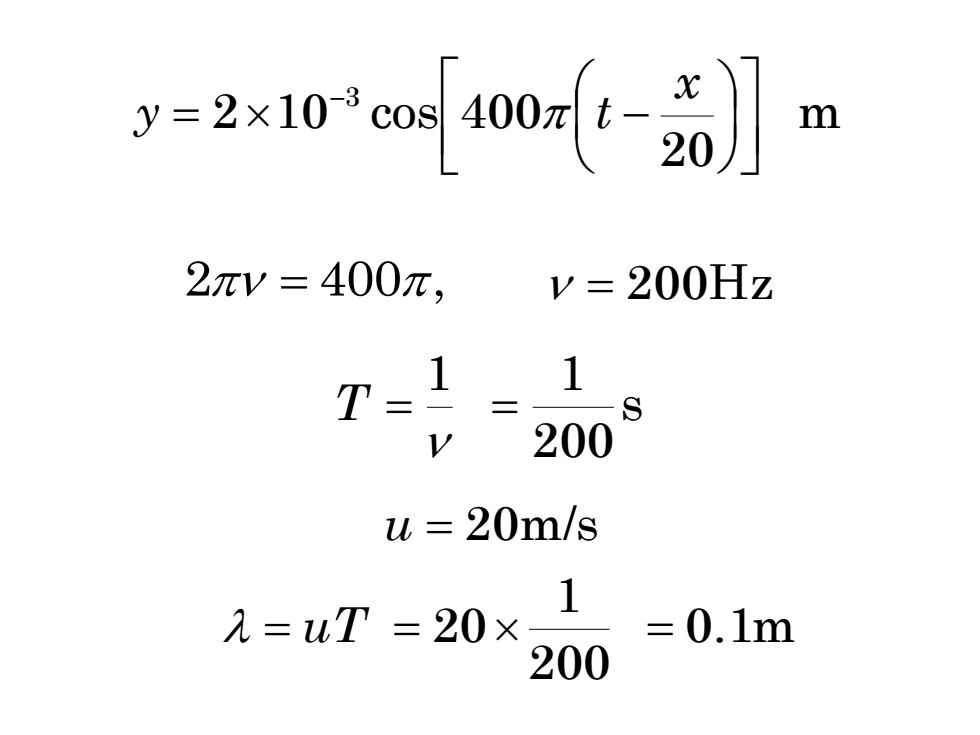
y=2x10oas40s4-20)]m 2πv=400π, 200Hz u 2 m/s 入=uT=20×。 =0.1m 200
2 = 400, = 200Hz 1 T = s 200 1 = m 20 2 10 cos 400 3 = − − x y t 200 1 = 20 u = 20m/s = uT = 0.1m

例2:振源振动方程为y=6×10-2sin800t 波速u=200m/s,求:①波函数; ②波长、频率;③ x=5m处质点振动与 波源的相位差。 解: ①波源 y=6×10-2c0s(800t-π/2) 波函数 x +0 y=6×10os80-260x12
例2:振源振动方程为 y 6 10 sin800t −2 = 波速 ,求:①波函数; ②波长、频率;③ x = 5m 处质点振动与 波源的相位差。 解: ①波源 波函数 + = − u x y A cos t u = 200m/s 6 10 cos(800 / 2) 2 = − − y t − = − − /2 200 6 10 cos 800 2 x y t

②.波长、频率 y=Acoi-x +O y=6x10aa800ft-20a2 0=800元 T= 2π 2元 800元 400 v=1/T=400Hz λ=uT=200/400=0.5m
= 800 2 T = 800 2 = s 400 1 = = 1/T= 400Hz = 200/ 400 = 0.5m ②.波长、频率 + = − u x y A cos t = uT − = − − /2 200 6 10 cos 800 2 x y t

③ x=5m质点振动与波源的相位差。 波源 y=6×10-2c0s(800t-π/2) 5m处 y-6x10eas680m?20)a2 波源的相位 01=800t-π/2 x=5m处相位 p2=800π(t-5/200)-π/2 5 相位差 02-91=800π× =20元 200 P点落后反映在相位上为20π,即振源完成10个 全振动后,P点开始振动
③. x = 5m 处相位 相位差 200 5 2 −1 = 800 P 点落后反映在相位上为 20 , 即振源完成 10 个 全振动后,P 点开始振动。 x = 5m 质点振动与波源的相位差。 波源的相位 1 = 800t − /2 2 = 800 (t − 5/200) − /2 = 20 6 10 cos(800 / 2) 2 = − − y t − = − − /2 200 6 10 cos 800 2 x y t 波源 5m处

例3:如图所示,平面简谐波向右移动速度山=0.08 m/s,求:①.振源的振动方程;②.波函数;③.P 点的振动方程;④。a、b两点振动方向。 解:①.振源 0.04m y=Acos(at+p) 元=2×0.2=0.4m 0.2m T=元/u 0=2t/T=24/=2r×0.08×/0.4=2m/5
例3:如图所示,平面简谐波向右移动速度 u =0.08 m/s,求:①.振源的振动方程;②.波函数;③. P 点的振动方程;④. a、b 两点振动方向。 解:①.振源 o y x u a b P = 20.2= 0.4m 0.2m T = /u = 2 /T = 2u/ y = Acos(t +) = 2 /5 0.04m = 2 0.08 / 0.4
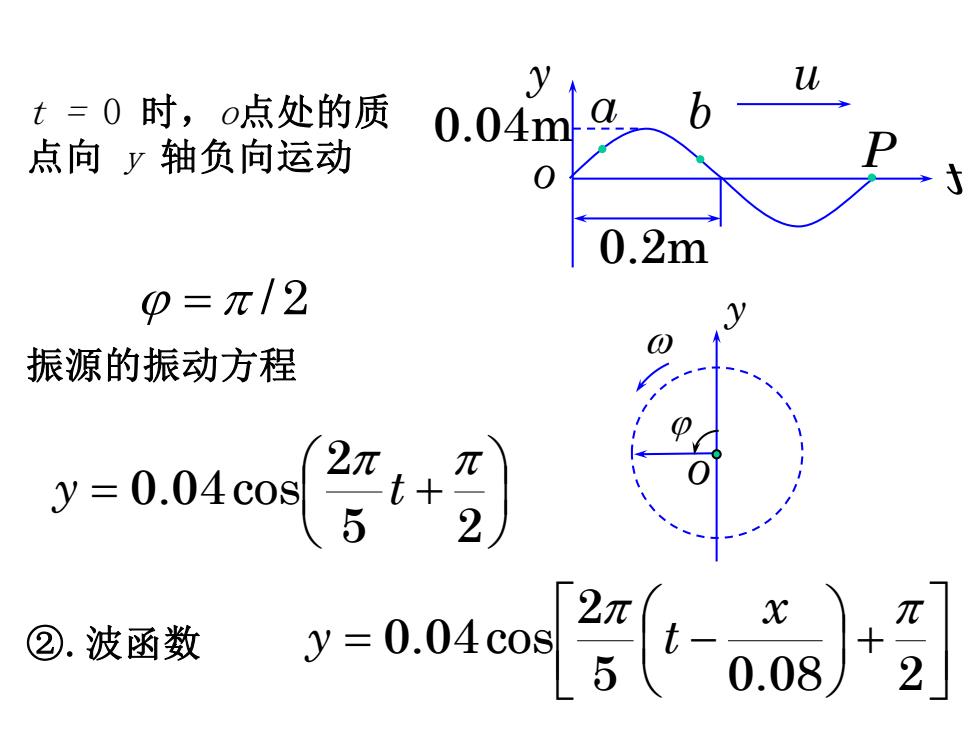
t=0时,o点处的质 0.04m 点向y轴负向运动 0.2m p=π/2 振源的振动方程 y=0.04c0s 5 ②.波函数 y=0.04c0s 0.0R) 2
o y t u a b P 0.2m 0.04m = /2 t = 0 时,o点处的质 点向 y 轴负向运动 ②.波函数 振源的振动方程 = + 5 2 2 0.04cos y t + = − 5 0.08 2 2 0.04cos x y t o y
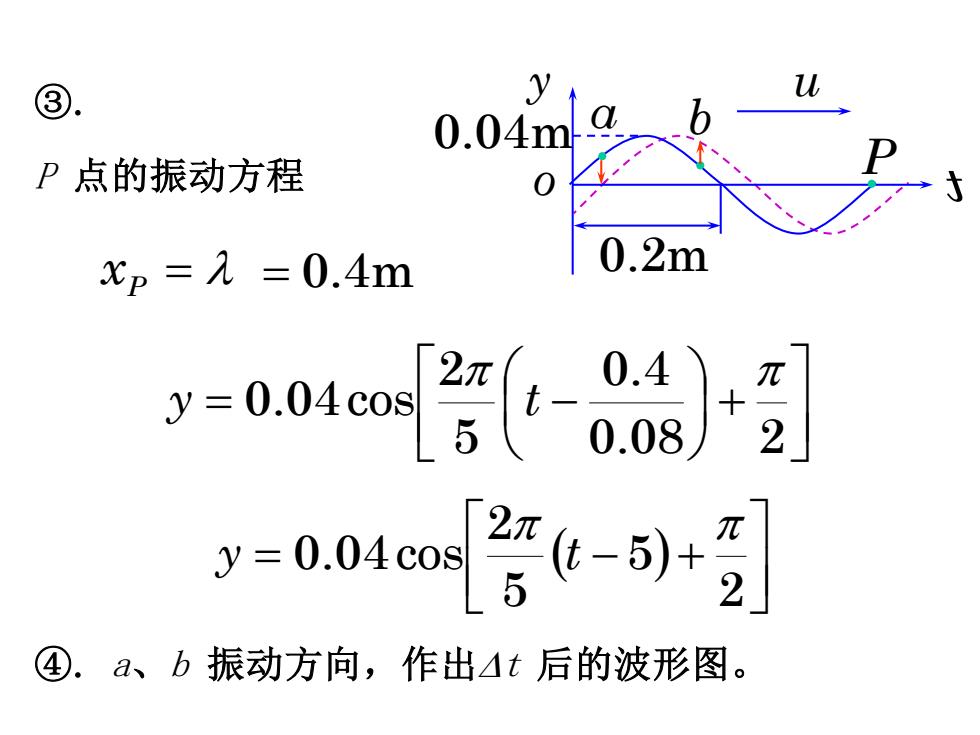
③ 0.04m P点的振动方程 xp=人=0.4m 0.2m y=0.04co 008)2 2n -004a[e-5)- ④.a、b振动方向,作出△t后的波形图
③. P 点的振动方程 xP = = 0.4m + = − 0.08 2 0.4 5 2 0.04cos y t ( ) = − + 2 5 5 2 0.04cos y t ④. a、b 振动方向,作出t 后的波形图。 o y t u a b P 0.2m 0.04m

第二十章波动

教学基本要求 掌握描述简谐波的各物理量及各量间的 关系; 二理解机械波产生的条件.掌握由已知质 点的简谐运动方程得出平面简谐波的波函数的方 法.理解波函数的物理意义.了解波的能量传播特 征及能流、能流密度概念
教学基本要求 一 掌握描述简谐波的各物理量及各量间的 关系; 二 理解机械波产生的条件. 掌握由已知质 点的简谐运动方程得出平面简谐波的波函数的方 法. 理解波函数的物理意义. 了解波的能量传播特 征及能流、能流密度概念