
第9拿恒定做圪 磁约束核聚变研究装置
第9章 恒定磁场 磁约束核聚变研究装置
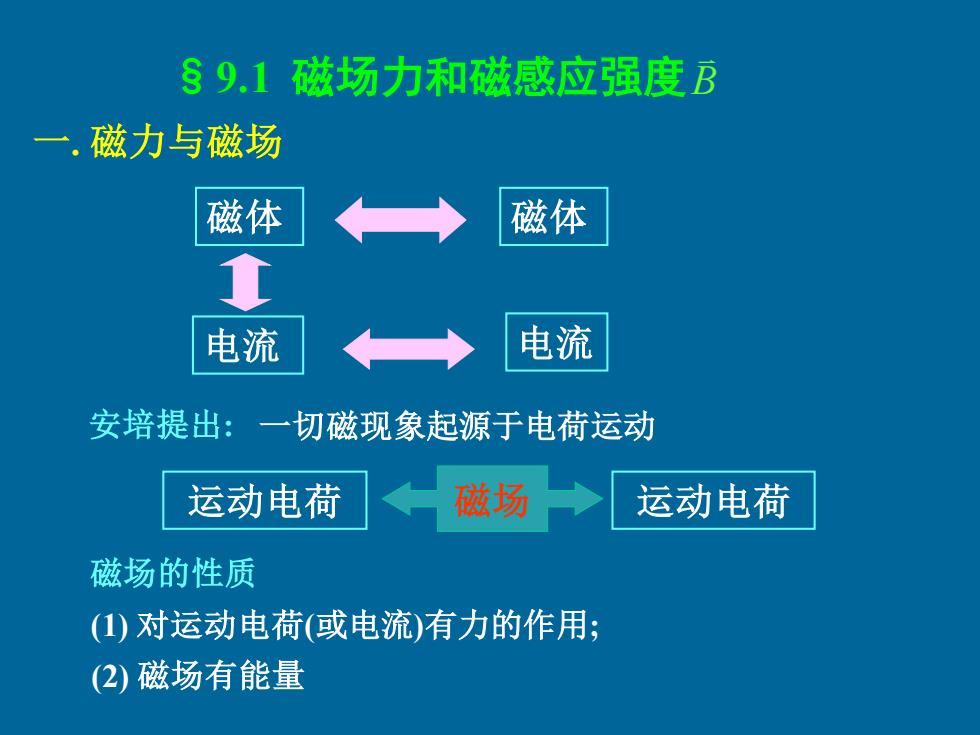
89.1磁场力和磁感应强度B 一.磁力与磁场 磁体 磁体 电流 电流 安培提出:一 切磁现象起源于电荷运动 运动电荷 磁场 运动电荷 磁场的性质 (1)对运动电荷(或电流)有力的作用; (2)磁场有能量
§9.1 磁场力和磁感应强度 一. 磁力与磁场 磁体 磁体 电流 电流 安培提出: 一切磁现象起源于电荷运动 运动电荷 磁场 运动电荷 磁场的性质 (1) 对运动电荷(或电流)有力的作用; (2) 磁场有能量 B
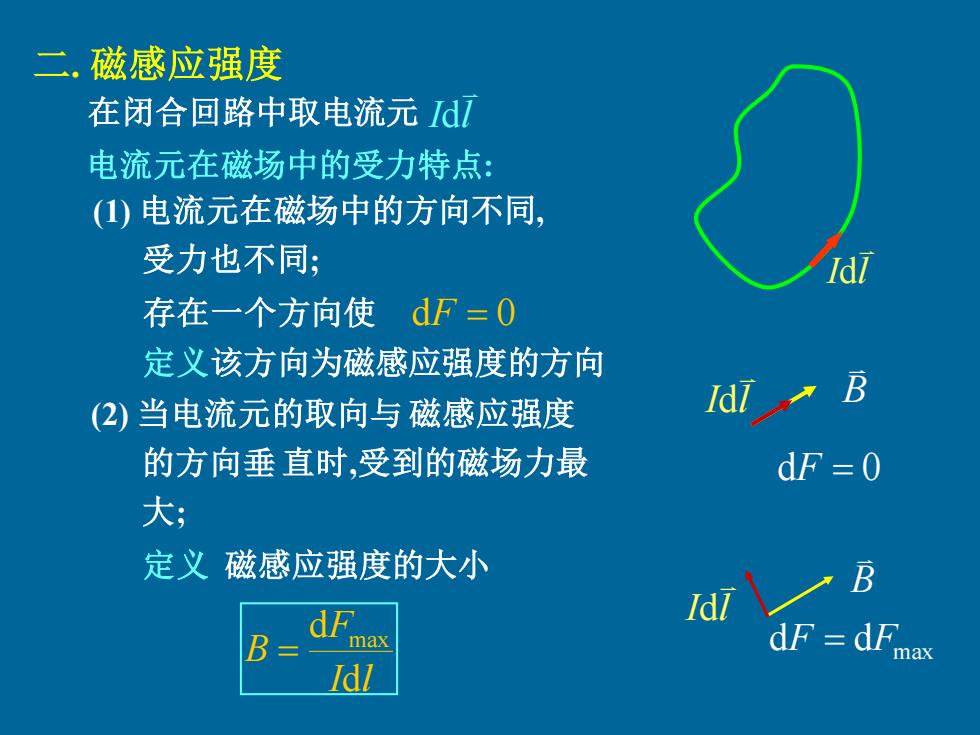
二,磁感应强度 在闭合回路中取电流元Idl 电流元在磁场中的受力特点: (1)电流元在磁场中的方向不同, 受力也不同; 1d7 存在一个方向使dF=0 定义该方向为磁感应强度的方向 (2)当电流元的取向与磁感应强度 Idl B 的方向垂直时,受到的磁场力最 dF =0 大 定义磁感应强度的大小 dF Idl B max dF dF max
二. 磁感应强度 在闭合回路中取电流元 I l d I l d 电流元在磁场中的受力特点: (1) 电流元在磁场中的方向不同, 受力也不同; 存在一个方向使 dF = 0 I l d dF = 0 定义 I l F B d d max = B (2) 当电流元的取向与 磁感应强度 的方向垂 直时,受到的磁场力最 大; 磁感应强度的大小 定义该方向为磁感应强度的方向 B I l d dF = dFmax
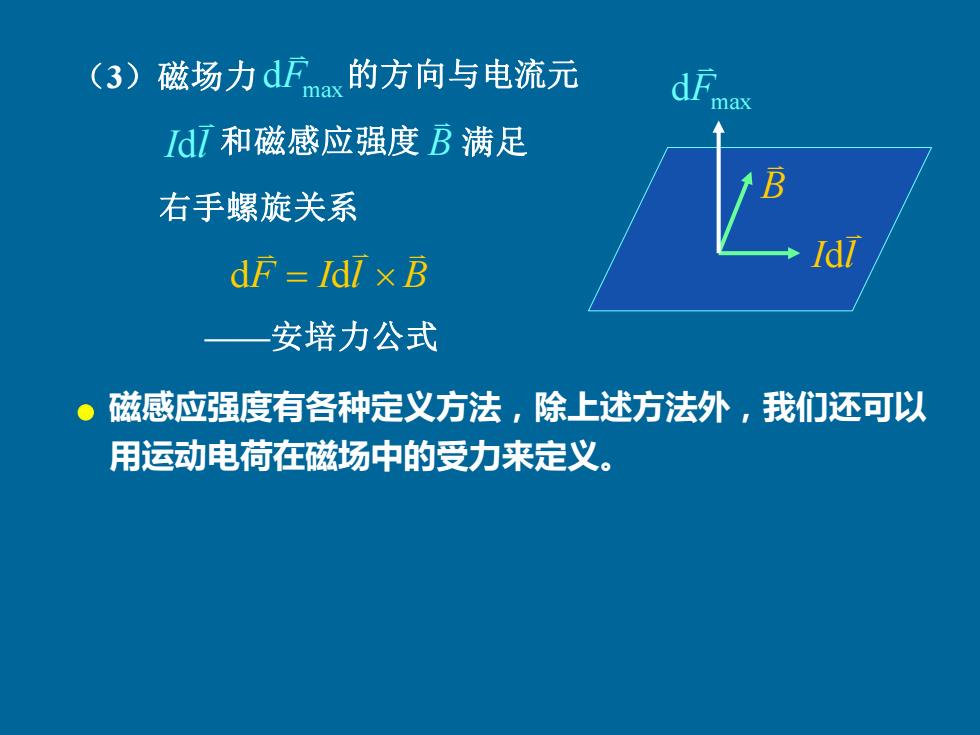
(3) 磁场力dFm的方向与电流元 dF ax IdI和磁感应强度B满足 右手螺旋关系 dF Idl x B 安培力公式 ● 磁感应强度有各种定义方法,除上述方法外,我们还可以 用运动电荷在磁场中的受力来定义
满足 dFmax I l d B dFmax F I l B d = d (3)磁场力 的方向与电流元 和磁感应强度 B ——安培力公式 I l d 右手螺旋关系 磁感应强度有各种定义方法,除上述方法外,我们还可以 用运动电荷在磁场中的受力来定义

§9.2毕奥一萨伐尔定律 一.毕奥一萨伐尔定律 静电场:取dg →d万 E=dE 磁场:取Id7 -9dB 毕一萨定律: dB=4aM×万 一单位矢量 4元 4=4元×107N/A2 真空中的磁导率 大小: :dB=4 dlsin B 4π 方向:右螺旋法则 d
§9.2 毕奥-萨伐尔定律 一.毕奥-萨伐尔定律 静电场: 取 dq E d E = E d 磁 场: 取 I l d B d B = B d 2 0 0 d 4 d r I l r B = 毕-萨定律: 0 r 单位矢量 真空中的磁导率 7 2 0 4 10 N A − = 大小: 2 0 d sin 4 d r I l B = 方向:右螺旋法则 ? P I l d r B

例如: B B=0 r IdI r 二.毕一萨定律的应用 1.载流直导线的磁场 求距离载流直导线为α处 一点P的磁感应强度 解 dB=toIdlsin 4π 8-a-经m0
例如: I l d P I l d I l r d B r B r B r B = 0 二.毕-萨定律的应用 1. 载流直导线的磁场 I a I l d r B 解 2 0 d sin 4 d r I l B = 求距离载流直导线为a处 一点P 的磁感应强度 B 2 0 d sin 4 d r I l B B = = P
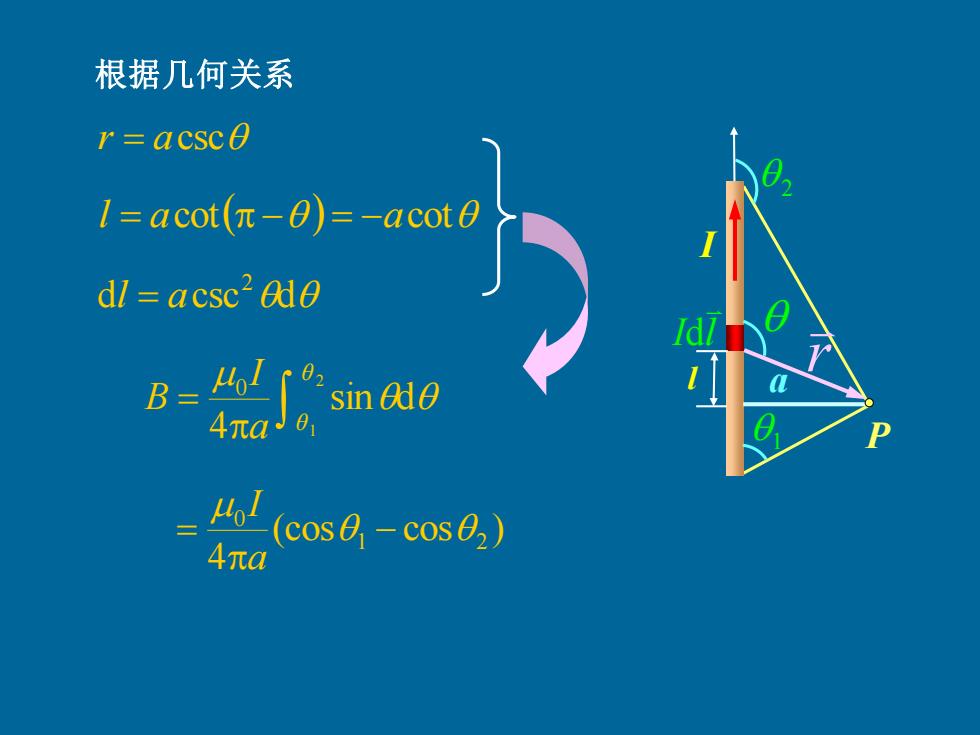
根据几何关系 r acsco 1=acot(π-O)=-acot0 dl acsc2 0d0 B= sin ado 4πaJ8 D 编csA-c风)》
1 2 r = acsc d csc d 2 l = a l = acot( − ) = −acot 根据几何关系 (cos cos ) 4 1 2 0 − = a I = 2 1 sin d 4 0 θ a θ I B I a I l d r P l
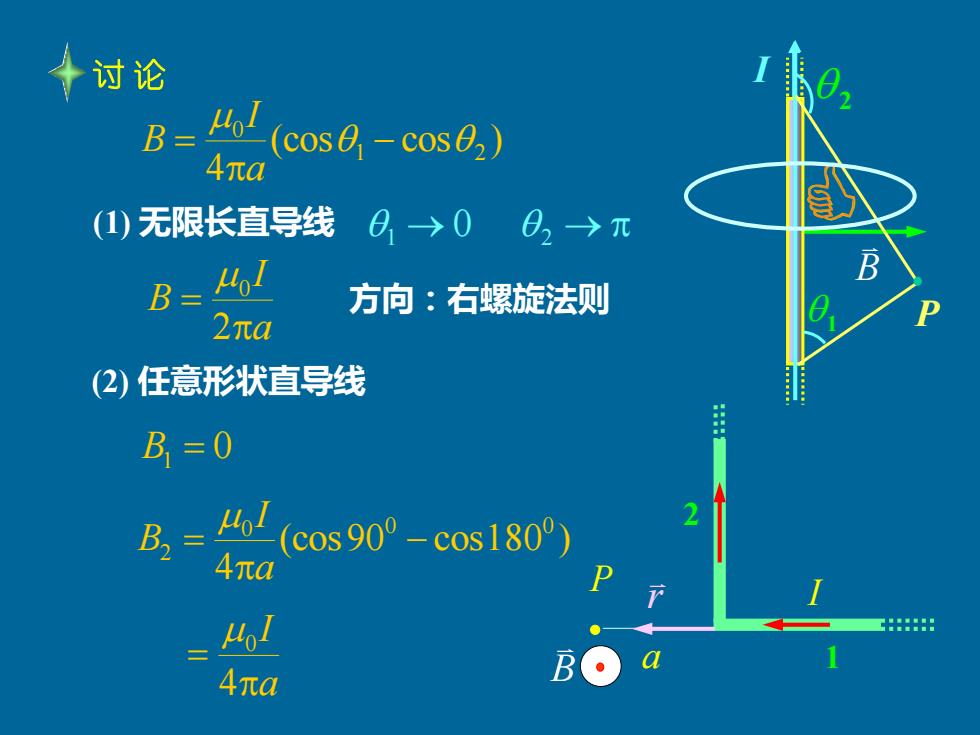
十讨论 B= (cos0-cos0,) 4πa (1)无限长直导线0,→0 02→元 B=46I 方向:右螺旋法则 2πa (2)任意形状直导线 B=0 B,=6/(cos90°-c0s180) 2 4元a 46 C::8 4πa B
(1) 无限长直导线 (cos cos ) 4 1 2 0 − = a I B 1 → 0 2 → a I B = 2 0 方向:右螺旋法则 B (2) 任意形状直导线 P a I 1 2 B1 = 0 (cos90 cos180 ) 4 0 0 0 2 − = a I B a I = 4 0 B r 讨 论 I 1 2 P
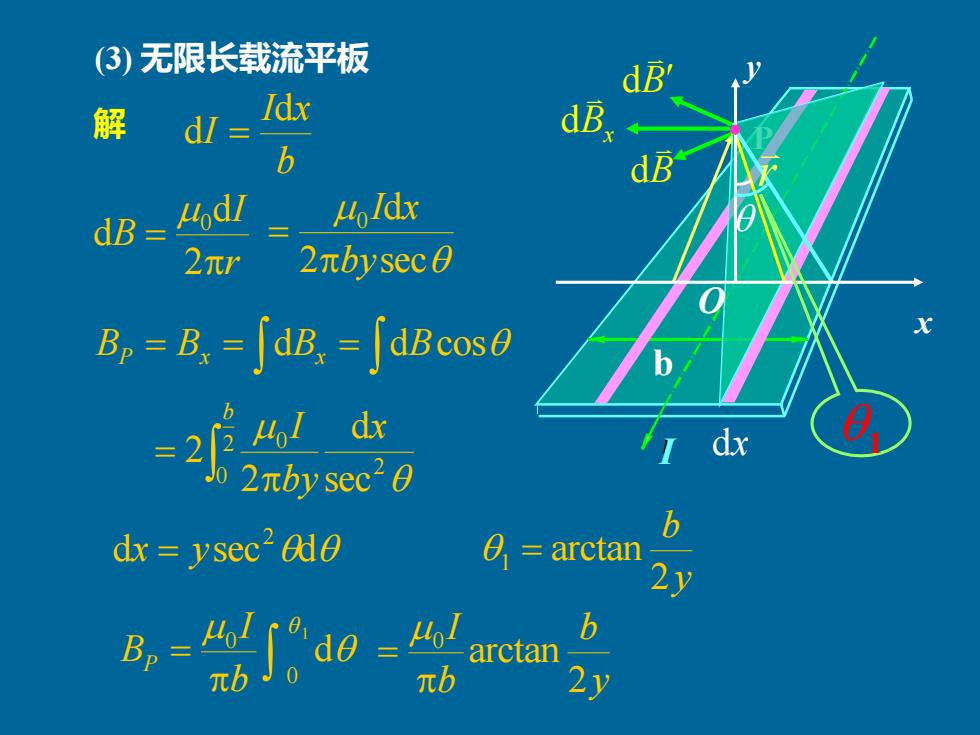
(③)无限长载流平板 解 Idx d/ dB. b dB dB d 461d 2π 2πbysec0 B,=B,=∫dB=∫dBcos0 。 dx dx ysec2ade 0 arctan 21 0=4 b arctan
I b (3) 无限长载流平板 P B d Bx 解 d b I x I d d = r I B = 2 d d 0 BP = Bx = Bx d = dBcos = 1 0 0 d θ P b I B y b b I 2 arctan 0 = d sec d 2 x = y r 2 sec d 0 by I x = = 2 0 2 0 sec d 2 2 b x by I x y O dx y b 2 1 = arctan B d 1
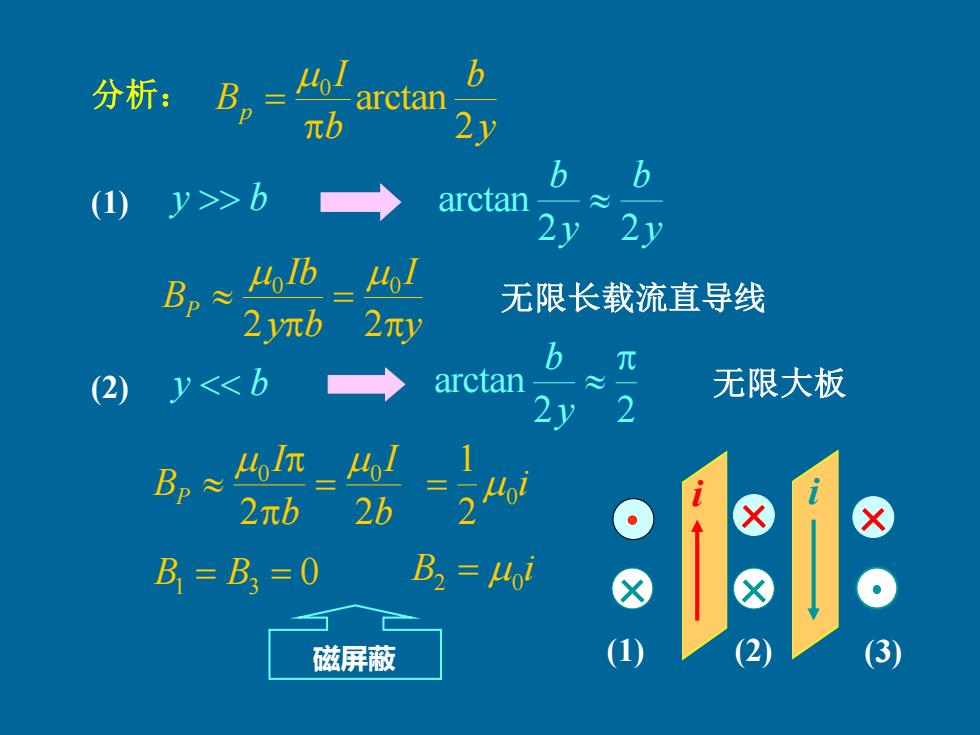
b 分析: B =o! arctan πb 2y (1) y>>b arctan 无限长载流直导线 2yπb b (2 <<6 arctan 无限大板 2y B2≈ 4π 41 2πb B=B3=0 B2=4o1 磁屏蔽 3
(1) (2) (3) 分析: y b b I Bp 2 arctan 0 = (1) y b y I y b Ib BP = 2 2 0 0 y b y b 2 2 arctan 无限长载流直导线 (2) y b 2 2 arctan y b b I b I BP 2 2 0 0 = i 0 2 1 = 无限大板 0 B1 = B3 = B i 2 = 0 磁屏蔽 i i