广东工业大学：《大学物理》课程教学课件（PPT讲稿）第八章 静电场 §8.5 电势 电势差 §8.6 等势面 电势与电场强度的微分关系 §8.7 静电场中的导体 §8.8 电场能量 §8.9 静电场中的电介质

88.5电势 电势差 一，电势 单位正电荷自a-→b过 电势差 程中电场力作的功。 单位正电荷自 该点→“势能 电势定义 零点”过程中 电场力作的功。 → ,=4gw=Ed ·点电荷的电势 4=E.d7 E= dl dr r 4π80 d7

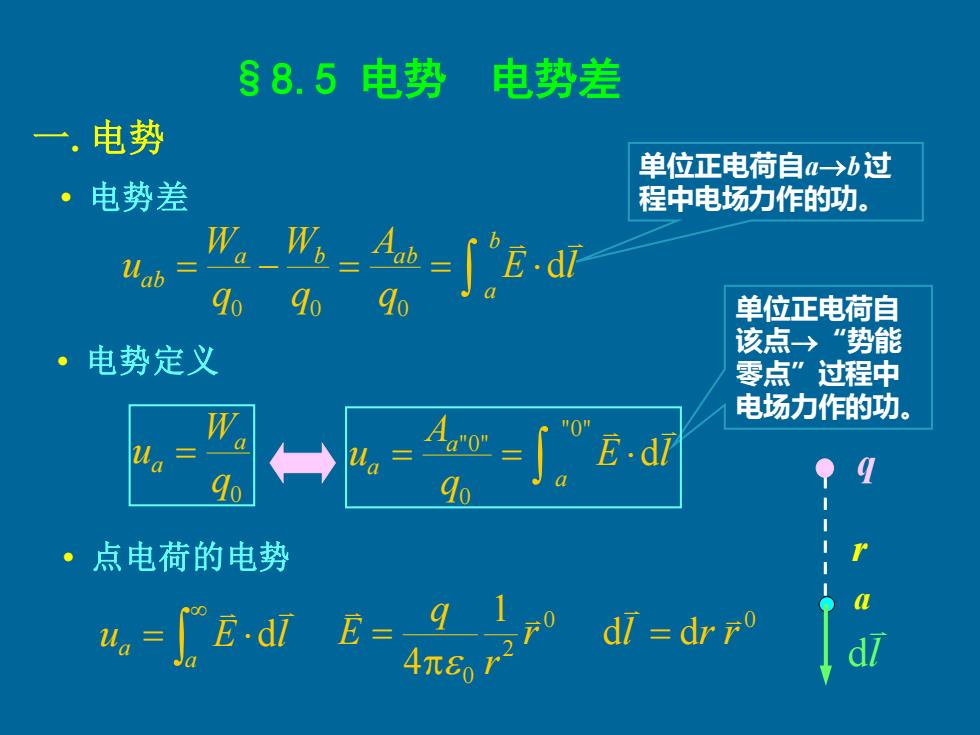
§8.5 电势 电势差 • 电势差 一. 电势 单位正电荷自a→b 过 程中电场力作的功。  = − = =  b a a b a b a b E l q A q W q W u   d 0 0 0 q0 W u a a =  = =  "0" 0 "0" d a a a E l q A u   • 电势定义 单位正电荷自 该点→ “势能 零点”过程中 电场力作的功。 a r l  d q • 点电荷的电势   =  a a u E l   d 0 2 0 1 4 r r q E    = 0 dl dr r   =

ua 4π80 4π801 二.电势叠加原理 ·点电荷系的电势 929 =+d-4n h4π802 2 4πE 4π8o3 对n个点电荷 台4π i=l

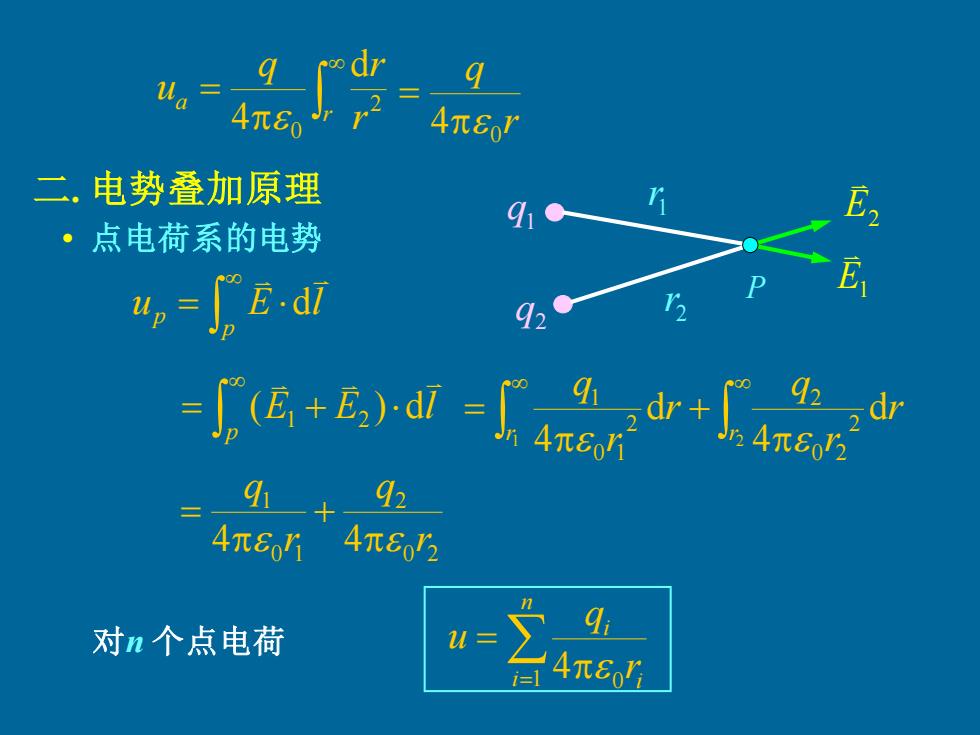
   = r a r q r u 2 0 d 4  r q 4 0  = 二. 电势叠加原理 • 点电荷系的电势   =  p p u E l   d q1 q2 E1  E2  1 r 2 r P   = +  p E E l    ( ) d 1 2      +  = 1 2 d 4 d 4 2 0 2 2 2 0 1 1 r r r r q r r q   0 2 2 0 1 1 4 4 r q r q   +  = 对n 个点电荷 =  = n i i i r q u 1 0 4 

在点电荷系产生的电场中，某点的电势是各个点电荷单独存 在时，在该点产生的电势的代数和。这称为电势叠加原理。 对连续分布的带电体 04π8 三，电势的计算 (1) 已知电荷分布 = dq 04π81 方法 (2) 已知场强分布 u,=∫Edl

在点电荷系产生的电场中，某点的电势是各个点电荷单独存 在时，在该点产生的电势的代数和。这称为电势叠加原理。 对连续分布的带电体   = Q r q u 4 0 d  三.电势的计算 方法 （1） 已知电荷分布   = Q r q u 4 0 d  （2） 已知场强分布  =  "0" d p p u E l  

例均匀带电圆环半径为R,电荷线密度为几。 求圆环轴线上一点的电势 解建立如图坐标系，选取电荷元dq dq dg Adl R dq Adl du 4πEòr 4π60VR2+x2 P 2元R 2πR入 up Jo 4πeVR2+x2 4πE√R2+x

r q u 4 0 d d  = 2 2 4 0 d R x l  + =      + = R p R x l u 2 0 2 2 4 0 d   2 2 4 0 2 R x R  +  =   均匀带电圆环半径为R，电荷线密度为。 解 建立如图坐标系，选取电荷元dq 例 求 圆环轴线上一点的电势 dq = dl R P O x dq r

例半径为R,带电量为g的均匀带电球体 求带电球体的电势分布 解根据高斯定律可得： r<R E= 4π6R r≥R E2= q 4π6 对球外一点P 4π801 对球内一点P Edr-drr3R)

半径为R ，带电量为q 的均匀带电球体 解 根据高斯定律可得： 求 带电球体的电势分布 例 + + + + + + R r P r  R 3 0 1 4 R qr E  = r  R 2 0 2 4 r q E  = 对球外一点P 对球内一点P1 u E r p   d 1 =    内    = + R R r E dr E dr 1 2 (3 ) 8 2 2 3 0 R r R q −  =  u E r p   d 2 =    外    = r r q r 2 4 0 d  r q 4 0  = P1

s8.6 等势面 电势与电场强度的微分关系 一，等势面 电场中电势相等的点连成的面称为等势面。 等势面的性质： (1)E⊥等势面

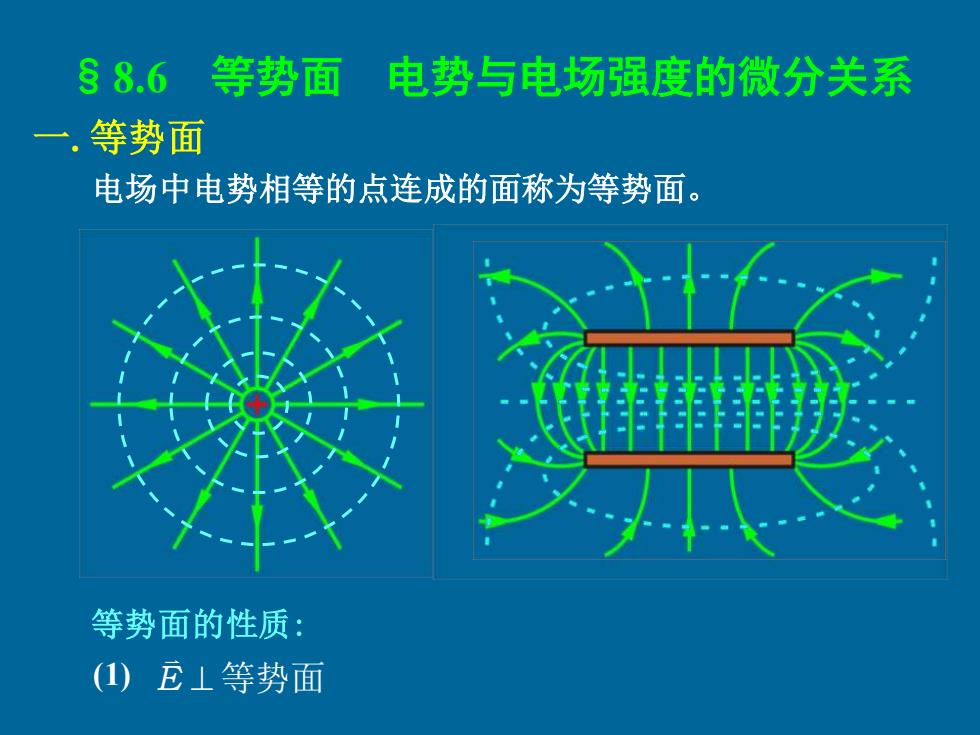
§8.6 等势面 电势与电场强度的微分关系 一. 等势面 电场中电势相等的点连成的面称为等势面。 等势面的性质: (1) E ⊥ 等势面 

证明：设等势面上P点的电场强度与等势面夹角为8， 把qo在等势面上移动d,电场力作功为 dA=goE.dI go E cosedi =qo(4p-4o) 4p=4g .goE cosdl=0 COS=0 2 (2)规定相邻两等势面间的电势差都相同 等势面密→E大 等势面疏◆ E小 (③)电场强度的方向总是指向电势降落的方向

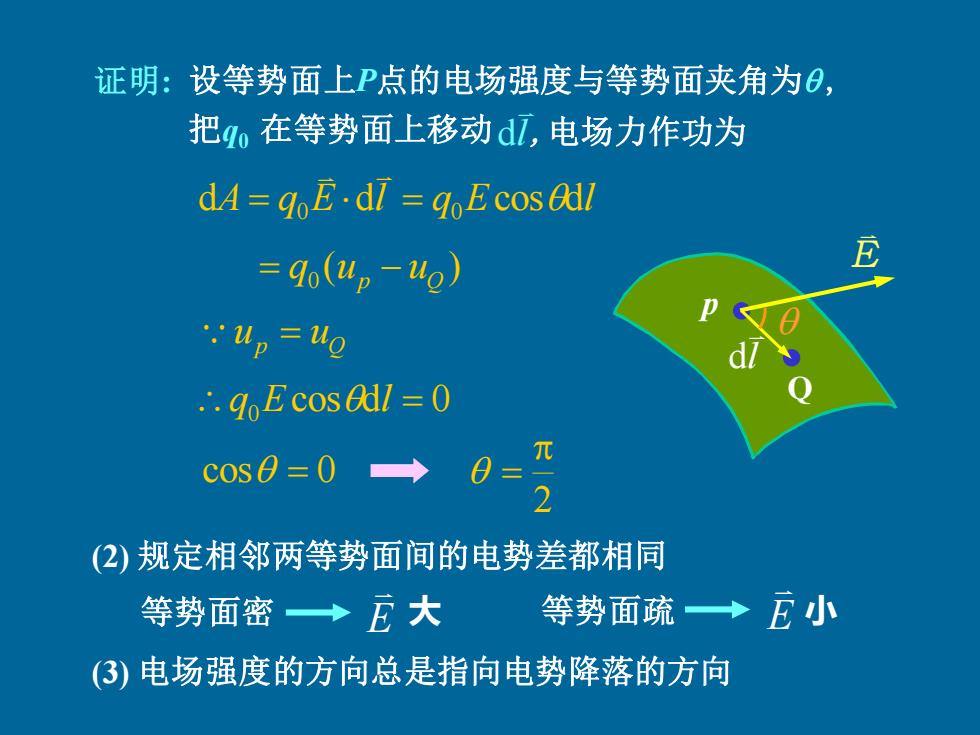
证明: dA q E dl q Ecos dl = 0  = 0    ( ) 0 p Q = q u − u p Q u = u q0Ecosdl = 0 cos = 0 2   = (2) 规定相邻两等势面间的电势差都相同 等势面密 E  大 等势面疏 E  小 p Q l  d E   (3) 电场强度的方向总是指向电势降落的方向 设等势面上P点的电场强度与等势面夹角为 , 把q0 在等势面上移动 l ,电场力作功为  d

二.电势与电场强度的微分关系 取两个相邻的等势面，等势面法线方向为，设E的方向与 相同，把点电荷从P移到Q,电场力作功为： d4=qE·dl=qE cos @dl gEdn dA=glu-(u+du)]=-qdu E cos edl Edn =-du E=- du dn 任意一场点处电场强度的大小等于沿过该点等势面法线方 向上电势的变化率，负号表示电场强度的方向指向电势减 小的方向

u u+du 二. 电势与电场强度的微分关系 取两个相邻的等势面，等势面法线方向为 = qEdn dA = qE dl = qEcosdl   dA = q[u − (u + du)] = −qdu n u E d d = − Ecosdl = Edn = −du E   n  d 任意一场点P处电场强度的大小等于沿过该点等势面法线方 向上电势的变化率，负号表示电场强度的方向指向电势减 小的方向。 n 把点电荷从P移到Q，电场力作功为：  n  ，设 E  的方向与 n  相同， P Q l  d

另一种理解 Ecos0 dl Edn=-du du E,dl=-du dl 电场强度在1方向的投影等于电势沿该方向变化率的负值 dl≥dn du du dl dn 电势沿等势面法线方向的变化率最大 在直角坐标系中 E、 E 8x E,= 8y 0z

在直角坐标系中 Ecosθ dl = Edn = −du 另一种理解 Eldl = −du l u El d d = − dl  dn n u l u d d d d  x u Ex   = − y u Ey   = − z u Ez   = − 电势沿等势面法线方向的变化率最大 电场强度在 l 方向的投影等于电势沿该方向变化率的负值

E= k)=-grad(u 某点的电场强度等于该点电势梯度的负值，这就是电势与 电场强度的微分关系。 例已知u=6x-6x2y-7z2 求(2,3,0)点的电场强度。 解 Ou =-(6-12xy)=66 Bx u E=一 =6x2=24 F.=_ =-14z=0 y E=E1+E,7=66i+24)

某点的电场强度等于该点电势梯度的负值，这就是电势与 电场强度的微分关系。 ( k ) grad(u) z u j y u i x u E = −   +   +   = −     例 求（2，3，0）点的电场强度。 已知 2 2 u = 6x − 6x y − 7z 解 = −(6 −12 ) = 66   = − xy x u Ex 6 24 2 = =   = − x y u Ey E E i E j i j x y      = + = 66 + 24 = −14 = 0   = − z z u Ez