
第九章 三休和电个质中感中 导体和介介质2 导体和介质3 导体和介质4
第九章 导体和介介质2 导体和介质3 导体和介质4

§9-1静电场中的导体 一.导体的静电平衡条件 1.静电感应现象 a.静电感应:外电场的作 用导致导体中电荷重新分 布而呈现出带电的现象 b.静电平衡状态:导体内部和表面上都 没有电荷的定向移动状态
一 .导体的静电平衡条件 1.静电感应现象 a.静电感应:外电场的作 用导致导体中电荷重新分 布而呈现出带电的现象 − A − + + + B b.静电平衡状态:导体内部和表面上都 没有电荷的定向移动状态 §9-1静电场中的导体
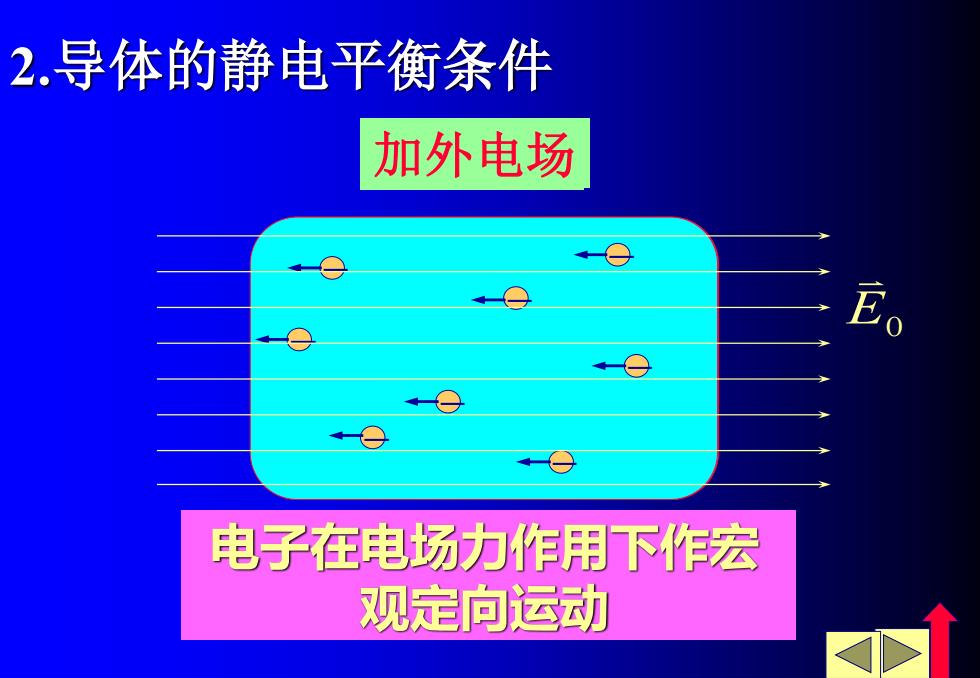
2.导体的静电平衡条件 加外电场 电子在电场力作用下作宏 观定向运动
2.导体的静电平衡条件 − − − − − − − − 无外电场 电子和晶格点阵作随机的 微观热运动 − − − − − − − − 电子在电场力作用下作宏 观定向运动 E0 加外电场
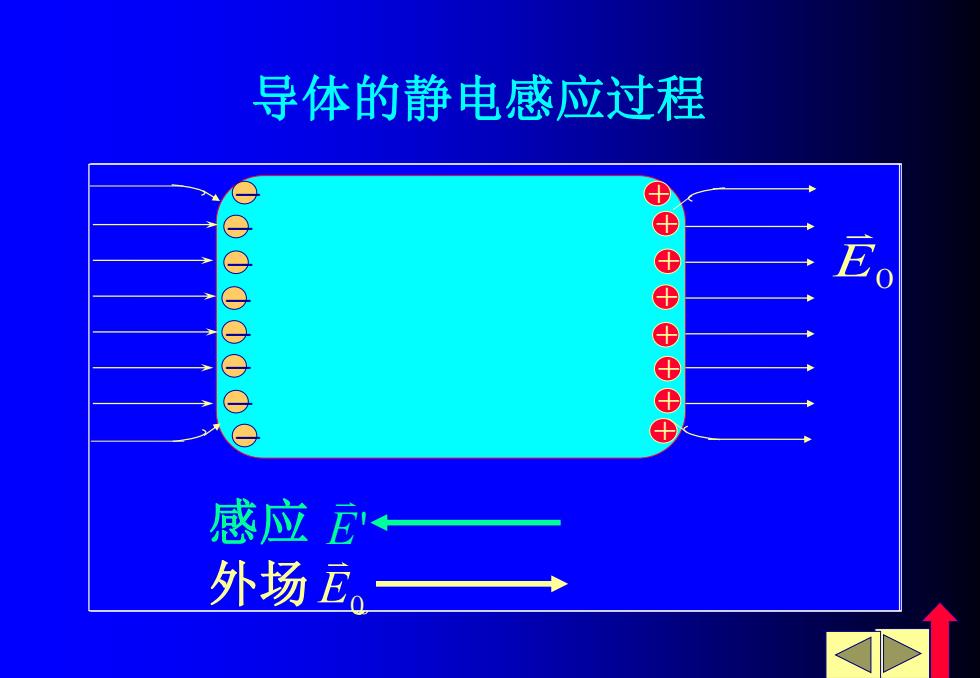
导体的静电感应过程 ⊕ 0004040 +++++++ Eo 感应E◆ 外场龙
− − − − − − − − E0 外场 感应 E' E0 导体的静电感应过程 − − − − − − − − + E0 E' E0 − − − − − − − − + E0 + E' E0 − − − − − − − − + E0 + + 感应 E' E0 − − − − − − − − + E0 + + + E' E0 − − − − − − − − + E0 + + + + E' E0 − − − − − − − − + E0 + + + + + E' E0 − − − − − − − − + E0 + + + + + + E' E0 − − − − − − − − + E0 + + + + + + + E' E0
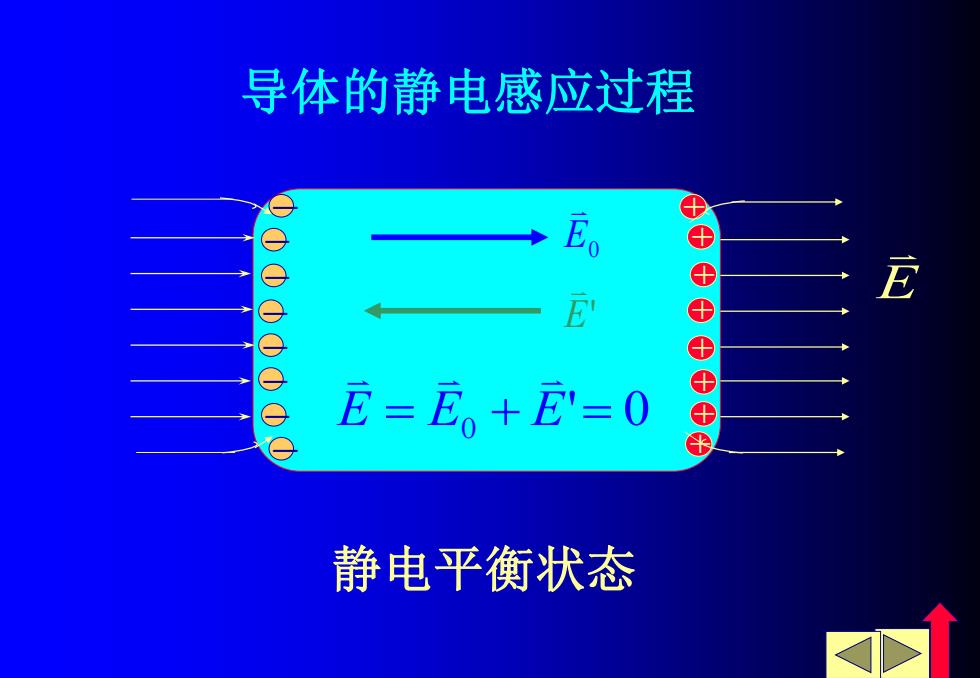
导体的静电感应过程 +++ E=E。+E=0 ++十 静电平衡状态
− − − − − − − − + 导体的静电感应过程 E + + + + + + + 静电平衡状态 E0 E' E = E0 + E' = 0

(1).静电平衡条件: a.导体内部任何一点的场强为零 b.导体表面上任何一点的场强方向垂直 于该点的表面 (2).等价条件: 静电平衡时,导体为等势体
(1).静电平衡条件: a.导体内部任何一点的场强为零 b.导体表面上任何一点的场强方向垂直 于该点的表面 (2).等价条件: 静电平衡时,导体为等势体

证:设a和b为静电平衡导体上任意两点 单位正电荷由a移到b,电场力的功为 ∫Edl=U。-U=AU (.a、b在导体内部: .E=0.△乙J=0 (2).a、b在导体表面 .ELdn.E.d=0即△U=0 静电平衡的导体是等势体
a b b a E dl =U −U a b = U 证:设a和b为静电平衡导体上任意两点 单位正电荷由a移到b,电场力的功为 (1).a、b在导体内部: E = 0 U = 0 (2).a、b在导体表面: E dl ⊥ E dl = 0 即 U = 0 -静电平衡的导体是等势体
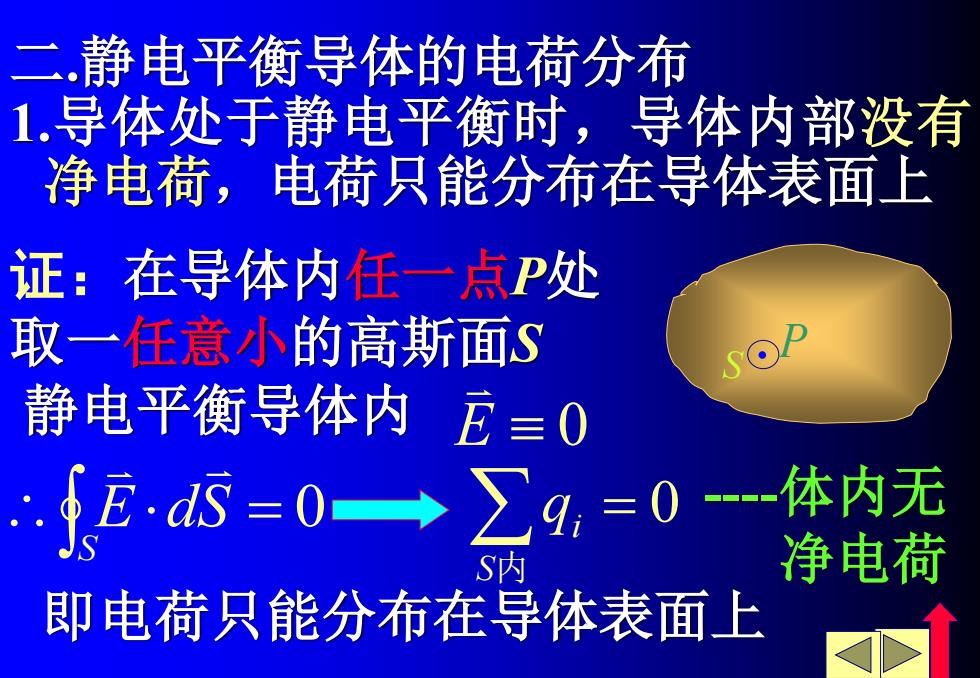
二.静电平衡导体的电荷分布 1.导体处于静电平衡时,导体内部没有 净电荷,电荷只能分布在导体表面上 证:在导体内任一点P处 取一任意小的高斯面S 静电平衡导体内龙≡0 .fEs=0→∑g,=0 -体内无 S内 净电荷 即电荷只能分布在导体表面上
二.静电平衡导体的电荷分布 1.导体处于静电平衡时,导体内部没有 净电荷,电荷只能分布在导体表面上 证:在导体内任一点P处 取一任意小的高斯面S P S = S E dS 0 = 0 S内 i q 静电平衡导体内 E 0 即电荷只能分布在导体表面上 -体内无 净电荷

2.有空腔的导体:设空腔导体带电荷Q 空腔内没有电荷时:导 体内部和空腔内表面上 都没有净电荷存在,电 荷只分布在导体外表面 证:在导体内作一包围空腔的高斯面S 导体内E=0.E·dS=0 即 ∑9,=0S内无净电荷存在 S内
2.有空腔的导体:设空腔导体带电荷Q + + + + + + + + + + + + + + + + 空腔内没有电荷时:导 Q 体内部和空腔内表面上 都没有净电荷存在,电 荷只分布在导体外表面 S 证:在导体内作一包围空腔的高斯面 S = S E dS 0 E 0 导体内 = 0 S内 i 即 q -S内无净电荷存在

问题:会不会出现空腔内表面分布有等 量异号电荷的情况呢? 空腔内有电荷时:空腔内表面感应出 等值异号电量-9,导体外表面的电量为 导体原带电量Q与感应电量q的代数和 由高斯定理和电荷 守恒定律可证
问题:会不会出现空腔内表面分布有等 量异号电荷的情况呢? 空腔内有电荷q时:空腔内表面感应出 等值异号电量-q,导体外表面的电量为 导体原带电量Q与感应电量q的代数和 + + + + + + + + + + + + + + + + Q + q + q − − − − − − − − − q 由高斯定理和电荷 守恒定律可证