
第12卷第3期 智能系统学报 Vol.12 No.3 2017年6月 CAAI Transactions on Intelligent Systems Jun.2017 D0I:10.11992/tis.201704038 网络出版地址:htp:/kns.cmki.net/kcms/detail/23.1538.TP.20170705.1653.002.html 一 种融合DGSOM神经网络的仿生算法研究 许瞳,凌有铸,陈孟元 (安徽工程大学安徽省电气传动与控制重点实验室,安徽芜湖241000) 摘要:基于生理学和脑科学研究成果提出的SOM神经网络仿生优化方法能够通过学习自主绘制出拓扑地图,但需 通过大量的尝试确定其初始网络结构,无法保证系统的实时性。提出一种方向信息和特征信息构建的动态增长自 组织特征网DG$OM,通过引入方向参数减少网络的训练次数.降低了系统复杂度,通过引入特征参数避免了感知混 淆,并将该神经网络模型应用于澳大利亚Milford等提出的RatSLAM模型中。实验表明,提出的DGSOM-RatSLAM模 型通过减少视觉细胞的数量降低系统的复杂度:通过视觉细胞的场景匹配实验和位姿细胞的活性状态实验证明该 模型能够更快地实现闭环检测,提出的DGSOM-RatSLAM模型的准确率、召回率及F,值分别为94.74%、86.88%和 90.64%,高斯噪声干扰下Guss-DGs0M-RatSLAM模型的准确率、召回率及F,值分别为86.70%、80.25%、83.35%。 关键词:RatSLAM模型:DGSOM神经网络:同步定位与地图构建:闭环检测:准确率:召回率 中图分类号:TP242.6:TP183文献标志码:A文章编号:1673-4785(2017)03-0405-08 中文引用格式:许瞳,凌有铸,陈孟元.一种融合DGS0M神经网络的仿生算法研究[J】.智能系统学报,2017,12(3):405-412。 英文引用格式:XU Tong,LING Youzhu,CHEN Mengyuan.Abio-inspired algorithm integrated with DGSOM neural network[J]. CAAI transactions on intelligent systems,2017,12(3):405-412. A bio-inspired algorithm integrated with DGSOM neural network XU Tong,LING Youzhu,CHEN Mengyuan (Anhui Key Laboratory of Electric Drive and Control,Anhui Polytechnic University,Wuhu 241000,China) Abstract:Based on physiology and brain science,self-organizing-map (SOM)neural networks can learn and autonomously draw topological maps,but the initial SOM network structure must be repeatedly tested,so the real- time characteristics of the system cannot be assured.In this paper,we built a dynamic growing self-organizing map (DGSOM)based on direction and feature parameters that reduces network training times by the introduction of the direction parameter and decreases system complexity and avoids perceptual aliasing by the introduction of the feature parameter.By introducing the feature parameter,we can avoid perception confusion.We applied the proposed model to the view cells of the simultaneous localization and mapping system (SLAM)known as RatSLAM, proposed by Milford et al.Our experimental results show that the proposed DGSOM-RatSLAM model can decrease the complexity of the system by reducing the quantity of view cells and realize closed-loop detection earlier by matching the scene with view cells and detecting on the activity of the pose cells.We found the precision rate, recall rate,and F value of the DGSOM-RatSLAM model to reach 94.74%,86.88%,and 90.64%,respectively, and those of the Gauss-DGSOM-RatSLAM model to reach 86.70%,80.25%,and 83.35%,respectively. Keywords:RatSLAM model;DGSOM neural network;simultaneous localization and mapping;closed-loop detection;precision rate;recall rate 在生物神经系统中,存在着一种侧抑制现象, 抑制作用,这种抑制作用会使神经细胞之间出现竞 个神经细胞的兴奋会对周围其他神经细胞产生 争,从而造成神经细胞的兴奋或抑制。1982年芬兰 Helsink大学的T.Kohonen教授)基于这种现象提 收稿日期:2017-04-25.网络出版日期:2017-07-05. 基金项目:安徽高校自然科学研究项目(K2016A794). 出一种自组织特征图(self-organizing feature map, 通信作者:凌有铸.E-mail:yz7985@163.com
第 12 卷第 3 期 智 能 系 统 学 报 Vol.12 №.3 2017 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2017 DOI:10.11992 / tis.201704038 网络出版地址:http: / / kns.cnki.net / kcms/ detail / 23.1538.TP.20170705.1653.002.html 一种融合 DGSOM 神经网络的仿生算法研究 许曈,凌有铸,陈孟元 (安徽工程大学 安徽省电气传动与控制重点实验室,安徽 芜湖 241000) 摘 要:基于生理学和脑科学研究成果提出的 SOM 神经网络仿生优化方法能够通过学习自主绘制出拓扑地图,但需 通过大量的尝试确定其初始网络结构,无法保证系统的实时性。 提出一种方向信息和特征信息构建的动态增长自 组织特征网 DGSOM,通过引入方向参数减少网络的训练次数,降低了系统复杂度,通过引入特征参数避免了感知混 淆,并将该神经网络模型应用于澳大利亚 Milford 等提出的 RatSLAM 模型中。 实验表明,提出的 DGSOM⁃RatSLAM 模 型通过减少视觉细胞的数量降低系统的复杂度;通过视觉细胞的场景匹配实验和位姿细胞的活性状态实验证明该 模型能够更快地实现闭环检测,提出的 DGSOM⁃RatSLAM 模型的准确率、召回率及 F1 值分别为 94.74%、86.88%和 90.64%,高斯噪声干扰下 Gauss⁃DGSOM⁃RatSLAM 模型的准确率、召回率及 F1 值分别为 86.70%、80.25%、83.35%。 关键词:RatSLAM 模型;DGSOM 神经网络;同步定位与地图构建;闭环检测;准确率;召回率 中图分类号:TP242.6;TP183 文献标志码:A 文章编号:1673-4785(2017)03-0405-08 中文引用格式:许曈,凌有铸,陈孟元.一种融合 DGSOM 神经网络的仿生算法研究[J]. 智能系统学报, 2017, 12(3): 405-412. 英文引用格式:XU Tong, LING Youzhu, CHEN Mengyuan. A bio⁃inspired algorithm integrated with DGSOM neural network[J]. CAAI transactions on intelligent systems, 2017, 12(3): 405-412. A bio⁃inspired algorithm integrated with DGSOM neural network XU Tong, LING Youzhu, CHEN Mengyuan (Anhui Key Laboratory of Electric Drive and Control, Anhui Polytechnic University, Wuhu 241000, China) Abstract:Based on physiology and brain science, self⁃organizing⁃map ( SOM) neural networks can learn and autonomously draw topological maps, but the initial SOM network structure must be repeatedly tested, so the real⁃ time characteristics of the system cannot be assured. In this paper, we built a dynamic growing self⁃organizing map (DGSOM) based on direction and feature parameters that reduces network training times by the introduction of the direction parameter and decreases system complexity and avoids perceptual aliasing by the introduction of the feature parameter. By introducing the feature parameter, we can avoid perception confusion. We applied the proposed model to the view cells of the simultaneous localization and mapping system (SLAM) known as RatSLAM, proposed by Milford et al. Our experimental results show that the proposed DGSOM⁃RatSLAM model can decrease the complexity of the system by reducing the quantity of view cells and realize closed⁃loop detection earlier by matching the scene with view cells and detecting on the activity of the pose cells. We found the precision rate, recall rate, and F1 value of the DGSOM⁃RatSLAM model to reach 94.74%, 86.88%, and 90.64%, respectively, and those of the Gauss⁃DGSOM⁃RatSLAM model to reach 86.70%, 80.25%, and 83.35%, respectively. Keywords: RatSLAM model; DGSOM neural network; simultaneous localization and mapping; closed⁃loop detection; precision rate; recall rate 收稿日期:2017-04-25. 网络出版日期:2017-07-05. 基金项目:安徽高校自然科学研究项目(KJ2016A794). 通信作者:凌有铸. E⁃mail:lyz7985@ 163.com 在生物神经系统中,存在着一种侧抑制现象, 一个神经细胞的兴奋会对周围其他神经细胞产生 抑制作用,这种抑制作用会使神经细胞之间出现竞 争,从而造成神经细胞的兴奋或抑制。 1982 年芬兰 Helsink 大学的 T.Kohonen 教授[1] 基于这种现象提 出一种自组织特征图( self⁃organizing feature map

·406· 智能系统学报 第12卷 SOM),并引入赢者通吃(winner take all,.WTA)理 1.1 位姿细胞的活性状态变化 论,该仿生优化方法通过学习能够自主绘制出拓扑 创建的兴奋度权重矩阵ε和由于兴奋性使位 地图,但需通过大量的尝试确定其初始网络结构, 姿感知细胞活动产生的变化APyg如式(1)和式 无法保证系统的实时性能,研究者们基于该模型的 (2)所示: 缺陷进行了改进。1993年Martinetz等2)提出一种 1 (1) 神经气(neural gas,NG)模型,提高了网络自组织学 ky√2pk, 习过程的效率。2004年尹峻松等[)为克服S0M孤 NN Na 立学习与噪声敏感等缺陷,结合一氧化氮(N0)扩 △Pg= 散机理,在SOM网中引入时间增强机制,提出了一 式中:ky和ke分别为位姿感知细胞平面(x',y)和 种新型扩散的自组织模型(diffusing self-.organizing 0'维中对应着兴奋性一维分布的方差常数;a、b、c分 maps,DS0M)。2009年王春东等[4)将S0M理论运 别为x'y'、'的分布系数;N、N,、N分别为(x',y', 用于信息学,利用灰色关联系数(grey relational )空间中的位姿感知细胞三维矩阵元素:抑制常数 coefficient,.GRC)调整权重,检测拒绝服务攻击 ”控制全局抑制水平,使兴奋度被限制在非负范 (denial of service,DOS)。20ll年于乃功等[s]将可 围内。 增长特征映射图(growing self-organizing map, 1.2视觉细胞的场景学习及位姿关联 GSOM)融入双目立体视觉,通过自组织拓扑结构避 ~维视觉细胞通过视觉关联影响位姿细胞活 免了传统SOM网需大量实验才能确定的初始网络 性状态,其连接强度a。如式(3)所示: 结构。本文以GSOM神经网络模型为基础引入了 awy=ai,Pyo,Vi (3) 方向参数和特征参数构成的动态增长自组织特征 视觉细胞关联下的位姿细胞网络活性如式(4) dynamic growing self-organizing feature map, 所示: DGSOM),并应用于澳大利亚Milford等[6]提出的 APyg=δ∑awywVi (4) RatSLAM模型中。 式中δ为视觉校准加强常数。 1 RatSLAM模型 1.3经历图的构建 经验E、编码位姿细胞P、视觉细胞V和经历间 由于传感器和环境的不确定性,移动机器人利 的拓扑关系d如式(5)所示: 用概率解决同步定位与地图构建问题。其中,卡尔 E=P,V,d (5) 曼滤波、极大期望估计和粒子滤波3种概率算法是 拓扑关系d如式(6)所示: 当前移动机器人SLAM的核心技术,其通过专用网 N 格或拓扑地图的方式进行环境描述,这些研究成果 △d:=a[ (d,-d-△P)+ 在仿真和限定条件下能够取得良好效果,但难以兼 顾实际环境,且存在计算量大、搜索时间长、易于陷 三d-4-ar,门 (6)】 入局部最优解等问题。 式中:α为学习常量:N是从经历i到其他经历的转 鼠类是生物医学研究最多的动物之一【10川,人 移个数:N,是从其他经历到经历i的转移个数。实 们对于其导航、环境探索和真实神经机制的模拟理 验表明,学习常量α取0.5可使构建的地图收敛到 解得很好,因此鼠类成为科学家们创造生物系统人 一个稳定的状态,模型如图1所示。 工模型的原型。 经过不断的研究探索,Milford等提出一种基于 维视觉细胞” 链路编码 鼠类导航细胞的扩展海马模型RatSLAM,该模型包 视 括位姿细胞、视觉细胞以及经验图3部分,通过一维 觉 拓扑化的 经历图 E-<PVd 头方向细胞和二维位置细胞合并形成的三维位姿 联 4 细胞表征当前位置,利用一维视觉细胞在环境中学 习独特场景,通过位姿细胞和视觉细胞链路编码共 二维位姿细胞P 链路编码 同构建拓扑化的经验图,其经验E包含关于视觉细 胞V、位姿细胞P和位置间拓扑关系d,定义E=〈V, 图1 RatSLAM模型 P,d)o Fig.1 RatSLAM model
SOM),并引入赢者通吃(winner take all, WTA) 理 论,该仿生优化方法通过学习能够自主绘制出拓扑 地图,但需通过大量的尝试确定其初始网络结构, 无法保证系统的实时性能,研究者们基于该模型的 缺陷进行了改进。 1993 年 Martinetz 等[2] 提出一种 神经气(neural gas,NG)模型,提高了网络自组织学 习过程的效率。 2004 年尹峻松等[3] 为克服 SOM 孤 立学习与噪声敏感等缺陷, 结合一氧化氮(NO)扩 散机理, 在 SOM 网中引入时间增强机制,提出了一 种新型扩散的自组织模型( diffusing self⁃organizing maps,DSOM)。 2009 年王春东等[4] 将 SOM 理论运 用于 信 息 学, 利 用 灰 色 关 联 系 数 ( grey relational coefficient,GRC) 调 整 权 重, 检 测 拒 绝 服 务 攻 击 (denial of service, DOS)。 2011 年于乃功等[5] 将可 增 长 特 征 映 射 图 ( growing self⁃organizing map, GSOM)融入双目立体视觉,通过自组织拓扑结构避 免了传统 SOM 网需大量实验才能确定的初始网络 结构。 本文以 GSOM 神经网络模型为基础引入了 方向参数和特征参数构成的动态增长自组织特征 图 ( dynamic growing self⁃organizing feature map, DGSOM),并应用于澳大利亚 Milford 等[6-9] 提出的 RatSLAM 模型中。 1 RatSLAM 模型 由于传感器和环境的不确定性,移动机器人利 用概率解决同步定位与地图构建问题。 其中,卡尔 曼滤波、极大期望估计和粒子滤波 3 种概率算法是 当前移动机器人 SLAM 的核心技术,其通过专用网 格或拓扑地图的方式进行环境描述,这些研究成果 在仿真和限定条件下能够取得良好效果,但难以兼 顾实际环境,且存在计算量大、搜索时间长、易于陷 入局部最优解等问题。 鼠类是生物医学研究最多的动物之一[10-11] ,人 们对于其导航、环境探索和真实神经机制的模拟理 解得很好,因此鼠类成为科学家们创造生物系统人 工模型的原型。 经过不断的研究探索,Milford 等提出一种基于 鼠类导航细胞的扩展海马模型 RatSLAM,该模型包 括位姿细胞、视觉细胞以及经验图 3 部分,通过一维 头方向细胞和二维位置细胞合并形成的三维位姿 细胞表征当前位置,利用一维视觉细胞在环境中学 习独特场景,通过位姿细胞和视觉细胞链路编码共 同构建拓扑化的经验图,其经验 E 包含关于视觉细 胞 V、位姿细胞 P 和位置间拓扑关系 d,定义 E = 〈V, P,d〉。 1.1 位姿细胞的活性状态变化 创建的兴奋度权重矩阵 εabc和由于兴奋性使位 姿感知细胞活动产生的变化 ΔPx′y′θ′ 如式( 1) 和式 (2)所示: εabc = 1 kx′y′ 2pkq′ ε - (a 2+b 2) k x′y′ ε - c 2 k θ′ (1) ΔPx′y′θ′ = ∑ Nx′ a = 0 ∑ Ny′ b = 0 ∑ Nθ′ c = 0 ε(a-x′)(b-y′)(c-θ′)Pabc - φ (2) 式中:kx′y′和 kθ′分别为位姿感知细胞平面( x′,y′)和 θ′维中对应着兴奋性一维分布的方差常数;a、b、c 分 别为 x′、y′、θ′的分布系数;Nx′、Ny′、Nθ′分别为(x′,y′, θ′)空间中的位姿感知细胞三维矩阵元素;抑制常数 φ 控制全局抑制水平,使兴奋度被限制在非负范 围内。 1.2 视觉细胞的场景学习及位姿关联 一维视觉细胞通过视觉关联影响位姿细胞活 性状态,其连接强度 a t+1 ix′y′θ′如式(3)所示: a t+1 ix′y′θ′ = {a t i,Px′y′θ′,Vi} (3) 视觉细胞关联下的位姿细胞网络活性如式(4) 所示: ΔPx′y′θ′ = δ∑i aix′y′θ′Vi (4) 式中 δ 为视觉校准加强常数。 1.3 经历图的构建 经验 E、编码位姿细胞 P、视觉细胞 V 和经历间 的拓扑关系 d 如式(5)所示: E = {P,V,d} (5) 拓扑关系 d 如式(6)所示: Δdi = α[∑ Nf j = 1 (dj - di - ΔPij) + ∑ Nt k = 1 (dk - di - ΔPkj)] (6) 式中:α 为学习常量;Nf 是从经历 i 到其他经历的转 移个数;Nt 是从其他经历到经历 i 的转移个数。 实 验表明,学习常量 α 取 0.5 可使构建的地图收敛到 一个稳定的状态,模型如图 1 所示。 图 1 RatSLAM 模型 Fig.1 RatSLAM model ·406· 智 能 系 统 学 报 第 12 卷

第3期 许瞳,等:一种融合DGSOM神经网络的仿生算法研究 .407. 2 DGSOM算法下的RatSLAM模型 2)计算权值向量与输入的距离 在第k个输入平面中,到每一个神经元i的 神经科学研究表明,视觉皮层与其海马脑区的 距离d,可由已知的m个神经元计算得出,可选取的 细胞存在竞争性输入[2-],而传统的SOM算 方法包括曼哈顿距离、欧氏距离、径向基等,这里采 法[14-]为确定初始网络结构需进行大量复杂的运 用输入样本与获胜神经元连接强度的欧氏距离进 算。本文提出一种具有神经元方向和特征的 行判断,计算方法如式(9)和式(10)所示: DGSOM神经网络模型,通过引入方向参数减少学习 次数从而降低系统的复杂度,通过引人特征参数避 d=e-m (9) 免感知混淆,将该模型应用于RatSLAM模型中以改 dn=min(d:) (10) 进现有基于鼠类海马体导航机制的细胞导航模型。 3)获取最佳匹配单元 方向参数D决定了RatSLAM模型中视觉细胞 通过引入阈值参数α选择是否需引入新的神 和位姿细胞的激活特性,激活值m和my取1,0, 经元,获取最佳匹配单元的数学模型,如式(11) -1。特征参数F决定了RatSLAM模型中视觉细胞 所示: 和位姿细胞的环境特征,其特征可分别表达为及 [0,i为已引入的神经元 ny,输入参数C可表达为c=mn和c=my d=1- i为已引入的神经元,且do<a ny,其中上标k表示第k个平面。 1 视觉细胞特征如式(7)所示: i为新引入的神经元,且dm≥a [n,m=1 (11) 4)调节神经元的权重 c=0, m=0 (7) 新引入的神经元如式(12)所示: -n m=-1 w'=c奇 (12) 位姿细胞特征如式(8)所示: 已引入的神经元如式(13)所示: (ny, my =1 (+B(c-),j=argmin d c=0, m=0 (8) w1= (w,其他 (-niy, my=-1 (13) 1)创建DGSOM网络 引入输入神经元C=〈D,F),DGSOM模型神经 式中:B=B。eP,B。赋初值0.1,p为允许在神经单元i 元的创建过程如图2所示,其中第3个神经元是竞 处创建的新节点数目:权重满足约束条件‖ω‖≤1。 5)构建一个新的神经元 争出的胜者,第m+1个神经元是新产生的神经元。 通过移动机器人在环境中探索,重复过程1)~ 4),构建一个新的神经元。 6)将DGSOM模型应用于RatSLAM 77 DGSOM下的RatSLAM模型如图3所示。通过 第k个输人平面的第个 神经元的特性表征 摄像头获取局部场景,利用视觉里程计信息整合至 m+1 CD,F 位姿细胞从而影响经历图的构建:融合DGSOM神 图2 DGSOM模型神经元的创建过程 经网络模型的视觉细胞,一方面对位姿细胞进行视 Fig.2 Neurons created in DGSOM model 觉关联,另一方面直接影响经历图的构建
2 DGSOM 算法下的 RatSLAM 模型 神经科学研究表明,视觉皮层与其海马脑区的 细胞 存 在 竞 争 性 输 入[12-13] , 而 传 统 的 SOM 算 法[14-19]为确定初始网络结构需进行大量复杂的运 算。 本 文 提 出 一 种 具 有 神 经 元 方 向 和 特 征 的 DGSOM 神经网络模型,通过引入方向参数减少学习 次数从而降低系统的复杂度,通过引入特征参数避 免感知混淆,将该模型应用于 RatSLAM 模型中以改 进现有基于鼠类海马体导航机制的细胞导航模型。 方向参数 D 决定了 RatSLAM 模型中视觉细胞 和位姿细胞的激活特性,激活值 m k i 和 m k x′y′取 1,0, -1。 特征参数 F 决定了 RatSLAM 模型中视觉细胞 和位姿细胞的环境特征,其特征可分别表达为 n k i 及 n k x′y′,输入参数 C 可表达为 c k i = m k i n k i 和 c k x′y′ = m k x′y′ n k x′y′,其中上标 k 表示第 k 个平面。 视觉细胞特征如式(7)所示: c k i = n k i , m k i = 1 0, m k i = 0 - n k i , m k i = - 1 ì î í ï ï ï ï (7) 位姿细胞特征如式(8)所示: c k x′y′ = n k x′y′, m k x′y′ = 1 0, m k x′y′ = 0 - n k x′y′, m k x′y′ = - 1 ì î í ï ï ï ï (8) 1) 创建 DGSOM 网络 引入输入神经元 C = 〈D,F〉,DGSOM 模型神经 元的创建过程如图 2 所示,其中第 3 个神经元是竞 争出的胜者,第 m+1 个神经元是新产生的神经元。 图 2 DGSOM 模型神经元的创建过程 Fig.2 Neurons created in DGSOM model 2)计算权值向量与输入的距离 在第 k 个输入 v k 平面中,到每一个神经元 i 的 距离 di 可由已知的 m 个神经元计算得出,可选取的 方法包括曼哈顿距离、欧氏距离、径向基等,这里采 用输入样本与获胜神经元连接强度的欧氏距离进 行判断,计算方法如式(9)和式(10)所示: di = ∑ m i = 1 (ci k - ωij) 2 [ ] 1 2 (9) dmin = min(di) (10) 3)获取最佳匹配单元 通过引入阈值参数 α 选择是否需引入新的神 经元,获取最佳匹配单元的数学模型,如式( 11) 所示: di = 0, i 为已引入的神经元 1 - dmin α , i 为已引入的神经元,且 dmin < α 1, i 为新引入的神经元,且 dmin ≥ α ì î í ï ï ï ï ïï (11) 4) 调节神经元的权重 新引入的神经元如式(12)所示: ω t+1 ij = c k ij (12) 已引入的神经元如式(13)所示: ω t+1 ij = ω t ij + β t (c k ij - ω t ij), j = argmin dj ω t ij, 其他 { (13) 式中:β t =β0 e - Ni ρ ,β0 赋初值 0.1,ρ 为允许在神经单元 i 处创建的新节点数目;权重满足约束条件‖ωij‖≤1。 5) 构建一个新的神经元 通过移动机器人在环境中探索,重复过程 1) ~ 4),构建一个新的神经元。 6) 将 DGSOM 模型应用于 RatSLAM DGSOM 下的 RatSLAM 模型如图 3 所示。 通过 摄像头获取局部场景,利用视觉里程计信息整合至 位姿细胞从而影响经历图的构建;融合 DGSOM 神 经网络模型的视觉细胞,一方面对位姿细胞进行视 觉关联,另一方面直接影响经历图的构建。 第 3 期 许曈,等:一种融合 DGSOM 神经网络的仿生算法研究 ·407·
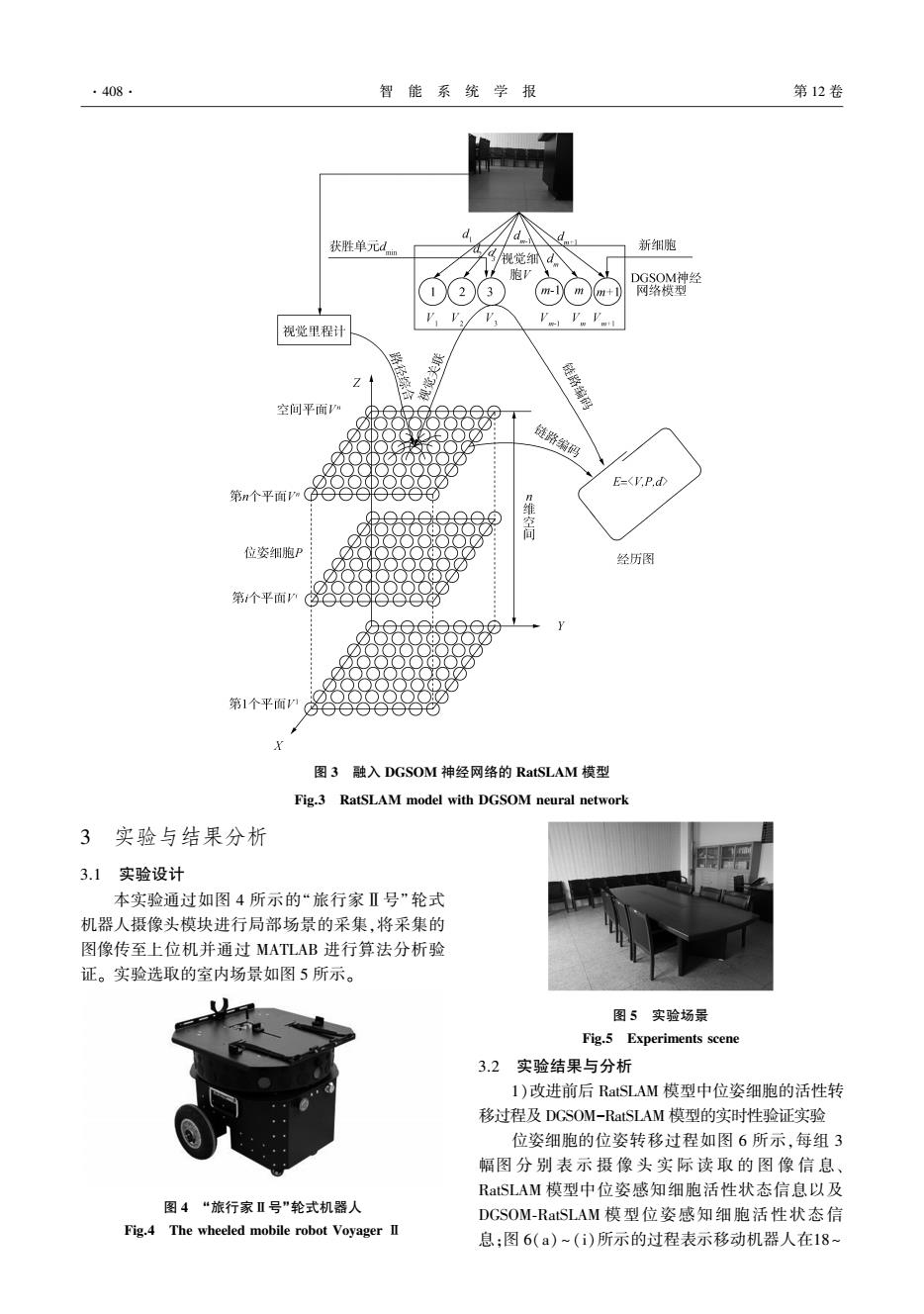
.408. 智能系统学报 第12卷 获胜单元dm 新细胞 视觉细d 止胞V DGSOM神经 1X23 m-m)m+) 网络模型 视觉里程计 Z 链路编码 空间平面V 链路编码 E= 第n个平面mOO 维 位姿细胞P 经历图 第个平面 第1个平面尖 图3融入DGSOM神经网络的RatSLAM模型 Fig.3 RatSLAM model with DGSOM neural network 3 实验与结果分析 3.1实验设计 本实验通过如图4所示的“旅行家Ⅱ号”轮式 机器人摄像头模块进行局部场景的采集,将采集的 图像传至上位机并通过MATLAB进行算法分析验 证。实验选取的室内场景如图5所示。 图5实验场景 Fig.5 Experiments scene 3.2实验结果与分析 1)改进前后RatSLAM模型中位姿细胞的活性转 移过程及DGSOM-RatSLAM模型的实时性验证实验 位姿细胞的位姿转移过程如图6所示,每组3 幅图分别表示摄像头实际读取的图像信息、 RatSLAM模型中位姿感知细胞活性状态信息以及 图4“旅行家Ⅱ号”"轮式机器人 DGSOM-RatSLAM模型位姿感知细胞活性状态信 Fig.4 The wheeled mobile robot Voyager II 息:图6(a)~(i)所示的过程表示移动机器人在18~
图 3 融入 DGSOM 神经网络的 RatSLAM 模型 Fig.3 RatSLAM model with DGSOM neural network 3 实验与结果分析 3.1 实验设计 本实验通过如图 4 所示的“旅行家Ⅱ号” 轮式 机器人摄像头模块进行局部场景的采集,将采集的 图像传至上位机并通过 MATLAB 进行算法分析验 证。 实验选取的室内场景如图 5 所示。 图 4 “旅行家Ⅱ号”轮式机器人 Fig.4 The wheeled mobile robot Voyager Ⅱ 图 5 实验场景 Fig.5 Experiments scene 3.2 实验结果与分析 1)改进前后 RatSLAM 模型中位姿细胞的活性转 移过程及 DGSOM-RatSLAM 模型的实时性验证实验 位姿细胞的位姿转移过程如图 6 所示,每组 3 幅图 分 别 表 示 摄 像 头 实 际 读 取 的 图 像 信 息、 RatSLAM 模型中位姿感知细胞活性状态信息以及 DGSOM⁃RatSLAM 模型位姿感知细胞活性状态信 息;图 6(a) ~ (i)所示的过程表示移动机器人在18~ ·408· 智 能 系 统 学 报 第 12 卷
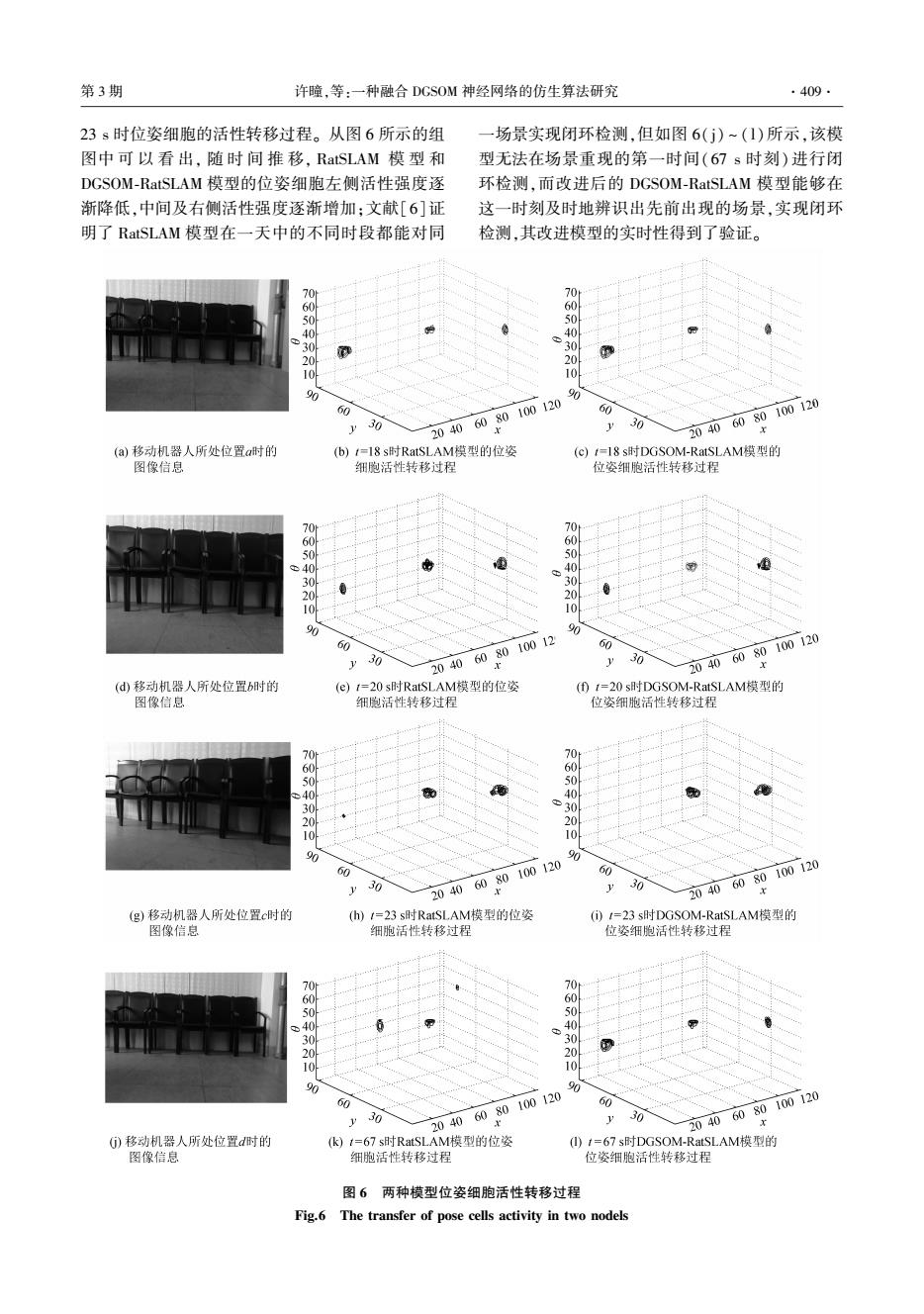
第3期 许瞳,等:一种融合DGSOM神经网络的仿生算法研究 ·409· 23s时位姿细胞的活性转移过程。从图6所示的组 一场景实现闭环检测,但如图6(j)~(1)所示,该模 图中可以看出,随时间推移,RatSLAM模型和 型无法在场景重现的第一时间(67s时刻)进行闭 DGSOM-RatSLAM模型的位姿细胞左侧活性强度逐 环检测,而改进后的DGSOM-RatSLAM模型能够在 渐降低,中间及右侧活性强度逐渐增加:文献[6]证 这一时刻及时地辨识出先前出现的场景,实现闭环 明了RatSLAM模型在一天中的不同时段都能对同 检测,其改进模型的实时性得到了验证。 8 81 0 公 20 90 60 60 y30 2040600 00120 30 20406080100120 (a)移动机器人所处位置时的 (b)1=18s时RatSLAM模型的位姿 (c)t-18s时DGSOM-RatSLAM模型的 图像信总 细胞活性转移过程 位姿细胞活性转移过程 60 40 28 0 3 20 10 90 90 60 0012 60 y 30 2040 6080 30 20406080100120 (d移动机器人所处位置b时的 (e)1=20s时RatSLAM模型的位姿 (D1=20s时DGSOM-RatSL.AM模型的 图像信息 细胞活性转移过程 位姿细胞活性转移过程 70 70t 50 40 4 28 10 0 0 60 20406080100120 60 y 3o 30 2040 6080100120 (g)移动机器人所处位置c时的 (h)t=23s时RatSLAM模型的位姿 ()t=23s时DGSOM-RatSLAM模型的 图像信息 细胞活性转移过程 位姿细胞活性转移过程 70 8 4 3 10 90 90 60 60 30 20406080100120 30 20406080100120 1 0)移动机器人所处位置d时的 (k)t=67s时RatSLAM模型的位姿 )t=67s时DGSOM-RatSLAM模型的 图像信息 细胞活性转移过程 位姿细胞活性转移过程 图6两种模型位姿细胞活性转移过程 Fig.6 The transfer of pose cells activity in two nodels
23 s 时位姿细胞的活性转移过程。 从图 6 所示的组 图中 可 以 看 出, 随 时 间 推 移, RatSLAM 模 型 和 DGSOM⁃RatSLAM 模型的位姿细胞左侧活性强度逐 渐降低,中间及右侧活性强度逐渐增加;文献[6]证 明了 RatSLAM 模型在一天中的不同时段都能对同 一场景实现闭环检测,但如图 6(j) ~ ( l)所示,该模 型无法在场景重现的第一时间(67 s 时刻) 进行闭 环检测,而改进后的 DGSOM⁃RatSLAM 模型能够在 这一时刻及时地辨识出先前出现的场景,实现闭环 检测,其改进模型的实时性得到了验证。 图 6 两种模型位姿细胞活性转移过程 Fig.6 The transfer of pose cells activity in two nodels 第 3 期 许曈,等:一种融合 DGSOM 神经网络的仿生算法研究 ·409·

·410 智能系统学报 第12卷 2)RatSLAM模型与DGSOM-RatSLAM模型的定 TP (15) 性分析 R=TP+FN RatSLAM模型与融入DGSOM神经网络的 a2+1 PR F。= (16) RatSLAM模型的性能对比如图7所示,相比于现有 a2P+R 的RatSLAM模型,DGSOM-RatSLAM模型采集相同 式中:正阳性(true positive,TP)指正确识别的闭环 场景时所需视觉细胞的个数更少,能够更快地进行 经验节点单元,假阳性(false positive,FP)指错误检 场景重定位且匹配效果更佳。 测出的闭环经验节点单元,假阴性(false negative, 700 FN)指未检测到的真实闭环经验节点单元,这里取 场景重现 600 区域 a=1,有 500 DGSOM+RatSLAM 2PR 400 RatSLAM F=P+R (17) 300 经计算,RatSLAM算法和DGSOM-RatSLAM算 200 法的准确率P分别为93.26%和94.74%,差异性不 100 显著:但相比于RatSLAM模型,DGSOM-RatSLAM模 20 4060 100 tis 型的召回率R有显著的提升,其中,RatSLAM算法 的召回率R仅为75.28%,即该算法在场景重定位中 图7 RatSLAM模型与DGSOM-RatSLAM模型性能对比 会导致较多的假阴性判断,DGSOM-RatSLAM算法 Fig.7 Performance comparison between RatSLAM and DGSOM-RatSLAM 的召回率R改进至86.88%,两种模型的F1值分别 为83.31%与90.64%,可以看出,DGS0M-RatSLAM 3)高斯噪声干扰下的RatSLAM模型与 DGSOM-RatSLAM模型的定性分析 算法性能得到了一定的改进,数据对比如表1所示。 表1 RatSLAM模型与DGSOM-RatSLAM模型性能对比 为进一步验证DGSOM-RatSLAM模型的有效 Tablel Performance comparison between RatSLAM 性,给所需处理的图像添加随机高斯噪声,其中正 model and DGSOM-RatSLAM model % 态分布的均值4取0,标准差σ取随机值[0.02, 模型 召回率R F,值 0.08]。高斯噪声干扰下的RatSLAM模型与 准确率P RatSLAM 93.26 DGSOM-RatSLAM模型性能对比如图8所示,相比 75.28 83.31 于RatSLAM模型,DGSOM-RatSLAM模型采集相同 DGSOM-RatSLAM 94.74 86.88 90.64% 场景时所需视觉细胞的个数更少,能够更快地实现 在每一帧图像中加入高斯噪声,得出其改进前后 闭环且匹配效果更佳。 的Gauss-RatSLAM模型及Gauss-DGSOM-RatSLAM,其 700 场景重现 准确率P分别为91.42%和86.70%,召回率R分别为 600 区域 71.33%和80.25%,计算得F,值分别为80.14%和 ← 500 Gauss-DGSOM-RatSLAM 83.35%,数据如表2所示。 400 Gauss-RatSLAM 表2 Gauss-RatSLAM模型与Gauss-DGSOM-RatSLAM 300 模型性能对比 200 Table 2 Performance comparison between Gauss-RatSLAM 100 model and Gauss-DGSOM-RatSLAM model % 20 40 60 80 100 模型 准确率P召回率RF,值 tis Gauss-RatSLAM 91.42 71.33 80.14 图8 Gauss-.RatSLAM模型与Gauss-.DGSOM-RatSLAM 模型性能对比 Gauss-DGSOM-RatSLAM 86.70 80.25 83.35 Fig.8 Performance comparison between Gauss-RatSLAM 对比两模型的准确率、召回率及F,值可以看 and Gauss-DGSOM-RatSLAM 出,融入DGSOM的鼠类导航细胞模型整体性能得 4)准确率与召回率对闭环检测的定量分析 到了一定的改进。 引入准确率P、召回率R及F值对两种系统进 5)实验场景匹配效果对比 行评估,数学模型如式(14)~(16)所示: RatSLAM模型与融入DGSOM神经网络的 TP RatSLAM模型的实验场景匹配效果对比如图9所 P=- (14) TP FP 示,DGSOM-RatSLAM模型在闭环匹配中具有更好
2)RatSLAM 模型与 DGSOM⁃RatSLAM 模型的定 性分析 RatSLAM 模 型 与 融 入 DGSOM 神 经 网 络 的 RatSLAM 模型的性能对比如图 7 所示,相比于现有 的 RatSLAM 模型,DGSOM⁃RatSLAM 模型采集相同 场景时所需视觉细胞的个数更少,能够更快地进行 场景重定位且匹配效果更佳。 图 7 RatSLAM 模型与 DGSOM⁃RatSLAM 模型性能对比 Fig.7 Performance comparison between RatSLAM and DGSOM⁃RatSLAM 3) 高 斯 噪 声 干 扰 下 的 RatSLAM 模 型 与 DGSOM⁃RatSLAM 模型的定性分析 为进一步验证 DGSOM⁃RatSLAM 模型的有效 性,给所需处理的图像添加随机高斯噪声,其中正 态分布的均值 μ 取 0,标准差 σ 取随机值[ 0. 02, 0.08]。 高 斯 噪 声 干 扰 下 的 RatSLAM 模 型 与 DGSOM⁃RatSLAM 模型性能对比如图 8 所示,相比 于 RatSLAM 模型,DGSOM⁃RatSLAM 模型采集相同 场景时所需视觉细胞的个数更少,能够更快地实现 闭环且匹配效果更佳。 图 8 Gauss⁃RatSLAM 模型与 Gauss⁃DGSOM⁃RatSLAM 模型性能对比 Fig.8 Performance comparison between Gauss⁃RatSLAM and Gauss⁃DGSOM⁃RatSLAM 4)准确率与召回率对闭环检测的定量分析 引入准确率 P、召回率 R 及 F 值对两种系统进 行评估,数学模型如式(14) ~ (16)所示: P = TP TP + FP (14) R = TP TP + FN (15) Fa = a 2 + 1 a 2 PR P + R (16) 式中:正阳性( true positive,TP) 指正确识别的闭环 经验节点单元,假阳性(false positive,FP)指错误检 测出的闭环经验节点单元,假阴性( false negative, FN)指未检测到的真实闭环经验节点单元,这里取 a = 1,有 F1 = 2PR P + R (17) 经计算,RatSLAM 算法和 DGSOM⁃RatSLAM 算 法的准确率 P 分别为 93.26%和 94.74%,差异性不 显著;但相比于 RatSLAM 模型,DGSOM⁃RatSLAM 模 型的召回率 R 有显著的提升,其中,RatSLAM 算法 的召回率 R 仅为 75.28%,即该算法在场景重定位中 会导致较多的假阴性判断,DGSOM⁃RatSLAM 算法 的召回率 R 改进至 86.88%,两种模型的 F1 值分别 为 83.31% 与 90. 64%,可以看出,DGSOM⁃RatSLAM 算法性能得到了一定的改进,数据对比如表 1 所示。 表 1 RatSLAM 模型与 DGSOM⁃RatSLAM 模型性能对比 Table1 Performance comparison between RatSLAM model and DGSOM⁃RatSLAM model % 模型 准确率 P 召回率 R F1 值 RatSLAM 93.26 75.28 83.31 DGSOM⁃RatSLAM 94.74 86.88 90.64% 在每一帧图像中加入高斯噪声,得出其改进前后 的 Gauss⁃RatSLAM 模型及 Gauss⁃DGSOM⁃RatSLAM,其 准确率 P 分别为 91.42%和 86.70%,召回率 R 分别为 71.33% 和 80. 25%,计算得 F1 值分别为 80. 14% 和 83.35%,数据如表 2 所示。 表 2 Gauss⁃RatSLAM 模型与 Gauss⁃DGSOM⁃RatSLAM 模型性能对比 Table 2 Performance comparison between Gauss⁃RatSLAM model and Gauss⁃DGSOM⁃RatSLAM model % 模型 准确率 P 召回率 R F1 值 Gauss⁃RatSLAM 91.42 71.33 80.14 Gauss⁃DGSOM⁃RatSLAM 86.70 80.25 83.35 对比两模型的准确率、召回率及 F1 值可以看 出,融入 DGSOM 的鼠类导航细胞模型整体性能得 到了一定的改进。 5)实验场景匹配效果对比 RatSLAM 模 型 与 融 入 DGSOM 神 经 网 络 的 RatSLAM 模型的实验场景匹配效果对比如图 9 所 示,DGSOM⁃RatSLAM 模型在闭环匹配中具有更好 ·410· 智 能 系 统 学 报 第 12 卷

第3期 许瞳,等:一种融合DGSOM神经网络的仿生算法研究 411 的鲁棒性和快速性。 主地图构建方法[J].计算机测量与控制,2011,19 -30 (11):2810-2813 -31 一段时间内 检测到 YU Naigong,WANG Li.Autonomous mapping for robot -32 未成功闭环 闭环 -33 -RatSLAM using a combination of binocular stereo vision and GSOM -34 -DGSOM-RatSLAM [J].Computer measurement and control,2011,19(11): 实际闭环 2810-2813. -36 成功闭环发生位置 -37 [6]MILFORD M,GEORGE A.Featureless visual processing for -38 -39 SLAM in changing outdoor environments[J].Springer tracts -40 in advanced robotics,2014:569-583. 48 -45 42 -39-36-33 x/m [7]MILFORD M J,PRASSER D P,WYETH G F.Effect 图9 RatSLAM模型与DGSOM-RatSLAM模型实验 ofrepresentation size and visual ambiguity on RatSLAM 场景匹配效果对比 system performance[C]//Australasian Conference on Robotics Fig.9 Matching effect of experiment scene between and Automation.Australian Robotics and Automation Society RatSLAM and DGSOM-RatSLAM (ARAA),2006:1-8. [8 MILFORD M,SCHULZ R,PRASSER D,et al. 4 结束语 learningspatial concepts from RatSLAM representations[J]. Robotics and autonomous systems,2007,55(5):403-410. 与现有的RatSLAM模型相比,本文提出的 [9]MILFORD M,WYETH G.PRASSER D.RatSLAM on the DGSOM-RatSLAM模型将DGSOM神经网络融入视 edge:revealing a coherent representation from an 觉细胞,通过减少所需细胞的数量降低了系统的复 overloaded rat brain [C1//leee/rsi International 杂度,并且通过位姿细胞活性状态实验与视觉细胞 Conference on Intelligent Robots and Systems,IROS 2006. 实验分别验证了DGSOM-RatSLAM模型能够更早地 0 ctober9-15,2006,Beijing,China.2006:4060-4065. 匹配到闭环,使系统具有更好的快速性能,优化了 [10]王丽娟,陶璨,张光伟,等.小鼠初级听皮层S0M中间神 匹配效果,其准确率、召回率及F,值与传统 经元突触输入的时空特性研究[J].第三军医大学学 RatSLAM模型相比有一定的改进,分别达94.74%、 报,2017,39(5):417-422. WANG Lijuan,TAO Can,ZHANG Guangwei,et al. 86.88%和90.64%,进一步进行鲁棒性测试可知融入 Spatial-temporal characteristics of synaptic inputs received 高斯噪声干扰下的改进模型的准确率、召回率及F, by SOM+interneurons in mouse primary auditory cortex 值分别达86.70%、80.25%、83.35%。 [J].Journal of third military medical university,2017,39 参考文献: (5):417-422. [11]于乃功,方略,罗子维,等大鼠脑海马结构认知机理及 [1]KOHONEN T.Self-organized formation of topologically 其在机器人导航中的应用[J]北京工业大学学报, correct feature maps[]]Biological cybernetics,1982.43 2017,43(3):434-442. (1):59-69. YU Naigong,FANG Lue,LUO Ziwei,et al.Cognitive [2]MARTINETZ T M,BERKOVICH S G.SCHULTEN K J. mechanism of rat hippocampal formation and its application Neural-gas network for vector quantization and its in robot navigation[J].Journal of Beijing university of application to time-series prediction[J].IEEE transactions technology,2017,43(3):434-442. on neural networks,1993,4(4):558-569. [12]刘帅师,程曦,郭文燕,等.深度学习方法研究新进展 [3]尹峻松,胡德文,陈爽,等.DSOM:一种基于NO时空动 [J].智能系统学报,2016,11(5):567-577. 态扩散机理的新型自组织模型[J].中国科学E辑:信息 LIU Shuaishi,CHENG Xi,GUO Wenyan,et al.Progress 科学,2004,34(10):1094-1109. report on new research in deep learning [J].CAAI YIN Junsong,HU Dewen,CHEN Shuang,et al.DSOM:a transactions on intelligent systems,2016,11 (5): new self-organization model based on NO space-time 567-577. dynamic diffusion mechanism[J].Science in China ser.E [13]丁永生.计算智能的新框架:生物网络结构[J].智能系 information sciences,2004,34(10):1094-1109 统学报,2007,2(2):26-30. [4]王春东,虞鹤峰,王怀彬.Grey self--organizing map based DING Yongsheng.A new scheme for computational intrusion detection [J].Optoelectronics letters,2009,5 intelligence:bio-network architecture [J].CAAl (1):64-68. transactions on intelligent systems,2007,2(2):26-30. [5]于乃功,王丽双目立体视觉和GSOM相结合的机器人自 [14]芮小平,张立强.基于S0M的多维信息可视化研究[J]
的鲁棒性和快速性。 图 9 RatSLAM 模型与 DGSOM⁃RatSLAM 模型实验 场景匹配效果对比 Fig.9 Matching effect of experiment scene between RatSLAM and DGSOM⁃RatSLAM 4 结束语 与现 有 的 RatSLAM 模 型 相 比, 本 文 提 出 的 DGSOM⁃RatSLAM 模型将 DGSOM 神经网络融入视 觉细胞,通过减少所需细胞的数量降低了系统的复 杂度,并且通过位姿细胞活性状态实验与视觉细胞 实验分别验证了 DGSOM⁃RatSLAM 模型能够更早地 匹配到闭环,使系统具有更好的快速性能,优化了 匹配 效 果, 其 准 确 率、 召 回 率 及 F1 值 与 传 统 RatSLAM 模型相比有一定的改进,分别达 94.74%、 86.88%和 90.64%,进一步进行鲁棒性测试可知融入 高斯噪声干扰下的改进模型的准确率、召回率及 F1 值分别达 86.70%、80.25%、83.35%。 参考文献: [ 1 ] KOHONEN T. Self⁃organized formation of topologically correct feature maps[J]. Biological cybernetics, 1982, 43 (1): 59-69. [2] MARTINETZ T M, BERKOVICH S G, SCHULTEN K J. Neural⁃gas network for vector quantization and its application to time⁃series prediction[J]. IEEE transactions on neural networks, 1993,4(4): 558-569. [3]尹峻松, 胡德文, 陈爽,等. DSOM:一种基于 NO 时空动 态扩散机理的新型自组织模型[ J].中国科学 E 辑:信息 科学,2004,34(10): 1094-1109. YIN Junsong, HU Dewen, CHEN Shuang, et al. DSOM: a new self⁃organization model based on NO space⁃time dynamic diffusion mechanism[ J]. Science in China ser. E information sciences, 2004,34(10): 1094-1109. [4]王春东, 虞鹤峰, 王怀彬. Grey self⁃organizing map based intrusion detection [ J ]. Optoelectronics letters, 2009, 5 (1): 64-68. [5]于乃功,王丽.双目立体视觉和 GSOM 相结合的机器人自 主地图构建方法 [ J]. 计算机测量与控制, 2011, 19 (11): 2810-2813. YU Naigong, WANG Li. Autonomous mapping for robot using a combination of binocular stereo vision and GSOM [J]. Computer measurement and control, 2011, 19( 11): 2810-2813. [6]MILFORD M, GEORGE A. Featureless visual processing for SLAM in changing outdoor environments[J]. Springer tracts in advanced robotics, 2014: 569-583. [7] MILFORD M J, PRASSER D P, WYETH G F. Effect ofrepresentation size and visual ambiguity on RatSLAM system performance[C] / / Australasian Conference on Robotics and Automation. Australian Robotics and Automation Society (ARAA), 2006: 1-8. [ 8 ] MILFORD M, SCHULZ R, PRASSER D, et al. learningspatial concepts from RatSLAM representations[ J]. Robotics and autonomous systems, 2007, 55(5):403-410. [9]MILFORD M, WYETH G, PRASSER D. RatSLAM on the edge: revealing a coherent representation from an overloaded rat brain [ C ] / / Ieee / rsj International Conference on Intelligent Robots and Systems, IROS 2006, October 9-15, 2006, Beijing, China. 2006:4060-4065. [10]王丽娟,陶璨,张光伟,等.小鼠初级听皮层 SOM 中间神 经元突触输入的时空特性研究[ J]. 第三军医大学学 报, 2017, 39(5): 417-422. WANG Lijuan, TAO Can, ZHANG Guangwei, et al. Spatial⁃temporal characteristics of synaptic inputs received by SOM + interneurons in mouse primary auditory cortex [J]. Journal of third military medical university, 2017,39 (5): 417-422. [11]于乃功,方略,罗子维,等.大鼠脑海马结构认知机理及 其在机器人导航中的应用[ J]. 北京工业大学学报, 2017, 43(3): 434-442. YU Naigong, FANG Lue, LUO Ziwei, et al. Cognitive mechanism of rat hippocampal formation and its application in robot navigation [ J ]. Journal of Beijing university of technology, 2017, 43(3): 434-442. [12]刘帅师, 程曦, 郭文燕,等. 深度学习方法研究新进展 [J]. 智能系统学报, 2016, 11(5):567-577. LIU Shuaishi, CHENG Xi, GUO Wenyan,et al. Progress report on new research in deep learning [ J ]. CAAI transactions on intelligent systems, 2016, 11 ( 5 ): 567-577. [13]丁永生.计算智能的新框架:生物网络结构[ J]. 智能系 统学报, 2007, 2(2): 26-30. DING Yongsheng. A new scheme for computational intelligence: bio⁃network architecture [ J ]. CAAI transactions on intelligent systems, 2007, 2(2): 26-30. [14]芮小平,张立强.基于 SOM 的多维信息可视化研究[ J]. 第 3 期 许曈,等:一种融合 DGSOM 神经网络的仿生算法研究 ·411·

·412 智能系统学报 第12卷 应用基础与工程科学学报,2011,19(3):379-388 [19]赵建华,李伟华.有监督S0M神经网络在入侵检测中 RUI Xiaoping,ZHANG Liqiang.Multi-dimensional information 的应用J].计算机工程,2012,38(12):110-111. visualization based on SOM[J].Joumal of basic science and ZHAO Jianhua,LI Weihua.Application of supervised SOM engineering,2011,19(3):379-388 neural network in intrusion detection [J].Computer [15]尹柏强,何怡刚,朱彦卿.一种广义S变换及模糊S0M engineer,.2012,38(12):110-111 网络的电能质量多扰动检测和识别方法[].中国电机 作者简介: 工程学报,2015,35(4):866-872. 许瞳,男,1993年生,硕士研究生 YIN baiqiang,HE Yigang,ZHU Yanqing.Detection and 主要研究方向为机器视觉和仿生导航 classification of power quality multi-disturbances based on generalized S-transform and fuzzy SOM neural network[J]. 算法。 Proceedings of the CSEE,2015,35(4):866-872. [I6]於东军,吴小俊,HANCOCK Edwin R,等.广义SOM及 其在人脸性别识别中的应用[J].计算机学报,2011,34 (9):1719-1725 YU Dongjun,WU Xiaojun,HANCOCK Edwin R,et al. 凌有铸,男,1962年生,研究生导 Generalized SOM with application to facial gender 师,主要研究方向为传感器信号处理和 identification[J].Chinese journal of computers,2011,34 机器人地图构建等。主持省自然科学 (9):1719-1725. 基金、省科技计划项目等10余项,获安 [17]刘艳,陈丽安.基于SOM的真空断路器机械故障诊断 徽省科学技术奖4项,发表学术论文60 [J].电工技术学报,2017.32(5):49-54 余篇。 LIU Yan,CHEN Li'an.Mechanical fault diagnosis of vacuum circuit breaker based on SOM[J].Transactions of 陈孟元,男,1984年生,副教授,主 China electrotechnical society,2017,32(5):49-54. 要研究方向为移动机器人地图构建及 [18]邱天宇,申富饶,赵金熙.自组织增量学习神经网络综 同步定位等。主持安徽省高等学校自 述[J].软件学报,2016.27(9):2230-2247. 然科学研究项目等10余项,发表学术 QIU Tianyu,SHEN Furao,ZHAO Jinxi.Review of self- organizing incremental neural network [J].Journal of 论文30余篇,授权国家发明专利4项。 software,2016,27(9):2230-2247
应用基础与工程科学学报, 2011, 19(3): 379-388. RUI Xiaoping, ZHANG Liqiang. Multi⁃dimensional information visualization based on SOM[J]. Journal of basic science and engineering, 2011, 19(3): 379-388. [15]尹柏强,何怡刚,朱彦卿.一种广义 S 变换及模糊 SOM 网络的电能质量多扰动检测和识别方法[ J].中国电机 工程学报, 2015, 35(4): 866-872. YIN baiqiang, HE Yigang, ZHU Yanqing. Detection and classification of power quality multi⁃disturbances based on generalized S⁃transform and fuzzy SOM neural network[J]. Proceedings of the CSEE,2015,35(4):866-872. [16]於东军,吴小俊, HANCOCK Edwin R,等.广义 SOM 及 其在人脸性别识别中的应用[J].计算机学报, 2011, 34 (9): 1719-1725. YU Dongjun, WU Xiaojun, HANCOCK Edwin R, et al. Generalized SOM with application to facial gender identification[ J].Chinese journal of computers, 2011, 34 (9): 1719-1725. [17] 刘艳,陈丽安.基于 SOM 的真空断路器机械故障诊断 [J].电工技术学报, 2017,32(5):49-54. LIU Yan, CHEN Li’ an. Mechanical fault diagnosis of vacuum circuit breaker based on SOM[J]. Transactions of China electrotechnical society, 2017, 32(5): 49-54. [18]邱天宇, 申富饶, 赵金熙. 自组织增量学习神经网络综 述[J]. 软件学报, 2016, 27(9): 2230-2247. QIU Tianyu, SHEN Furao, ZHAO Jinxi. Review of self⁃ organizing incremental neural network [ J ]. Journal of software, 2016, 27(9): 2230-2247 [19]赵建华, 李伟华. 有监督 SOM 神经网络在入侵检测中 的应用[J]. 计算机工程, 2012, 38(12): 110-111. ZHAO Jianhua, LI Weihua. Application of supervised SOM neural network in intrusion detection [ J ]. Computer engineer, 2012, 38(12): 110-111. 作者简介: 许曈,男,1993 年生,硕士研究生, 主要研究方向为机器视觉和仿生导航 算法。 凌有铸,男,1962 年生,研究生导 师,主要研究方向为传感器信号处理和 机器人地图构建等。 主持省自然科学 基金、省科技计划项目等 10 余项,获安 徽省科学技术奖 4 项,发表学术论文 60 余篇。 陈孟元,男,1984 年生,副教授,主 要研究方向为移动机器人地图构建及 同步定位等。 主持安徽省高等学校自 然科学研究项目等 10 余项,发表学术 论文 30 余篇,授权国家发明专利 4 项。 ·412· 智 能 系 统 学 报 第 12 卷