
第12卷第5期 智能系统学报 Vol.12 No.5 2017年10月 CAAI Transactions on Intelligent Systems 0ct.2017 D0I:10.11992/is.201706033 网络出版地址:htp:/kns.cmki.net/kcms/detail/23.1538.TP.20170831.1058.018.html 基于Spark的多标签超网络集成学习 李航,王进2,赵蕊2 (1.重庆邮电大学软件工程学院,重庆400065:2.重庆邮电大学计算智能重庆市重点实验室,重庆400065) 摘要:近年来,多标签学习在图像识别和文本分类等多个领域得到了广泛关注,具有越来越重要的潜在应用价值。 尽管多标签学习的发展日新月异,但仍然存在两个主要挑战,即如何利用标签间的相关性以及如何处理大规模的多 标签数据。针对上述问题,基于MLHN算法,提出一种能有效利用标签相关性且能处理大数据集的基于Sak的多 标签超网络集成算法SE-MLHN。该算法首先引人代价敏感,使其适应不平衡数据集。其次,改良了超网络演化学 习过程,并优化了损失函数,降低了算法时间复杂度。最后,进行了选择性集成,使其适应大规模数据集。在11个不 同规模的数据集上进行实验,结果表明,该算法具有较好的分类性能,较低的时间复杂度且具备良好的处理大规模 数据集的能力。 关键词:多标签学习;超网络:标签相关性;Apache Spark;选择性集成学习 中图分类号:TP181文献标志码:A文章编号:1673-4785(2017)05-0624-16 中文引用格式:李航,王进,赵蕊.基于Spark的多标签超网络集成学习[J].智能系统学报,2017,12(5):624-639. 英文引用格式:LI Hang,WANG Jin,ZHAO Rui.Multi-label hypernetwork ensemble learning based on Spark[J].CAAI transactions on intelligent systems,2017,12(5):624-639. Multi-label hypernetwork ensemble learning based on Spark LI Hang',WANG Jin2,ZHAO Rui2 (1.College of Software Engineering,Chongqing University of Posts and Telecommunications,Chongqing 400065,China;2.Chongqing Key Laboratory of Computational Intelligence,Chongging University of Posts and Telecommunications,Chongging 400065,China) Abstract:Multi-label learning has attracted a great deal of attention in recent years and has a wide range of potential real-world applications,including image identification and text categorization.Although great effort has been expended in the development of multi-label learning,two main challenges remain,i.e.,how to utilize the correlation between labels and how to tackle large-scale multi-label data.To solve these challenges,based on the multi-label hypernetwork (MLHN)algorithm,in this paper,we propose a Spark-based multi-label hypernetwork ensemble algorithm(SEI-MLHN)that effectively utilizes label correlation and can deal with large-scale multi-label datasets.First,the algorithm introduces cost sensitivity to enable it to adapt to unbalanced datasets.Secondly,it improves the hypernetwork evolution learning process,optimizes the loss function,and reduces the inherent time complexity.Lastly,it uses selective ensemble learning to enable it to adapt to large-scale datasets.We conducted experiments on 11 datasets wit different scales.The results show that the proposed algorithm demonstrates excellent categorization performance,low time complexity,and the capability to handle large-scale datasets. Keywords:multi-label learning;hypernetwork;label correlations;Apache Spark;selective ensemble learning 多标签学习在文本分类】、图像注释[3]和生有越来越重要的应用价值。在多标签学习中,训练 物信息学)等多个应用领域得到了广泛关注,也具 集的一个样本均对应一组标签集合。假设X表示 样本空间,Y={1,2,…,9}表示所有可能的标签集 收稿日期:2017-06-09.网络出版日期:2017-08-31. 合,其中标签的总数为q,T={(x1,Y),(x2,Y2),, 基金项目:重庆市基础与前沿研究计划项目(cstc2014 jeyiA40001, cstc2014 jcyjA40022):重庆教委科学技术研究项目(自然科 (xm,Ym)}为具有m个样本的训练集,其中x:∈X且 学类)(K1400436). Y二Y。则多标签分类的目标是输出一个多标签分 通信作者:李航.E-mail:1326202954@q4.com
第 12 卷第 5 期 智 能 系 统 学 报 Vol.12 №.5 2017 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2017 DOI:10.11992 / tis.201706033 网络出版地址:http: / / kns.cnki.net / kcms/ detail / 23.1538.TP.20170831.1058.018.html 基于 Spark 的多标签超网络集成学习 李航1 ,王进2 ,赵蕊2 (1.重庆邮电大学 软件工程学院,重庆 400065; 2. 重庆邮电大学 计算智能重庆市重点实验室,重庆 400065) 摘 要:近年来,多标签学习在图像识别和文本分类等多个领域得到了广泛关注,具有越来越重要的潜在应用价值。 尽管多标签学习的发展日新月异,但仍然存在两个主要挑战,即如何利用标签间的相关性以及如何处理大规模的多 标签数据。 针对上述问题,基于 MLHN 算法,提出一种能有效利用标签相关性且能处理大数据集的基于 Spark 的多 标签超网络集成算法 SEI-MLHN。 该算法首先引入代价敏感,使其适应不平衡数据集。 其次,改良了超网络演化学 习过程,并优化了损失函数,降低了算法时间复杂度。 最后,进行了选择性集成,使其适应大规模数据集。 在 11 个不 同规模的数据集上进行实验,结果表明,该算法具有较好的分类性能,较低的时间复杂度且具备良好的处理大规模 数据集的能力。 关键词:多标签学习;超网络;标签相关性;Apache Spark;选择性集成学习 中图分类号:TP181 文献标志码:A 文章编号:1673-4785(2017)05-0624-16 中文引用格式:李航,王进,赵蕊.基于 Spark 的多标签超网络集成学习[J]. 智能系统学报, 2017, 12(5): 624-639. 英文引用 格 式: LI Hang, WANG Jin, ZHAO Rui. Multi⁃label hypernetwork ensemble learning based on Spark [ J ]. CAAI transactions on intelligent systems, 2017, 12(5): 624-639. Multi⁃label hypernetwork ensemble learning based on Spark LI Hang 1 , WANG Jin 2 , ZHAO Rui 2 (1.College of Software Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China; 2. Chongqing Key Laboratory of Computational Intelligence, Chongqing University of Posts and Telecommunications, Chongqing 400065, China) Abstract:Multi⁃label learning has attracted a great deal of attention in recent years and has a wide range of potential real⁃world applications, including image identification and text categorization. Although great effort has been expended in the development of multi⁃label learning, two main challenges remain, i. e., how to utilize the correlation between labels and how to tackle large⁃scale multi⁃label data. To solve these challenges, based on the multi⁃label hypernetwork (MLHN) algorithm, in this paper, we propose a Spark⁃based multi⁃label hypernetwork ensemble algorithm (SEI⁃MLHN) that effectively utilizes label correlation and can deal with large⁃scale multi⁃label datasets. First, the algorithm introduces cost sensitivity to enable it to adapt to unbalanced datasets. Secondly, it improves the hypernetwork evolution learning process, optimizes the loss function, and reduces the inherent time complexity. Lastly, it uses selective ensemble learning to enable it to adapt to large⁃scale datasets. We conducted experiments on 11 datasets wit different scales. The results show that the proposed algorithm demonstrates excellent categorization performance, low time complexity, and the capability to handle large⁃scale datasets. Keywords:multi⁃label learning; hypernetwork; label correlations; Apache Spark; selective ensemble learning 收稿日期:2017-06-09. 网络出版日期:2017-08-31. 基金项 目: 重 庆 市 基 础 与 前 沿 研 究 计 划 项 目 ( cstc2014jcyjA40001, cstc2014jcyjA40022);重庆教委科学技术研究项目(自然科 学类)(KJ1400436). 通信作者:李航.E⁃mail:1326202954@ qq.com. 多标签学习在文本分类[1-2] 、图像注释[3-4]和生 物信息学[5]等多个应用领域得到了广泛关注,也具 有越来越重要的应用价值。 在多标签学习中,训练 集的一个样本均对应一组标签集合。 假设 X 表示 样本空间,Y = {1,2,…,q} 表示所有可能的标签集 合,其中标签的总数为 q,T = {(x1 ,Y1 ),(x2 ,Y2 ),…, (xm ,Ym )}为具有 m 个样本的训练集,其中 xi∈X 且 Yi⊆Y。 则多标签分类的目标是输出一个多标签分

第5期 李航,等:基于Spark的多标签超网络集成学习 ·625· 类器h:x→2',使得对每一个给定的实例x∈X,都能 据集,同时算法也未考虑到标签不平衡对性能的 预测出合适的标签集合Y·二Y。 影响。 多标签学习的关键挑战在于分类器预测的标 针对目前多标签超网络存在的问题,本文基于 签空间数量为指数级(2)。为了解决这个问题,有 MLHN的思想,提出了Spark平台下的改进多标签 效地利用不同标签之间的相关性以促进学习过程 超网络集成算法SEI-MLHN,有效且高效地解决了 已成为多标签学习的关键6-刃。在过去几年,许多 多标签学习问题。首先对多标签数据集进行划分: 利用标签相关性的算法被提出,如校准标签排序 然后对划分后的数据分别用基于Spark平台的改进 (CLR)[)⑧,随机k标签集(RAkEL)[)和广义k标签 超网络算法SI-MLHN进行训练,形成多个局部超网 集成(GLE)[均考虑了标签之间的相关性,然而这 络:最后对多个局部超网络进行选择性集成完成对 些算法的计算复杂度随标签数量的增加而显著 测试样本的预测。其中,SI-MLHN利用MLHN的思 增加。 想并在Spark平台下进行改进,首先计算每个样本 同时,大部分现有的多标签学习方法没有充分 的k近邻,然后利用k近邻对超网络进行演化学习, 考虑多标签数据的固有属性,即标签类别不平衡。 得到演化超网络。 对每一个标签y∈Y,令D={(x,+1)y∈Y:,1≤ 为了评估本文算法的性能以及对大规模数据 i≤N}以及D={(x:,-1)lyY:,1≤i≤N}作为正 集的适应性,选用不同规模数据集来进行对比实 样本和负样本。一般来说,每个类别的正训练样本 验,验证了本文算法具有良好性能以及具备处理大 数远远低于其负训练样本数,这可能导致大多数多 规模数据集的能力。本文的主要贡献如下: 标签学习算法的性能降低。文献[12-14]指出, 1)引入了代价敏感,使其能良好地适应多标签 不平衡问题普遍存在于多标签应用中,会损害分类 不平衡数据,提升算法性能; 性能。算法交叉耦合聚合学习方法(cross-coupling 2)改良了超网络演化学习过程,大幅度降低 aggregation,COCOA)[同时考虑了标签相关性和 MLHN算法的计算复杂度: 不平衡问题,同样其算法复杂度很高,因此如何有 3)利用选择性集成,降低了时间复杂度,并提 效和高效地利用标签间的相关性并削弱不平衡问 高分类性能; 题的影响仍然是一个悬而未决的问题。 4)基于Spark计算框架实现算法,使算法实现 另一方面,目前现实应用中的多标签数据集的 并行,提高算法运行效率。 样本、特征和标签的数量远远超过常规大小,例如, 1 相关工作 视频共享网站Youtube中有数百万个视频,而每个 视频可以被数百万个候选类别标记。然而,大多数 虽然多标签学习已经成功应用于生物信息学 多标签学习算法不能很好地适应数据集规模很大 音频分类[2]以及wb挖掘2]等多个领域,但是由 的应用。对近3年出现的多标签学习方法[5-]使 于多标签分类器的输出空间为指数级,以及现在大 用的训练集的规模进行统计,可以看出训练样本数 部分应用的数据集规模日益增加,对多标签学习造 在50000~100000之间的数据集仅有5个,样本数 成了很大的挑战。 大于100000的数据集仅有1个,大多数现有的多标 为了应对分类器输出空间数量巨大这个问题, 签学习算法仅适用于处理中小规模数据集。其次, 现有的方法是利用标签相关性来促进学习过程。 文献[19]虽然利用大规模数据集进行了实验,但是 基于标签关联性,张敏灵和周志华[7-]将现有的学 它的计算复杂度高。 习算法分为3类,分别为一阶策略、二阶策略以及高 多标签超网络LHN与协同演化多标签超网 阶策略。一阶策略是简单地将多标签学习转为多 络Co-MLHN[24]可以挖掘标签间的高阶关系,它将 个独立的二分类问题来解决多标签学习问题,例如 传统的超网络转为多标签超网络,用超边和超边的 L-KNN2]、BR[30]等:二阶策略通过利用标签之间 权重来表示特征子集与标签之间的高阶关系,利用 的成对关系解决多标签学习问题,例如CLR31] 了任意标签间的相关性,且计算复杂度随标签数量 BP-ML[)]等:高阶策略通过探索标签之间的高阶 的增加呈线性增长,但是其算法时间复杂度与样本 关系来解决多标签学习问题,例如CC[3)、CNMF[34] 数量呈平方级关系,不能很好地处理规模较大的数 等。对这3种策略进行比较分析,一阶策略的效率
类器 h:x→2 y ,使得对每一个给定的实例 x∈X,都能 预测出合适的标签集合 Y ∗⊆Y。 多标签学习的关键挑战在于分类器预测的标 签空间数量为指数级(2 q )。 为了解决这个问题,有 效地利用不同标签之间的相关性以促进学习过程 已成为多标签学习的关键[6-7] 。 在过去几年,许多 利用标签相关性的算法被提出,如校准标签排序 (CLR) [8] ,随机 k 标签集(RAkEL) [9] 和广义 k 标签 集成(GLE) [10]均考虑了标签之间的相关性,然而这 些算法的计算复杂度随标签数量的增加而显著 增加。 同时,大部分现有的多标签学习方法没有充分 考虑多标签数据的固有属性,即标签类别不平衡。 对每一个标签 yj∈Y,令 D + j = {(xi,+1) yj∈Yi,1≤ i≤N}以及 D - j = {(xi,-1) yj∉Yi,1≤i≤N}作为正 样本和负样本。 一般来说,每个类别的正训练样本 数远远低于其负训练样本数,这可能导致大多数多 标签学习算法的性能降低[11] 。 文献[12-14]指出, 不平衡问题普遍存在于多标签应用中,会损害分类 性能。 算法交叉耦合聚合学习方法( cross⁃coupling aggregation, COCOA) [14] 同时考虑了标签相关性和 不平衡问题,同样其算法复杂度很高,因此如何有 效和高效地利用标签间的相关性并削弱不平衡问 题的影响仍然是一个悬而未决的问题。 另一方面,目前现实应用中的多标签数据集的 样本、特征和标签的数量远远超过常规大小,例如, 视频共享网站 Youtube 中有数百万个视频,而每个 视频可以被数百万个候选类别标记。 然而,大多数 多标签学习算法不能很好地适应数据集规模很大 的应用。 对近 3 年出现的多标签学习方法[15-23] 使 用的训练集的规模进行统计,可以看出训练样本数 在50 000~100 000之间的数据集仅有 5 个,样本数 大于100 000的数据集仅有 1 个,大多数现有的多标 签学习算法仅适用于处理中小规模数据集。 其次, 文献[19]虽然利用大规模数据集进行了实验,但是 它的计算复杂度高。 多标签超网络 MLHN 与协同演化多标签超网 络 Co⁃MLHN [24]可以挖掘标签间的高阶关系,它将 传统的超网络转为多标签超网络,用超边和超边的 权重来表示特征子集与标签之间的高阶关系,利用 了任意标签间的相关性,且计算复杂度随标签数量 的增加呈线性增长,但是其算法时间复杂度与样本 数量呈平方级关系,不能很好地处理规模较大的数 据集,同时算法也未考虑到标签不平衡对性能的 影响。 针对目前多标签超网络存在的问题,本文基于 MLHN 的思想,提出了 Spark 平台下的改进多标签 超网络集成算法 SEI⁃MLHN,有效且高效地解决了 多标签学习问题。 首先对多标签数据集进行划分; 然后对划分后的数据分别用基于 Spark 平台的改进 超网络算法 SI⁃MLHN 进行训练,形成多个局部超网 络;最后对多个局部超网络进行选择性集成完成对 测试样本的预测。 其中,SI⁃MLHN 利用 MLHN 的思 想并在 Spark 平台下进行改进,首先计算每个样本 的 k 近邻,然后利用 k 近邻对超网络进行演化学习, 得到演化超网络。 为了评估本文算法的性能以及对大规模数据 集的适应性,选用不同规模数据集来进行对比实 验,验证了本文算法具有良好性能以及具备处理大 规模数据集的能力。 本文的主要贡献如下: 1)引入了代价敏感,使其能良好地适应多标签 不平衡数据,提升算法性能; 2)改良了超网络演化学习过程,大幅度降低 MLHN 算法的计算复杂度; 3)利用选择性集成,降低了时间复杂度,并提 高分类性能; 4)基于 Spark 计算框架实现算法,使算法实现 并行,提高算法运行效率。 1 相关工作 虽然多标签学习已经成功应用于生物信息学、 音频分类[25] 以及 web 挖掘[26] 等多个领域,但是由 于多标签分类器的输出空间为指数级,以及现在大 部分应用的数据集规模日益增加,对多标签学习造 成了很大的挑战。 为了应对分类器输出空间数量巨大这个问题, 现有的方法是利用标签相关性来促进学习过程。 基于标签关联性,张敏灵和周志华[27-28] 将现有的学 习算法分为 3 类,分别为一阶策略、二阶策略以及高 阶策略。 一阶策略是简单地将多标签学习转为多 个独立的二分类问题来解决多标签学习问题,例如 ML⁃KNN [29] 、BR [30] 等;二阶策略通过利用标签之间 的成对关系解决多标签学习问题,例如 CLR [31 ] 、 BP⁃MLL [32]等;高阶策略通过探索标签之间的高阶 关系来解决多标签学习问题,例如 CC [33] 、CNMF [34] 等。 对这 3 种策略进行比较分析,一阶策略的效率 第 5 期 李航,等:基于 Spark 的多标签超网络集成学习 ·625·

·626 智能系统学报 第12卷 高且概念易理解,但忽略了标签相关性。二阶策略 首先,对多标签数据集进行划分,然后对划分后的 在一定程度上解决了标签相关性,但忽略了现实世 数据分别用SI-MLHN算法进行训练,形成多个局部 界中相关性超过二阶的情况。高阶策略具有比一 超网络,最后对多个局部超网络进行选择性集成完 阶和二阶更强的建模能力,但是其计算复杂度更 成对测试样本的预测。其中,算法SI-MLHN利用 高,可扩展性更低。 MLHN的思想,在Spark平台下进行改进,首先计算 为了应对多标签数据的不平衡性造成算法 每个样本的k近邻,然后利用k近邻对超网络进行 性能下降这个问题,常规解决方案是为每一个标 演化学习,得到超网络。本节中,将对算法MLHN, 签训练一个二分类器,并通过随机或合成欠采 MLHN的改进算法SI-MLHN,以及以SI-MLHN为基 样/过采样来处理这个二分类器[35-6],但这些方 学习器进行选择性集成的算法SEI-MLHN依次进行 法没有很好地利用标签间的关联性。也有其他 介绍。 的解决方案,如张敏灵等[1)提出交叉耦合聚合 2.1 多标签演化超网络(MLHN)】 算法C0COA,但是这种算法时间复杂度高,不适 多标签演化超网络利用超边集合以及超边权 合处理大规模数据集。 重来表示样本特征子集与多标签类别之间的高阶 为了应对数据集规模大这个问题,现有的解决 关联。通过演化学习,可以近似地表示训练样本X 方案是利用分布式存储系统,提供一个基础架构, 和其标签Y之间的概率分布P(X,Y),在MLHN中 从而实现高效和可扩展的大数据挖掘与分析。目 可以按式(1)进行表示: 前,为大数据分析开发了大量的计算框架7),其 P(x,y:=1) 中,最经典的是MapReduce[。MapReduce简单 P(y:=1x) P(x) 通用且成熟,被广泛使用,但是它只能进行M即和 0x%=19 Reduce计算,不适合描述复杂数据处理过程,数据 需要写到磁盘,不能有效地执行迭代算法。为了克 ,0=19)+y,10x=09 服MapReduce的缺点,大量的计算框架被设计出 (1) 来,如Haloop【wy、Apache Mahout[),i2 MapReduce 式中:y:为样本x的第i个标签;0:为超边集合 [o]和Apache Spark[a】等。Haloop是Hadoop |E|中e,的第i个权重向量的值;I(x,y:;e)为超边 MapReduce框架的修改版本,它继承了Hadoop的基 与样本匹配函数,若匹配则取值为1,反之则为0,如 本分布式计算模型和架构。Apache Mahout是一个 式(2)所示: 开源项目,主要用于创建可扩展的机器学习算法。 (1,dis(xn;e)≤8且y元=ym I(x。,ym;e;)= i2 MapReduce是MapReduce的一个增量处理扩展, 0,其他 并广泛用于大数据挖掘。Apache Spark是一个开源 (2) 的集群计算框架,用于大规模的交互计算。在上述 式中:ya是超边e的第i个标签,dis(xn;e)为超边 框架中,Apache Spark利用内存计算,并保留 e,与样本x的欧氏距离,δ为匹配阈值。δ的计算方 MapReduce的可扩展性和容错能力,对迭代算法非 法如式(3): 常有效。Spark执行速度比Hadoop MapReduce快 dim(e) G.lx dim(l 6= (3) 100倍[),并且显著快于其他计算框架。 综上所述,为了解决上述问题,本文使用Spark 式中:其中G,为x的近邻样本集合,dim(x)为样本 计算框架作为平台来实现多标签算法。 x的特征维度。 为了对未知样本进行预测,MLHN通常把标签 2 Spark下改进多标签超网络集成 预测误差和相关标签不一致性最小化作为演化学 算法 习目标。通过超边初始化、超边替代和梯度下降演 MLHN可以高效地挖掘标签间的关联性且学习 化学习来对训练集进行学习,使超边权重心:进行更 复杂度与标签维度呈线性关系,因此本文基于 新,流程如图1所示。图1中,超边ea=(",y4, MLHN算法提出了Spark平台下的改进多标签超网 w6),'a是超边的顶点,为x的部分特征;y。为x的 络集成算法SEI-MLHN,高效地解决了多标签问题。 标签;w是x.对应y.的权重向量
高且概念易理解,但忽略了标签相关性。 二阶策略 在一定程度上解决了标签相关性,但忽略了现实世 界中相关性超过二阶的情况。 高阶策略具有比一 阶和二阶更强的建模能力,但是其计算复杂度更 高,可扩展性更低。 为了应对多标签数据的不平衡性造成算法 性能下降这个问题,常规解决方案是为每一个标 签训练一个二分类器,并通过随机 或 合 成 欠 采 样 / 过采样来处理这个二分类器[ 35-36] ,但这些方 法没有很好地利用标签间的关联性。 也有其他 的解决方案,如张敏灵等[ 14] 提出交叉耦合聚合 算法 COCOA,但是这种算法时间复杂度高,不适 合处理大规模数据集。 为了应对数据集规模大这个问题,现有的解决 方案是利用分布式存储系统,提供一个基础架构, 从而实现高效和可扩展的大数据挖掘与分析。 目 前,为大数据分析开发了大量的计算框架[37-41] ,其 中,最经典的是 MapReduce [37] 。 MapReduce 简单、 通用且成熟,被广泛使用,但是它只能进行 Map 和 Reduce 计算,不适合描述复杂数据处理过程,数据 需要写到磁盘,不能有效地执行迭代算法。 为了克 服 MapReduce 的缺点,大量的计算框架被设计出 来,如 Haloop [38] 、Apache Mahout [39] 、i2MapReduce [40]和 Apache Spark [41] 等。 Haloop 是 Hadoop MapReduce 框架的修改版本,它继承了 Hadoop 的基 本分布式计算模型和架构。 Apache Mahout 是一个 开源项目,主要用于创建可扩展的机器学习算法。 i2MapReduce 是 MapReduce 的一个增量处理扩展, 并广泛用于大数据挖掘。 Apache Spark 是一个开源 的集群计算框架,用于大规模的交互计算。 在上述 框架 中, Apache Spark 利 用 内 存 计 算, 并 保 留 MapReduce 的可扩展性和容错能力,对迭代算法非 常有效。 Spark 执行速度比 Hadoop MapReduce 快 100 倍 [41] ,并且显著快于其他计算框架。 综上所述,为了解决上述问题,本文使用 Spark 计算框架作为平台来实现多标签算法。 2 Spark 下改进多标签超网络集成 算法 MLHN 可以高效地挖掘标签间的关联性且学习 复杂度 与 标 签 维 度 呈 线 性 关 系, 因 此 本 文 基 于 MLHN 算法提出了 Spark 平台下的改进多标签超网 络集成算法 SEI⁃MLHN,高效地解决了多标签问题。 首先,对多标签数据集进行划分,然后对划分后的 数据分别用 SI⁃MLHN 算法进行训练,形成多个局部 超网络,最后对多个局部超网络进行选择性集成完 成对测试样本的预测。 其中,算法 SI⁃MLHN 利用 MLHN 的思想,在 Spark 平台下进行改进,首先计算 每个样本的 k 近邻,然后利用 k 近邻对超网络进行 演化学习,得到超网络。 本节中,将对算法 MLHN, MLHN 的改进算法 SI⁃MLHN,以及以 SI⁃MLHN 为基 学习器进行选择性集成的算法 SEI⁃MLHN 依次进行 介绍。 2.1 多标签演化超网络(MLHN) 多标签演化超网络利用超边集合以及超边权 重来表示样本特征子集与多标签类别之间的高阶 关联。 通过演化学习,可以近似地表示训练样本 X 和其标签 Y 之间的概率分布 P(X,Y),在 MLHN 中 可以按式(1)进行表示: P(yi = 1 x) = P(x,yi = 1) P(x) = ∑ E j = 1 wji I(x,yi = 1;ej) ∑ E j = 1 wji I(x,yi = 1;ej) + ∑ E j = 1 wji I(x,yi = 0;ej) (1) 式中: yi 为样本 x 的第 i 个标签;wji 为超边集合 E 中 ej 的第 i 个权重向量的值;I(x,yi;ej)为超边 与样本匹配函数,若匹配则取值为 1,反之则为 0,如 式(2)所示: I(xn ,yni;ej) = 1, dis(xn ;ej) ≤ δ 且 yji = yni {0, 其他 (2) 式中:yji是超边 ej 的第 i 个标签, dis(xn ;ej) 为超边 ej 与样本 x 的欧氏距离,δ 为匹配阈值。 δ 的计算方 法如式(3): δ = dim(ej) Gx × dim(x)∑x′∈Gx ‖x - x′‖ (3) 式中:其中 Gx 为 x 的近邻样本集合,dim(x)为样本 x 的特征维度。 为了对未知样本进行预测,MLHN 通常把标签 预测误差和相关标签不一致性最小化作为演化学 习目标。 通过超边初始化、超边替代和梯度下降演 化学习来对训练集进行学习,使超边权重 wji进行更 新,流程如图 1 所示。 图 1 中,超边 eh = ( vh , yh , wh ),vh 是超边的顶点,为 x 的部分特征;yh 为 x 的 标签;wh 是 xh 对应 yh 的权重向量。 ·626· 智 能 系 统 学 报 第 12 卷
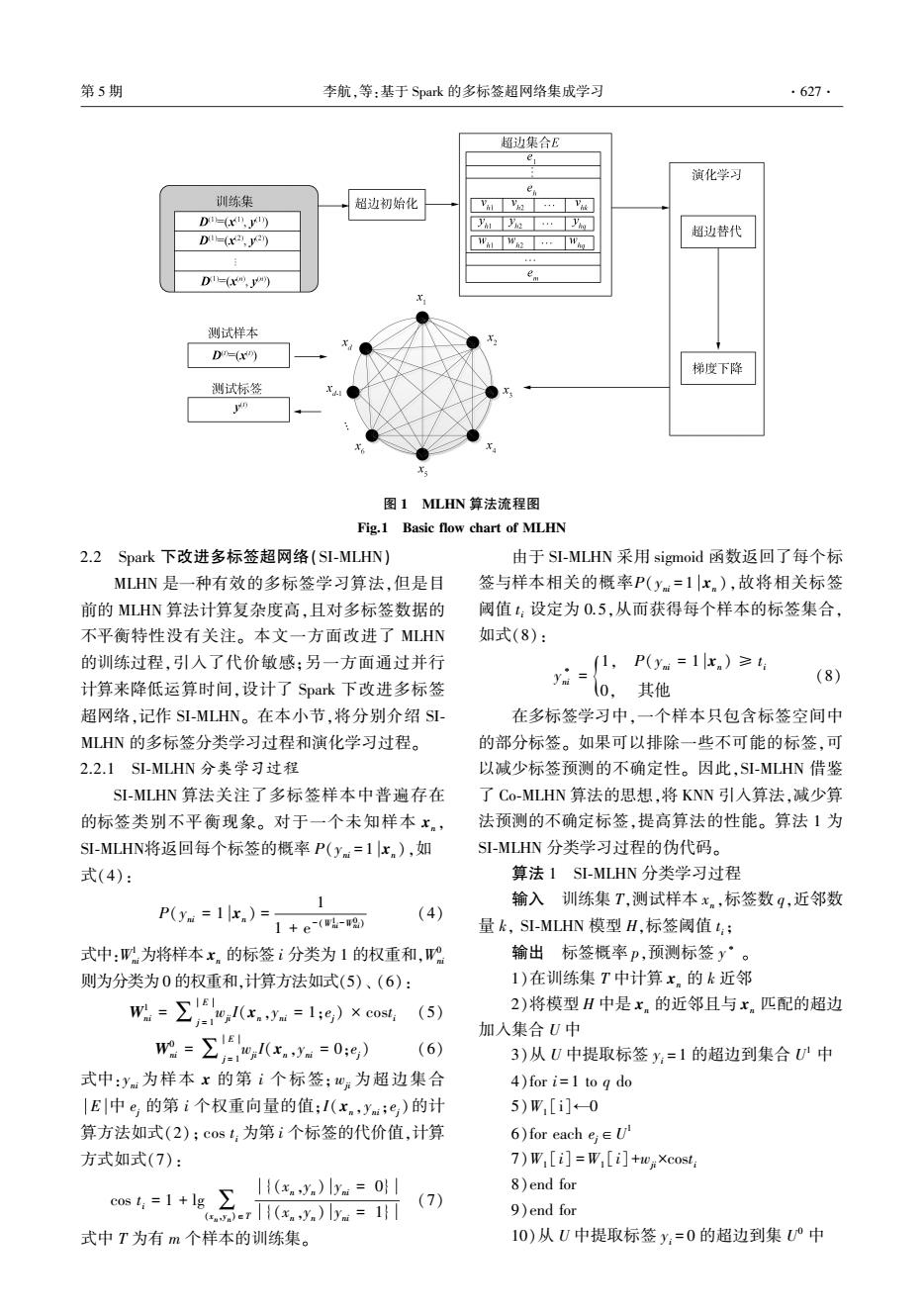
第5期 李航,等:基于Spark的多标签超网络集成学习 ·627. 超边集合E e 演化学习 e 训练集 超边初始化 VilVh2.Vis D(x) Y12·y 超边替代 D=(2,y2 W1w2…w D1=(xm,) 测试样本 D=(x) 梯度下降 测试标签 J” 图1MLHN算法流程图 Fig.1 Basic flow chart of MLHN 2.2 Spark下改进多标签超网络(Sl-MLHN) 由于SL-MLHN采用sigmoid函数返回了每个标 MLHN是一种有效的多标签学习算法,但是目 签与样本相关的概率P(ym=1x.),故将相关标签 前的MLHN算法计算复杂度高,且对多标签数据的 阈值:设定为0.5,从而获得每个样本的标签集合, 不平衡特性没有关注。本文一方面改进了MLHN 如式(8): 的训练过程,引入了代价敏感:另一方面通过并行 1,P(ym=1xn)≥ y= (8) 计算来降低运算时间,设计了Spark下改进多标签 0,其他 超网络,记作SI-MLHN。在本小节,将分别介绍SL 在多标签学习中,一个样本只包含标签空间中 MLHN的多标签分类学习过程和演化学习过程。 的部分标签。如果可以排除一些不可能的标签,可 2.2.1SI-MLHN分类学习过程 以减少标签预测的不确定性。因此,SI-MLHN借鉴 S-MLHN算法关注了多标签样本中普遍存在 了Co-MLHN算法的思想,将KNN引入算法,减少算 的标签类别不平衡现象。对于一个未知样本x。, 法预测的不确定标签,提高算法的性能。算法1为 SI-MLHN将返回每个标签的概率P(ym=1x),如 SI-MLHN分类学习过程的伪代码。 式(4): 算法1SI-MLHN分类学习过程 P(m=1x)=1 输入训练集T,测试样本x。,标签数q,近邻数 1+e(h-8) (4) 量k,SI-MLHN模型H,标签阈值t: 式中:W为将样本x。的标签i分类为1的权重和,W 输出标签概率p,预测标签y·。 则为分类为0的权重和,计算方法如式(5)、(6): 1)在训练集T中计算x。的k近邻 w=∑,10xa=1g)×c(5) 2)将模型H中是x.的近邻且与x匹配的超边 加入集合U中 明=,0x=05) (6) 3)从U中提取标签y:=1的超边到集合U中 式中:y为样本x的第i个标签;w:为超边集合 4)for i=1 to q do |E中e,的第i个权重向量的值;I(x.,ym;e)的计 5)W[i]←0 算方法如式(2);cost:为第i个标签的代价值,计算 6)for each e∈U 方式如式(7): 7)W,[i]=W,[i]+w元×cost (x)y=o 8)end for w4=1+器2 (7) 9)end for 式中T为有m个样本的训练集。 10)从中提取标签y,=0的超边到集°中
图 1 MLHN 算法流程图 Fig.1 Basic flow chart of MLHN 2.2 Spark 下改进多标签超网络(SI⁃MLHN) MLHN 是一种有效的多标签学习算法,但是目 前的 MLHN 算法计算复杂度高,且对多标签数据的 不平衡特性没有关注。 本文一方面改进了 MLHN 的训练过程,引入了代价敏感;另一方面通过并行 计算来降低运算时间,设计了 Spark 下改进多标签 超网络,记作 SI⁃MLHN。 在本小节,将分别介绍 SI⁃ MLHN 的多标签分类学习过程和演化学习过程。 2.2.1 SI⁃MLHN 分类学习过程 SI⁃MLHN 算法关注了多标签样本中普遍存在 的标签类别不平衡现象。 对于一个未知样本 xn , SI⁃MLHN将返回每个标签的概率 P(yni = 1 xn ),如 式(4): P(yni = 1 xn ) = 1 1 + e -(W1 ni -W0 ni ) (4) 式中:W 1 ni为将样本 xn 的标签 i 分类为 1 的权重和,W 0 ni 则为分类为 0 的权重和,计算方法如式(5)、 (6): W 1 ni = ∑ E j = 1 wji I(xn ,yni = 1;ej) × cost i (5) W 0 ni = ∑ E j = 1 wji I(xn ,yni = 0;ej) (6) 式中:yni 为样本 x 的第 i 个标签; wji 为超边集合 E 中 ej 的第 i 个权重向量的值;I( xn ,yni;ej)的计 算方法如式(2); cos t i 为第 i 个标签的代价值,计算 方式如式(7): cos t i = 1 + lg ∑ (xn ,yn )∈T {(xn ,yn ) yni = 0} {(xn ,yn ) yni = 1} (7) 式中 T 为有 m 个样本的训练集。 由于 SI⁃MLHN 采用 sigmoid 函数返回了每个标 签与样本相关的概率P(yni = 1 xn ),故将相关标签 阈值 t i 设定为 0.5,从而获得每个样本的标签集合, 如式(8): y ∗ ni = 1, P(yni = 1 xn ) ≥ t i 0, 其他 { (8) 在多标签学习中,一个样本只包含标签空间中 的部分标签。 如果可以排除一些不可能的标签,可 以减少标签预测的不确定性。 因此,SI⁃MLHN 借鉴 了 Co⁃MLHN 算法的思想,将 KNN 引入算法,减少算 法预测的不确定标签,提高算法的性能。 算法 1 为 SI⁃MLHN 分类学习过程的伪代码。 算法 1 SI⁃MLHN 分类学习过程 输入 训练集 T,测试样本 xn ,标签数 q,近邻数 量 k, SI⁃MLHN 模型 H,标签阈值 t i; 输出 标签概率 p,预测标签 y ∗ 。 1)在训练集 T 中计算 xn 的 k 近邻 2)将模型 H 中是 xn 的近邻且与 xn 匹配的超边 加入集合 U 中 3)从 U 中提取标签 yi = 1 的超边到集合 U 1 中 4)for i = 1 to q do 5)W1 [i]←0 6)for each ej∈U 1 7)W1 [i] =W1 [i]+wji ×cost i 8)end for 9)end for 10)从 U 中提取标签 yi = 0 的超边到集 U 0 中 第 5 期 李航,等:基于 Spark 的多标签超网络集成学习 ·627·

·628 智能系统学报 第12卷 11)for i=1 to q do 度越高,则适应值越高。同时,式(4)也展示出,样 12)W[i]←0 本与匹配超边的标签相似度越高,被正确分类的概 l3)for each e∈ 率越大。 14)W[i门=W[]+0月 本文将预测误差作为学习目标。损失函数如 15)end for 式(10)所示,P·(ym=1x.)为SI-MLHN分类器对 16)end for 样本(xmyn)的第i个标签的预测值,利用梯度下降 17)for i=1 to g do 调整超边的权重,降低损失值。超边权重更新为式 1 (11),并通过式(12)~(14),计算△0,其中心为 18)P(y:=1x.)=1+em-a可 第k条超边第i个标签的权重,)为学习速率。 19)p[i]=P(y:=1lxn) (网=2[P6.=小)-P.=1k 20)ifP(ym=1x.)≥t (10) 21)y·[i]=1 0后=10:+△10 (11) 22)else y·[i]=0 aErr,(W) 23)end if △10a=-7 (12) oWki 24)end for Err,(W) 25)return p,y' aw =(P(y=1x)- 2.2.2SI-MLHN演化学习过程 SI-MLHN利用超边的顶点和权重向量来代表 P*(y=1x)) ap'(y:=1x) (13) 8wki 多标签数据标签间的高阶关联,其权重向量由超边 1 从训练集中演化学习而来,首先进行了超边初始 ap'(yni=1x)1+e-(w-w&) 化,然后进行了超边替代与梯度下降演化学习,并 8w 利用Spark进行分布式并行计算,通过多个操作技 1 巧,如cache、broadst,.将变量缓存于内存中,大量减 1- 1+e-(w-w9 少了网络交换数据量和磁盘/0操作,使算法更 1+e-(-9) (14) 高效。 算法2为SI-MLHN的演化学习流程伪代码。 在超边初始化的过程中,利用样本(x,y)生成 由于本文采用欧氏距离作为距离度量,故需要先进 超边e=(v,,w),超边的顶点向量v随机地从样本 行归一化处理。 x特征中产生,标签向量)为样本的标签y,权重向 算法2SI-MLHN演化学习算法 量初始化为1,表示为w=[w102…0,],其中:= 输入训练集T={(xn,yn)}(1≤n≤N),标签 1.0(1≤i≤q)。 数q,每个样本生成的超边数e,超边替代迭代次数 由于超边顶点向量为随机的,为了更好地拟 t,随机梯度下降迭代次数ta,样本的近邻数量k: 合训练样本,需要通过超边替代来选择适应度高的 输出SI-MLHN:H。 超边。如果新生成的超边适应值高于现有超边,则 1)To=T.map 替换该超边。适应值的计算方法如式(9)所示: 2)每条样本进行归一化 fites(eg)=a2,q白 Σ1立1.=1(9) 3)end map.cache 4)T Bro broadcast(Tor) 式中:超边e的近邻样本个数为k,G为与超边e匹 5)Tky=Thor .map 配的抽样训练集TS样本集合,则将TS中样本的数 6)每条样本计算与TBo中样本的欧式距离 量设置为10倍的k,其中k个是超边e,的近邻样 7)end map.map 本,其余的样本则为训练集样本的随机抽样;9为标 8)获取距离最近的k个样本 签数量;ym为样本(xn,yn)的第i个标签;y:'为超边 9)end map e,的第i个标签。由式(9)可以看出适应值代表了 10)Ti,Bro broadcast(Tv) 超边标签与匹配样本标签的相似度的平均值,相似 ll)Hm=T,.flatmap
11)for i = 1 to q do 12) W0 [i]←0 13) for each ej∈U 0 14) W0 [i] =W0 [i]+wji 15) end for 16)end for 17)for i = 1 to q do 18) P(yi = 1 xn )= 1 1+e -(W1 [i]-W0 [i]) 19)p[i] =P(yi = 1 xn ) 20) if P(yni = 1 xn )≥t i 21)y ∗ [i] = 1 22)else y ∗ [i] = 0 23)end if 24)end for 25)return p,y ∗ 2.2.2 SI⁃MLHN 演化学习过程 SI⁃MLHN 利用超边的顶点和权重向量来代表 多标签数据标签间的高阶关联,其权重向量由超边 从训练集中演化学习而来,首先进行了超边初始 化,然后进行了超边替代与梯度下降演化学习,并 利用 Spark 进行分布式并行计算,通过多个操作技 巧,如 cache、broadst,将变量缓存于内存中,大量减 少了网络交换数据量和磁盘 I/ O 操作,使算法更 高效。 在超边初始化的过程中,利用样本( x,y) 生成 超边 e = (v,y ^ ,w),超边的顶点向量 v 随机地从样本 x 特征中产生,标签向量 y ^ 为样本的标签 y,权重向 量初始化为 1,表示为 w = [w1 w2… wq],其中wi = 1.0(1≤i≤q)。 由于超边顶点向量 v 为随机的,为了更好地拟 合训练样本,需要通过超边替代来选择适应度高的 超边。 如果新生成的超边适应值高于现有超边,则 替换该超边。 适应值的计算方法如式(9)所示: fitness(ej) = 1 G ∑ (xn ,yn ) 1 q ∑ q i = 1 i yni = yi { ′} (9) 式中:超边 ej 的近邻样本个数为 k,G 为与超边 ej 匹 配的抽样训练集 TS 样本集合,则将 TS 中样本的数 量设置为 10 倍的 k,其中 k 个是超边 ej 的近邻样 本,其余的样本则为训练集样本的随机抽样;q 为标 签数量;yni为样本(xn ,yn )的第 i 个标签;yi ′为超边 ej 的第 i 个标签。 由式(9)可以看出适应值代表了 超边标签与匹配样本标签的相似度的平均值,相似 度越高,则适应值越高。 同时,式(4) 也展示出,样 本与匹配超边的标签相似度越高,被正确分类的概 率越大。 本文将预测误差作为学习目标。 损失函数如 式(10)所示,P ∗ ( yni = 1 xn ) 为 SI⁃MLHN 分类器对 样本(xn ,yn )的第 i 个标签的预测值,利用梯度下降 调整超边的权重,降低损失值。 超边权重更新为式 (11),并通过式(12) ~ (14),计算 Δwki,其中 wki为 第 k 条超边第 i 个标签的权重,η 为学习速率。 Errn(W) = 1 2∑ q i = 1 [P ∗ (yni = 1 xn) - P(yni = 1 xn)] 2 (10) wki = wki + Δwki (11) Δwki = - η ∂Errn(W) ∂wki (12) ∂Errn(W) ∂wki = (P(yni = 1 xn ) - P ∗ (yni = 1 xn )) ∂P ∗ (yni = 1 xn ) ∂wki (13) ∂P ∗ (yni = 1 xn ) ∂wki = ∂ 1 1 + e -(W1 ni -W0 ni ) ∂wki = 1 - 1 1 + e -(W1 ni -W0 ni ) 1 + e -(W1 ni -W0 ni ) (14) 算法 2 为 SI⁃MLHN 的演化学习流程伪代码。 由于本文采用欧氏距离作为距离度量,故需要先进 行归一化处理。 算法 2 SI⁃MLHN 演化学习算法 输入 训练集 T = {(xn ,yn )} (1≤n≤N),标签 数 q,每个样本生成的超边数 e, 超边替代迭代次数 t r,随机梯度下降迭代次数 t d ,样本的近邻数量 k; 输出 SI⁃MLHN:H。 1) Tnor = T .map 2)每条样本进行归一化 3) end map.cache 4) TnorBro = broadcast( Tnor ) 5) Tkv = Tnor .map 6)每条样本计算与 TnorBro 中样本的欧式距离 7)end map.map 8)获取距离最近的 k 个样本 9)end map 10) TkvBro = broadcast( Tkv ) 11) Hini = Tkv .flatmap ·628· 智 能 系 统 学 报 第 12 卷

第5期 李航,等:基于Spark的多标签超网络集成学习 ·629 12)每条样本生成e条超边 区计算获胜节点,并更新优胜邻域中的输出单元, 13)end flatmap.cache 然后将各个分区的值利用reduce算子进行合并,并 14)Ho=Hii .map 更新优胜邻域,达到终止条件得到最终输出层。其 15)对超边进行1,次替代 中,计算邻域函数选取高斯函数,距离仍然选取欧 16)end map.cache 氏距离,WBro为SOM初始化输出层W的广播变量 17)for t+l to t do 在6)~12)中完成了一次迭代计算,旷为每次迭代 18)HBro broadcast(H) 利用每个分区样本更新后输出层,W旷:为分区合并的 19)Himp=Tky.map 输出层。 20)对样本利用H-'Bro中超边集合预测 训练集 测试集 21)end map.flatmap 22)对超边进行梯度计算 自组织神经网络 <输出层权重 23)end flatmap.reduceByKey(合并梯度值) 选择性集成 24)H'H.leftjoin(H) 训练簇1 训练簇2 训练簇c 获得s个 领域簇 25).map 26)利用合并后梯度值更新超边权重 获得s个对应 SI-MLHN SI-MLHN SI-MLHN 27)end map 局部超网络 28)end for 构成新的 超网路 29)H=H 30)return H 输出 训练过程测试过程 T为训练集经过分布式并行归一化处理后的 结果:broadcast操作可以保存只读变量,并保在每个 图2SEI-MLHN流程图 节点内存中;TBo为归一化后样本广播变量; Fig.2 Flow chart of SEI-MLHN T,Bo为样本与其k近邻的键值对T,的广播变量: 算法3S-S0M Hm为超边初始化集合;H为超边替代后集合;H 输入训练集T={(x.yn)}(1≤n≤N),类 为超边演化学习后集合。 簇个数c,学习率n,迭代次数t; 2.3 Spark下集成多标签超网络(SEI-MLHN)】 输出类簇T1,T,…,T。 SI-MLHN为MLHN的Spark平台下分布式并行 1)T =T.map 改进方法,大幅缩短了训练时间,但是其时间复杂 2)每条样本进行归一化 度仍然随着样本数量的增加呈平方级增长,仍然无 3)end map.cache 法很好适应大样本数据。故本文利用选择性集成, 4)W=初始化输出层(随机抽取c个样本) 一方面降低时间复杂度,另一方面提高算法性能, 5)WBro =broadcast(W) 提出了Spark下集成多标签超网络,记作SEL- 6)for t+1 to ti MLHN。SEI-MLHN首先将训练集进行分簇,并分别 7)for each T的分区do 用SI-MLHN算法演化学习多个局部多标签超网络。 8)for each分区内样本do 对于未知样本,首先获得近邻簇,然后利用局部超 9)利用输出层计算获胜节点 网络选择性集成对测试样本进行预测,SEI-MLHN 10)更新优胜邻域中的值为W 的流程见图2。 11)end for 为了对训练样本进行分簇,本文选择了基于神 12)end for 经网络的无监督聚类方法自组织神经网络 13)更新优胜邻域 (SOM)[。SOM对类簇初始化不敏感,并且可以 l4)W=利用reduce合并各分区W 很好地发现数据之间的结构关系,为了让其适应大 15)end for 规模数据处理将其进行了Spark下并行化扩展,记 16)T1,T,…,T。'=Tm,计算获胜节点(W) 为S-S0M。算法3为算法伪代码,首先利用每个分 17)return T,T,…,T
12)每条样本生成 e 条超边 13)end flatmap.cache 14) H 0 re = Hini .map 15)对超边进行 t r次替代 16)end map.cache 17)for t←1 to t d do 18) H t-1 re Bro = broadcast( H t-1 re ) 19)Htmp = Tkv .map 20)对样本利用 H t-1 re Bro 中超边集合预测 21)end map.flatmap 22)对超边进行梯度计算 23)end flatmap.reduceByKey(合并梯度值) 24) H t re = H t-1 re .leftjoin(Htmp ) 25).map 26)利用合并后梯度值更新超边权重 27)end map 28)end for 29)H=H t re 30)return H Tnor 为训练集经过分布式并行归一化处理后的 结果;broadcast 操作可以保存只读变量,并保在每个 节点内存中; TnorBro 为归一化后样本广播变量; TkvBro 为样本与其 k 近邻的键值对 Tkv 的广播变量; Hini为超边初始化集合; H 0 re 为超边替代后集合; H t re 为超边演化学习后集合。 2.3 Spark 下集成多标签超网络(SEI⁃MLHN) SI⁃MLHN 为 MLHN 的 Spark 平台下分布式并行 改进方法,大幅缩短了训练时间,但是其时间复杂 度仍然随着样本数量的增加呈平方级增长,仍然无 法很好适应大样本数据。 故本文利用选择性集成, 一方面降低时间复杂度,另一方面提高算法性能, 提出 了 Spark 下 集 成 多 标 签 超 网 络, 记 作 SEI⁃ MLHN。 SEI⁃MLHN 首先将训练集进行分簇,并分别 用 SI⁃MLHN 算法演化学习多个局部多标签超网络。 对于未知样本,首先获得近邻簇,然后利用局部超 网络选择性集成对测试样本进行预测,SEI⁃MLHN 的流程见图 2。 为了对训练样本进行分簇,本文选择了基于神 经网 络 的 无 监 督 聚 类 方 法 自 组 织 神 经 网 络 (SOM) [42] 。 SOM 对类簇初始化不敏感,并且可以 很好地发现数据之间的结构关系,为了让其适应大 规模数据处理将其进行了 Spark 下并行化扩展,记 为 S⁃SOM。 算法 3 为算法伪代码,首先利用每个分 区计算获胜节点,并更新优胜邻域中的输出单元, 然后将各个分区的值利用 reduce 算子进行合并,并 更新优胜邻域,达到终止条件得到最终输出层。 其 中,计算邻域函数选取高斯函数,距离仍然选取欧 氏距离, WBro 为 SOM 初始化输出层 W 的广播变量 在 6) ~12)中完成了一次迭代计算,W t c 为每次迭代 利用每个分区样本更新后输出层,W t r 为分区合并的 输出层。 图 2 SEI⁃MLHN 流程图 Fig.2 Flow chart of SEI⁃MLHN 算法 3 S⁃SOM 输入 训练集 T = {(xn ,yn )}(1 ≤ n ≤ N) ,类 簇个数 c ,学习率 η,迭代次数 t i; 输出 类簇 T1 ′,T2 ′,…,Ts ′。 1) Tnor = T .map 2)每条样本进行归一化 3)end map.cache 4) W =初始化输出层(随机抽取 c 个样本) 5) WBro = broadcast( W ) 6)for t←1 to t i 7)for each Tnor的分区 do 8)for each 分区内样本 do 9)利用输出层计算获胜节点 10)更新优胜邻域中的值为 W t c 11)end for 12)end for 13)更新优胜邻域 14)W t r =利用 reduce 合并各分区 W t c 15)end for 16)T1 ′,T2 ′,…,Tp ′ = Tnor,计算获胜节点(W t r) 17)return T1 ′,T2 ′,…,Ts ′ 第 5 期 李航,等:基于 Spark 的多标签超网络集成学习 ·629·
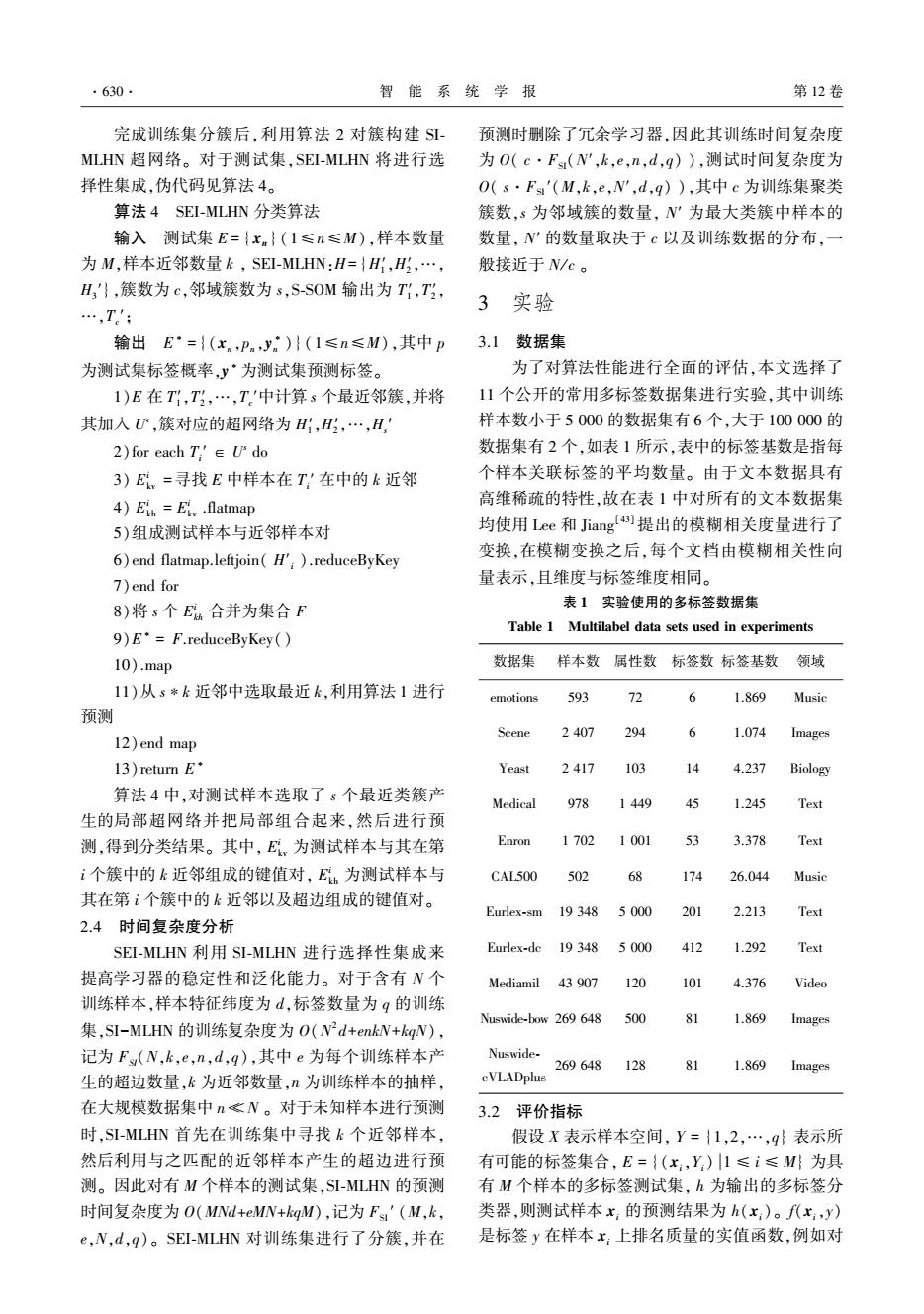
·630 智能系统学报 第12卷 完成训练集分簇后,利用算法2对簇构建S- 预测时删除了冗余学习器,因此其训练时间复杂度 MLHN超网络。对于测试集,SEI-MLHN将进行选 为O(c·Fs(N',k,e,n,d,q)),测试时间复杂度为 择性集成,伪代码见算法4。 O(s·Fs'(M,k,e,N',d,q)),其中c为训练集聚类 算法4SEI-MLHN分类算法 簇数,s为邻域簇的数量,N'为最大类簇中样本的 输入测试集E={xn}(1≤n≤M),样本数量 数量,N'的数量取决于c以及训练数据的分布,一 为M,样本近邻数量k,SEI-MLHN:H={H,H,…, 般接近于N/c。 H'},簇数为c,邻域簇数为s,S-SOM输出为T1,T, 3实验 …,T' 输出E·={(x.,Pn,y)}(1≤n≤M),其中p 3.1数据集 为测试集标签概率,y·为测试集预测标签。 为了对算法性能进行全面的评估,本文选择了 1)E在T1,T,…,T'中计算s个最近邻簇,并将 11个公开的常用多标签数据集进行实验,其中训练 其加入心,簇对应的超网络为H,H,…,H, 样本数小于5000的数据集有6个,大于100000的 2)for each T'∈Udo 数据集有2个,如表1所示,表中的标签基数是指每 3)E,=寻找E中样本在T,'在中的k近邻 个样本关联标签的平均数量。由于文本数据具有 4)Eih Eiy .flatmap 高维稀疏的特性,故在表1中对所有的文本数据集 5)组成测试样本与近邻样本对 均使用Lee和Jiang)提出的模糊相关度量进行了 6)end flatmap.leftjoin(H').reduceByKey 变换,在模糊变换之后,每个文档由模糊相关性向 7)end for 量表示,且维度与标签维度相同。 8)将s个E合并为集合F 表1实验使用的多标签数据集 Table 1 Multilabel data sets used in experiments 9)E'=F.reduceByKey() 10).map 数据集 样本数属性数标签数标签基数领域 11)从s*k近邻中选取最近k,利用算法1进行 emotions 593 12 6 1.869 Music 预测 Scene 2407 294 6 1.074 Images 12)end map l3)return E· Yeast 2417 1)3 14 4.237 Biology 算法4中,对测试样本选取了s个最近类簇产 Medical 978 1449 49 1.245 Text 生的局部超网络并把局部组合起来,然后进行预 测,得到分类结果。其中,E。为测试样本与其在第 Enron 1702 3.378 Text i个簇中的k近邻组成的键值对,E为测试样本与 CAL500 502 26.044 Music 其在第i个簇中的k近邻以及超边组成的键值对。 Eurlex-sm 19348 5000 20 2.213 Text 2.4时间复杂度分析 SEI-MLHN利用SI-MLHN进行选择性集成来 Eurlex-de 19 348 50 42 1.292 Text 提高学习器的稳定性和泛化能力。对于含有N个 Mediamil 43 907 120 101 4.376 Video 训练样本,样本特征纬度为d,标签数量为q的训练 Nuswide-bow 269 648 500 6 1.869 Images 集,SI-MLHN的训练复杂度为O(N2d+enkW+kgN), 记为F(N,k,e,n,d,g),其中e为每个训练样本产 Nuswide- 269648 128 81 1.869 Images 生的超边数量,k为近邻数量,n为训练样本的抽样, cVLADplus 在大规模数据集中n客N。对于未知样本进行预测 3.2评价指标 时,SI-MLHN首先在训练集中寻找k个近邻样本, 假设X表示样本空间,Y={1,2,…,9}表示所 然后利用与之匹配的近邻样本产生的超边进行预 有可能的标签集合,E={(x:,Y)1≤i≤M为具 测。因此对有M个样本的测试集,SI-MLHN的预测 有M个样本的多标签测试集,h为输出的多标签分 时间复杂度为O(MNd+eMN+kgM),记为Fs'(M,k, 类器,则测试样本x,的预测结果为h(x:)。f(x,y) e,N,d,q)。SEI-MLHN对训练集进行了分簇,并在 是标签y在样本x:上排名质量的实值函数,例如对
完成训练集分簇后,利用算法 2 对簇构建 SI⁃ MLHN 超网络。 对于测试集,SEI⁃MLHN 将进行选 择性集成,伪代码见算法 4。 算法 4 SEI⁃MLHN 分类算法 输入 测试集 E = { xn } (1≤n≤M),样本数量 为 M,样本近邻数量 k , SEI⁃MLHN:H= {H1 ′,H2 ′,…, H3 ′},簇数为 c,邻域簇数为 s,S⁃SOM 输出为 T1 ′,T2 ′, …,Tc ′; 输出 E ∗ = {(xn ,pn ,y ∗ n )} (1≤n≤M),其中 p 为测试集标签概率,y ∗为测试集预测标签。 1)E 在 T1 ′,T2 ′,…,Tc ′中计算 s 个最近邻簇,并将 其加入 U s ,簇对应的超网络为 H1 ′,H2 ′,…,Hs ′ 2)for each Ti ′ ∈ U s do 3) E i kv =寻找 E 中样本在 Ti ′ 在中的 k 近邻 4) E i kh = E i kv .flatmap 5)组成测试样本与近邻样本对 6)end flatmap.leftjoin( H′i ).reduceByKey 7)end for 8)将 s 个 E i kh 合并为集合 F 9)E ∗ = F.reduceByKey() 10).map 11)从 s∗k 近邻中选取最近 k,利用算法 1 进行 预测 12)end map 13)return E ∗ 算法 4 中,对测试样本选取了 s 个最近类簇产 生的局部超网络并把局部组合起来,然后进行预 测,得到分类结果。 其中, E i kv 为测试样本与其在第 i 个簇中的 k 近邻组成的键值对, E i kh 为测试样本与 其在第 i 个簇中的 k 近邻以及超边组成的键值对。 2.4 时间复杂度分析 SEI⁃MLHN 利用 SI⁃MLHN 进行选择性集成来 提高学习器的稳定性和泛化能力。 对于含有 N 个 训练样本,样本特征纬度为 d,标签数量为 q 的训练 集,SI-MLHN 的训练复杂度为 O(N 2 d+enkN+kqN), 记为 FSI(N,k,e,n,d,q),其中 e 为每个训练样本产 生的超边数量,k 为近邻数量,n 为训练样本的抽样, 在大规模数据集中 n ≪ N 。 对于未知样本进行预测 时,SI⁃MLHN 首先在训练集中寻找 k 个近邻样本, 然后利用与之匹配的近邻样本产生的超边进行预 测。 因此对有 M 个样本的测试集,SI⁃MLHN 的预测 时间复杂度为 O(MNd+eMN+kqM),记为 FSI ′ (M,k, e,N,d,q)。 SEI⁃MLHN 对训练集进行了分簇,并在 预测时删除了冗余学习器,因此其训练时间复杂度 为 O( c·FSI(N′,k,e,n,d,q) ),测试时间复杂度为 O( s·FSI ′(M,k,e,N′,d,q) ),其中 c 为训练集聚类 簇数,s 为邻域簇的数量, N′ 为最大类簇中样本的 数量, N′ 的数量取决于 c 以及训练数据的分布,一 般接近于 N/ c 。 3 实验 3.1 数据集 为了对算法性能进行全面的评估,本文选择了 11 个公开的常用多标签数据集进行实验,其中训练 样本数小于 5 000 的数据集有 6 个,大于 100 000 的 数据集有 2 个,如表 1 所示,表中的标签基数是指每 个样本关联标签的平均数量。 由于文本数据具有 高维稀疏的特性,故在表 1 中对所有的文本数据集 均使用 Lee 和 Jiang [43] 提出的模糊相关度量进行了 变换,在模糊变换之后,每个文档由模糊相关性向 量表示,且维度与标签维度相同。 表 1 实验使用的多标签数据集 Table 1 Multilabel data sets used in experiments 数据集 样本数 属性数 标签数 标签基数 领域 emotions 593 72 6 1.869 Music Scene 2 407 294 6 1.074 Images Yeast 2 417 103 14 4.237 Biology Medical 978 1 449 45 1.245 Text Enron 1 702 1 001 53 3.378 Text CAL500 502 68 174 26.044 Music Eurlex⁃sm 19 348 5 000 201 2.213 Text Eurlex⁃dc 19 348 5 000 412 1.292 Text Mediamil 43 907 120 101 4.376 Video Nuswide⁃bow 269 648 500 81 1.869 Images Nuswide⁃ cVLADplus 269 648 128 81 1.869 Images 3.2 评价指标 假设 X 表示样本空间, Y = {1,2,…,q} 表示所 有可能的标签集合, E = {(xi,Yi) 1 ≤ i ≤ M} 为具 有 M 个样本的多标签测试集, h 为输出的多标签分 类器,则测试样本 xi 的预测结果为 h(xi)。 f(xi,y) 是标签 y 在样本 xi 上排名质量的实值函数,例如对 ·630· 智 能 系 统 学 报 第 12 卷

第5期 李航,等:基于Spak的多标签超网络集成学习 .631· 于任意y1∈Y以及y2∈Y而言,f(x:,y1)>f(x, 表2实验中的比较算法 y2)成立。实值函数f代·,·)也可以转为排序函数 Table 2 Comparison of algorithms used in experiments rank(·,·),即将所有的实值输出f(x:,y)映射到 算法 参数设置 集合Y上,使得f(x:,y1)>f(xy2)时,rank(x, BRSVMI0] 基学习器:线性支持向量机 y)>rank(x,y2)也成立。基于上述描述,本文采 ML-KNN(29] smooth=1.0,近邻数=10 用的多标签性能评价指标如下。 CLRSVMI8) 基学习器:线性支持向量机 RAkEL(9] 标签集k=3,集成大小=2g 1)Hamming Loss:用于考察样本在单个标签上 基学习器:线性支持向量机 的误分类情况。 ECCt23] 集成大小=50 hloss(h)= Ih(x)△Y M台Q IBLR44] 近邻数=10 式中△表示两个集合的对称差。 COCOAL4] k=10 S-CoMLHN(24) 近邻数=20,7=0.01 2)One-eror:用于考察样本测标签排序集合中 SI-MLHN 近邻数=10,7=0.01 最前端的标签误分类的情况。 表3实验单节点环境 one-error (f)= [(arg maxf(,y))y] Table 3 Experimental environment 3)Ranking Loss:用于考察样本的预测标签排序 处理器单CPU CPU频率/CPU内存容量/是否支持 集合中的错排情况。 型号 核心数 GHz 个数 GB 超线程 E5-2620 6 2.0 2 64 是 rloss,(f)= 表4集群环境配置 Table 4 Configuration in clustered environment L=(y12)lfx出)≤fxy2),(y1y2)eY:×Y 式中Y是Y,的补集。 集群配置 版本号 4)Average Precision:用于考察样本的预测标签 操作系统 Cent OS6.5 集合中排在该样本标签之前的标签分类正确的 节点个数 16 情况。 1 1 Scala版本 2.10.4 avgpre,=7Y' Hadoop版本 2.5.2 |{y'rank(x:y')≤rank(x:,y),y'eY}l Spark版本 1.5.1 rank(x;,y) 5)Example Based F: JDK版本 1.7 1兴2|y:nh(x) 3.4实验结果 F,=M名Y+h(刀 3.4.1参数分析 3.3比较的算法和实验环境 对于算法SEI-MLHN,近邻个数k是关键参数 在本文中,将SEI-MLHN与两种系列的算法进 之一,为了测试算法对k参数的敏感度,本节将k以 行比较实验,第1种系列是常用的多标签学习算法, 5为步长,在5~40范围内测试算法SI-MLHN的性 如表2的前8种算法所示,它们均在表3所示的单 能。如图3所示,(c)、(e)随k的增大波动较大,部 节点环境中实现。第二种系列是在Spak平台下实 分数据集k>10后趋于稳定,多数数据集随k增大性 现的超网络多标签学习算法,如S-CoMLHN以及 能变差;(a)中对k值不敏感,几乎没有变化:(b)随 SEL-MLHN的基学习器SI-MLHN,Spark集群环境如 k值增大性能变好,且在k>10后趋于平稳:在(d) 表4所示,其中S-CoMLHN是Co-MLHN在Spark平 中不同的数据集随着k值的变化,性能既有增加的, 台下的实现。 也有降低的,但总体上在k=10时,能有较好的性 在实验过程中比较算法的参数设置取自文献 [8-9,14,24,30,39,44],详细设置见表3,其中算法 能。这是由于k值直接关系着预测样本的匹配超边 Sl-MLHN中每个样本生成超边的数量e为10,超边 数量,当k太小时与之匹配的超边数量太小,会漏掉 替代迭代次数t,为5,随机梯度下降迭代次数t 一些相关标签,k值太大则会引入噪声标签且会影 为5。 响算法运行效率,故本文将k取为10
于任意 y1 ∈ Y 以及 y2 ∈ Y 而言, f(xi,y1 ) > f(xi, y2 ) 成立。 实值函数 f(·,·) 也可以转为排序函数 rankf(·,·) ,即将所有的实值输出 f(xi,y) 映射到 集合 Y 上,使得 f(xi,y1 ) > f(xi,y2 ) 时, rankf(xi, y1 ) > rankf(xi,y2 ) 也成立。 基于上述描述,本文采 用的多标签性能评价指标如下。 1)Hamming Loss: 用于考察样本在单个标签上 的误分类情况。 hloss(h) = 1 M∑ M i = 1 1 Q h(xi)ΔYi 式中 Δ 表示两个集合的对称差。 2)One⁃error:用于考察样本测标签排序集合中 最前端的标签误分类的情况。 one⁃errors(f) = 1 M∑ M i = 1 [ arg max y∈Y f(xi,y) ) ∉ Yi ( ] 3)Ranking Loss:用于考察样本的预测标签排序 集合中的错排情况。 rlosss(f) = 1 M∑ M i = 1 L Yi Yi L = (y1,y2) f(xi,y1) ≤ f(xi,y2),(y1,y2) ∈ Yi × Yi 式中 Yi 是 Yi 的补集。 4)Average Precision:用于考察样本的预测标签 集合中排在该样本标签之前的标签分类正确的 情况。 avgprecs(f) = 1 M∑ M i = 1 1 Yi · ∑y∈Yi {y′ rankf(xi,y′) ≤ rankf(xi,y),y′ ∈ Yi} rankf(xi,y) 5) Example Based F1 : F1 = 1 M∑ M i = 1 2 Yi ∩ h(xi) Yi + h(xi) 3.3 比较的算法和实验环境 在本文中,将 SEI⁃MLHN 与两种系列的算法进 行比较实验,第 1 种系列是常用的多标签学习算法, 如表 2 的前 8 种算法所示,它们均在表 3 所示的单 节点环境中实现。 第二种系列是在 Spark 平台下实 现的超网络多标签学习算法,如 S⁃CoMLHN 以及 SEI⁃MLHN 的基学习器 SI⁃MLHN,Spark 集群环境如 表 4 所示,其中 S⁃CoMLHN 是 Co⁃MLHN 在 Spark 平 台下的实现。 在实验过程中比较算法的参数设置取自文献 [8-9,14,24,30,39,44],详细设置见表 3,其中算法 SI⁃MLHN 中每个样本生成超边的数量 e 为 10,超边 替代迭代次数 t r 为 5,随机梯度下降迭代次数 t d 为 5。 表 2 实验中的比较算法 Table 2 Comparison of algorithms used in experiments 算法 参数设置 BRSVM [30] 基学习器:线性支持向量机 ML⁃KNN [29] smooth = 1.0, 近邻数= 10 CLRSVM [8] 基学习器:线性支持向量机 RAkEL [9] 标签集 k = 3, 集成大小= 2q ECC [33] 基学习器:线性支持向量机 集成大小= 50 IBLR [44] 近邻数= 10 COCOA [14] k = 10 S⁃CoMLHN [24] 近邻数= 20,η = 0.01 SI⁃MLHN 近邻数= 10, η = 0.01 表 3 实验单节点环境 Table 3 Experimental environment 处理器 型号 单 CPU 核心数 CPU 频率/ GHz CPU 个数 内存容量/ GB 是否支持 超线程 E5⁃2620 6 2.0 2 64 是 表 4 集群环境配置 Table 4 Configuration in clustered environment 集群配置 版本号 操作系统 Cent OS6.5 节点个数 16 Scala 版本 2.10.4 Hadoop 版本 2.5.2 Spark 版本 1.5.1 JDK 版本 1.7 3.4 实验结果 3.4.1 参数分析 对于算法 SEI⁃MLHN,近邻个数 k 是关键参数 之一,为了测试算法对 k 参数的敏感度,本节将 k 以 5 为步长,在 5 ~ 40 范围内测试算法 SI⁃MLHN 的性 能。 如图 3 所示,(c)、(e)随 k 的增大波动较大,部 分数据集 k>10 后趋于稳定,多数数据集随 k 增大性 能变差;(a)中对 k 值不敏感,几乎没有变化;(b)随 k 值增大性能变好,且在 k > 10 后趋于平稳;在(d) 中不同的数据集随着 k 值的变化,性能既有增加的, 也有降低的,但总体上在 k = 10 时,能有较好的性 能。 这是由于 k 值直接关系着预测样本的匹配超边 数量,当 k 太小时与之匹配的超边数量太小,会漏掉 一些相关标签,k 值太大则会引入噪声标签且会影 响算法运行效率,故本文将 k 取为 10。 第 5 期 李航,等:基于 Spark 的多标签超网络集成学习 ·631·
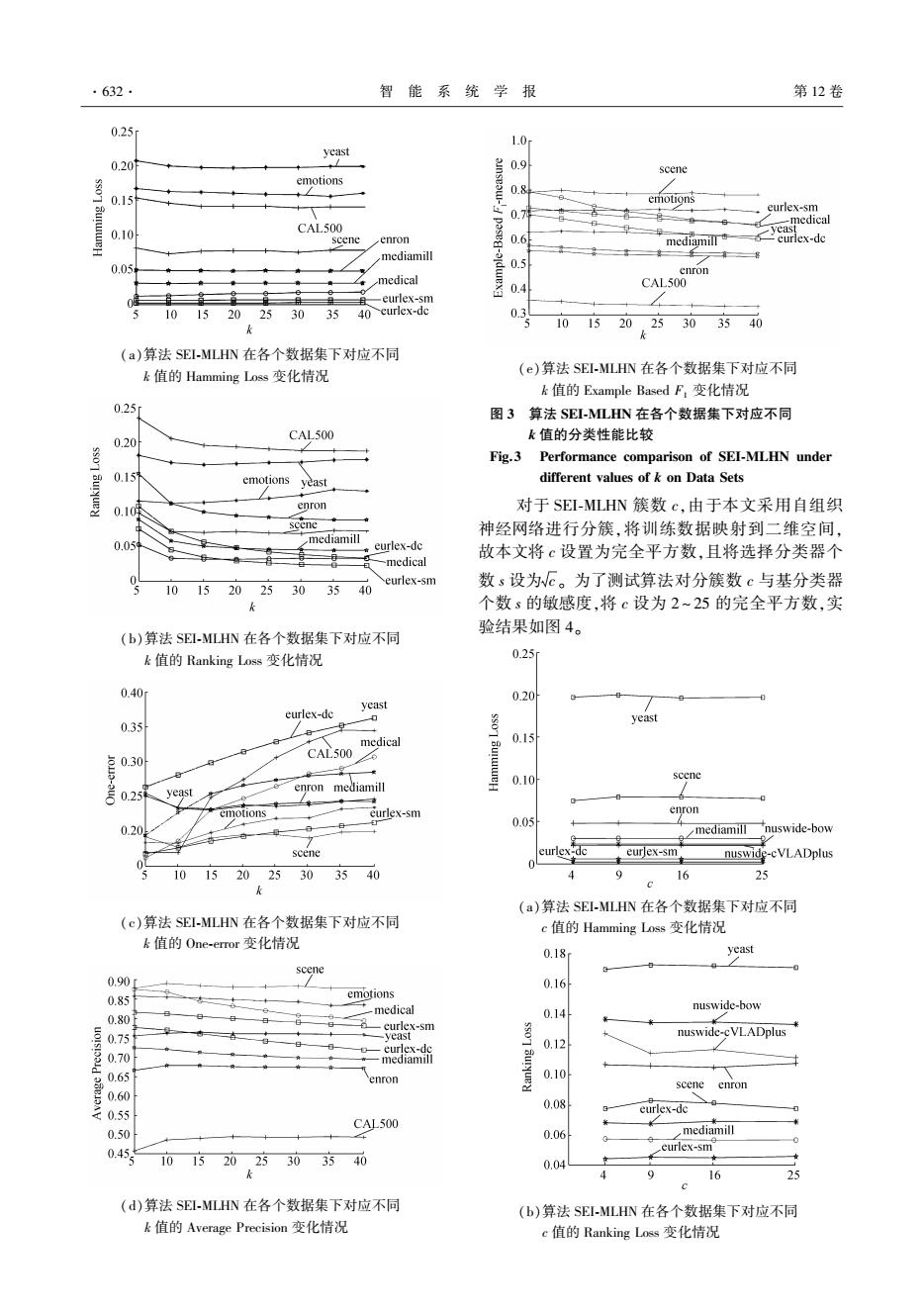
·632. 智能系统学报 第12卷 0.25 1.0 yeast 0.20 scene emotions 0.8 0.15 emotions 0.74 eurlex-sm CAL500 -medical 0.10 scene enron 0.6 mediamill Ycuex-dc mediamill 0.05 ron medical 0.4 CAL500 eurlex-sm 1015202530 35 40 curlex-de 0.3 10152025 303540 (a)算法SEI-MLHN在各个数据集下对应不同 k值的Hamming Loss变化情况 (e)算法SEI-MLHN在各个数据集下对应不同 k值的Example Based F,变化情况 0.25 图3算法SEI-MLHN在各个数据集下对应不同 CAL500 0.20 k值的分类性能比较 Fig.3 Performance comparison of SEI-MLHN under 0.151 emotions yeast different values of k on Data Sets 0.10 enron 对于SEI-MLHN簇数c,由于本文采用自组织 scene 神经网络进行分簇,将训练数据映射到二维空间, 0.05 mediamill eurlex-dc 故本文将c设置为完全平方数,且将选择分类器个 medical eurlex-sm 数s设为C。为了测试算法对分簇数c与基分类器 1015 2025 30 35 40 个数s的敏感度,将c设为2~25的完全平方数,实 验结果如图4。 (b)算法SEI-MLHN在各个数据集下对应不同 k值的Ranking Loss变化情况 0.25 0.40 0.20 yeast eurlex-dc yeast 0.35 medical 0.15 CAL500 50.30 yeast enron mediamill 0.10 emotions eurlex-sm enron 0.05 0.20 mediamill nuswide-bow scene eurlex-dc eurlex-sm 0 nuswide-cVLADplus 10 152025 303540 9 6 25 (a)算法SEI-MLHN在各个数据集下对应不同 (c)算法SEI-MLHN在各个数据集下对应不同 c值的Hamming Loss变化情况 k值的One-emor变化情况 0.18m yeast scene G 0.90 0.16 0.85 emotions medical 0.14 nuswide-bow 0.80 0.75 erex-sm nuswide-cVLADplus eurl 0.12 0.70 065 enron 0.10 scene enron 0.60 0.08 0.55 eurlex-dc CAL500 米 0.50 0.06 mediamill 0.455 eurlex-sm 10152025303540 0.04 4 9 16 25 c (d)算法SEI-MLHN在各个数据集下对应不同 (b)算法SEI-MLHN在各个数据集下对应不同 k值的Average Precision变化情况 c值的Ranking Loss变化情况
(a)算法 SEI⁃MLHN 在各个数据集下对应不同 k 值的 Hamming Loss 变化情况 (b)算法 SEI⁃MLHN 在各个数据集下对应不同 k 值的 Ranking Loss 变化情况 (c)算法 SEI⁃MLHN 在各个数据集下对应不同 k 值的 One⁃error 变化情况 (d)算法 SEI⁃MLHN 在各个数据集下对应不同 k 值的 Average Precision 变化情况 (e)算法 SEI⁃MLHN 在各个数据集下对应不同 k 值的 Example Based F1 变化情况 图 3 算法 SEI⁃MLHN 在各个数据集下对应不同 k 值的分类性能比较 Fig.3 Performance comparison of SEI⁃MLHN under different values of k on Data Sets 对于 SEI⁃MLHN 簇数 c,由于本文采用自组织 神经网络进行分簇,将训练数据映射到二维空间, 故本文将 c 设置为完全平方数,且将选择分类器个 数 s 设为 c 。 为了测试算法对分簇数 c 与基分类器 个数 s 的敏感度,将 c 设为 2 ~ 25 的完全平方数,实 验结果如图 4。 (a)算法 SEI⁃MLHN 在各个数据集下对应不同 c 值的 Hamming Loss 变化情况 (b)算法 SEI⁃MLHN 在各个数据集下对应不同 c 值的 Ranking Loss 变化情况 ·632· 智 能 系 统 学 报 第 12 卷

第5期 李航,等:基于Spak的多标签超网络集成学习 ·633. 0.45 图4中,(a)、(c)、(d)、(e)中算法SEI-MLHN nuswide-bow 0.40 在各个数据集中的性能几乎不变或变化幅度非常 0.35 nuswide-cVLADplus 小,说明Hamming Loss、One-eror、Average Precision 和Example Based F,对c和s的变化不敏感,(b)中 0.30 eurlex-dc SEI-MLHN的性能在数据集nuswide-cVLADplus中 0.25 enron 随c和s的增大有小幅度的优化,()中可以看出较 0.20 mediamill yeast scene 小规模数据随簇数c和s的增加训练时间小幅增 0.15 eurlex-sm 加,而对于大规模数据集,算法训练时间大幅减少。 16 25 (c)算法SEI-MLHN在各个数据集下对应不同 故本文对样本数量小于10000的训练集,c和s分 c值的One-emor变化情况 别选取4和2:样本数量在10000到100000之间的 0.90r 0.85 scene eurlex-sm 训练集,c和s分别选取9和3;样本数量大于 ★ 0.80 eurlex-dc 100000的训练集,c和s分别选取25和5。 0.75 ediami专 0 yeast 0 3.4.2分类性能比较 在实验中,所有的多标签学习算法均采用相同 左0.65 enron 的数据划分,用50%的数据进行训练,其余50%的 0.60 nuswide-cVLADplus 数据进行测试。在计算评价指标时,评价指标取重 0.50 nuswide-bow 复10次实验的平均值。由于比较的部分算法无法 0.45 在一周内对数据集nuswide-.cVLADplus、nuswide-bow (d)算法SEI-MHN在各个数据集下对应不同 c值的Average Precision变化情况 完成训练预测,故在对算法性能进行比较与分析时 0.80 G 8 只取其余9个数据集进行实验,如表5所示。在表 0.75 scene eurlex-sm 6中列出了本文算法在nuswide-.bow、nuswide- 0.70 0.65 eurlex-dc cVLADplus数据集上的评价指标值。 0.60 yeast mediamill 表5为5个不同评价指标下各个多标签学习算 0.55 enron 法在常规规模的数据集上的学习性能,表5中评价 0.50 0.45 指标后的“↓”表示指标取值越小性能越佳,符号 0.40 nuswide-cVLADplus “↑”表示指标取值越大性能越佳,其中AveR表示 0.35 十 + nuswide-bow 0.30 该算法的平均排名。此外,表7对每个学习算法进 16 (e)算法SEI-MLHN在各个数据集下对应不同 行编号,例如BRSVM(A,)表示用A,代表算法 c值的Example Based F,变化情况 BRSVM,再进一步给出了各多标签学习算法之间的 4.5r×10 4.0 相对性能,具体为,给定算法A1和A2,A,>A2表示在 3.5 nuswide-cVLADplus 给定的评价指标上,基于显著度0.05的威尔科克森 3.0 符号秩检验(Wilcoxon signed rank test),算法A,的 2.5 性能显著优于A2。本文通过打分的方式对各学习 2.0 1.5 nuswide-bow 算法的性能进行总体评价,若A,>A2,则A,的分数 1.0 加1,A2的分数减1,通过比较每个算法的最终分 0.5 scene mediamill eurlex-dc 数,可以对算法进行排序,其中A,分数高于A2,表 0enron 4 9 言a-sm 16 示算法A,的总体性能优于A2。 (f)算法SEI-MLHN在各个数据集下对应不同 从表7中可以发现,算法SEI-MLHN在除 c值的Train time变化情况 图4算法SEI-MLHN在各个数据集下对应不同c值 Ranking loss外的各项指标以及总分均显著高于其 的分类性能比较 余算法,表明它的分类性能在总体上优于其余算 Fig.4 Performance comparison of SEI-MLHN under different values of c on Data Sets 法。其次,算法SL-MLHN在Example based F,上明
(c)算法 SEI⁃MLHN 在各个数据集下对应不同 c 值的 One⁃error 变化情况 (d)算法 SEI⁃MLHN 在各个数据集下对应不同 c 值的 Average Precision 变化情况 (e)算法 SEI⁃MLHN 在各个数据集下对应不同 c 值的 Example Based F1 变化情况 (f)算法 SEI⁃MLHN 在各个数据集下对应不同 c 值的 Train time 变化情况 图 4 算法 SEI⁃MLHN 在各个数据集下对应不同 c 值 的分类性能比较 Fig.4 Performance comparison of SEI⁃MLHN under different values of c on Data Sets 图 4 中,(a)、(c)、(d)、(e)中算法 SEI⁃MLHN 在各个数据集中的性能几乎不变或变化幅度非常 小,说明 Hamming Loss 、One⁃error、Average Precision 和 Example Based F1对 c 和 s 的变化不敏感,(b)中 SEI⁃MLHN 的性能在数据集 nuswide⁃cVLADplus 中 随 c 和 s 的增大有小幅度的优化,(f)中可以看出较 小规模数据随簇数 c 和 s 的增加训练时间小幅增 加,而对于大规模数据集,算法训练时间大幅减少。 故本文对样本数量小于 10 000 的训练集,c 和 s 分 别选取 4 和 2;样本数量在 10 000 到 100 000 之间的 训练集, c 和 s 分别选 取 9 和 3; 样 本 数 量 大 于 100 000的训练集,c 和 s 分别选取 25 和 5。 3.4.2 分类性能比较 在实验中,所有的多标签学习算法均采用相同 的数据划分,用 50%的数据进行训练,其余 50%的 数据进行测试。 在计算评价指标时,评价指标取重 复 10 次实验的平均值。 由于比较的部分算法无法 在一周内对数据集 nuswide⁃cVLADplus、nuswide⁃bow 完成训练预测,故在对算法性能进行比较与分析时 只取其余 9 个数据集进行实验,如表 5 所示。 在表 6 中 列 出 了 本 文 算 法 在 nuswide⁃bow、 nuswide⁃ cVLADplus 数据集上的评价指标值。 表 5 为 5 个不同评价指标下各个多标签学习算 法在常规规模的数据集上的学习性能,表 5 中评价 指标后的“↓” 表示指标取值越小性能越佳,符号 “↑”表示指标取值越大性能越佳,其中 AveR 表示 该算法的平均排名。 此外,表 7 对每个学习算法进 行编号, 例 如 BRSVM ( A1 ) 表 示 用 A1 代 表 算 法 BRSVM,再进一步给出了各多标签学习算法之间的 相对性能,具体为,给定算法 A1 和 A2 ,A1>A2 表示在 给定的评价指标上,基于显著度 0.05 的威尔科克森 符号秩检验(Wilcoxon signed rank test),算法 A1 的 性能显著优于 A2 。 本文通过打分的方式对各学习 算法的性能进行总体评价,若 A1 > A2 ,则 A1 的分数 加 1,A2 的分数减 1,通过比较每个算法的最终分 数,可以对算法进行排序,其中 A1 分数高于 A2 ,表 示算法 A1 的总体性能优于 A2 。 从表 7 中 可 以 发 现, 算 法 SEI⁃MLHN 在 除 Ranking loss 外的各项指标以及总分均显著高于其 余算法,表明它的分类性能在总体上优于其余算 法。 其次, 算法 SI⁃MLHN 在 Example based F1 上明 第 5 期 李航,等:基于 Spark 的多标签超网络集成学习 ·633·