
第五章热力学第二定律调 The second law of thermodynamics 5-1热力学第二定律 5-2卡诺循环和卡诺定理 5-3熵和热力学第二定律的数学表达式 5-4熵方程与孤立系统熵增原理 5-5系统的作功能力(火用)及熵产与作功能力损失 5-6火用平衡方程及火用损失 密
1 第五章 热力学第二定律 The second law of thermodynamics 5-1 热力学第二定律 5-2 卡诺循环和卡诺定理 5–3 熵和热力学第二定律的数学表达式 5–4 熵方程与孤立系统熵增原理 5-5 系统的作功能力(火用)及熵产与作功能力损失 5-6 火用平衡方程及火用损失
5-1热力学第二定律 自发过程的方向性 高 只要Q不大于Q,并不违反第一定律 2
2 5–1 热力学第二定律 一、自发过程的方向性 只要Q'不大于Q,并不违反第一定律 Q Q' ?
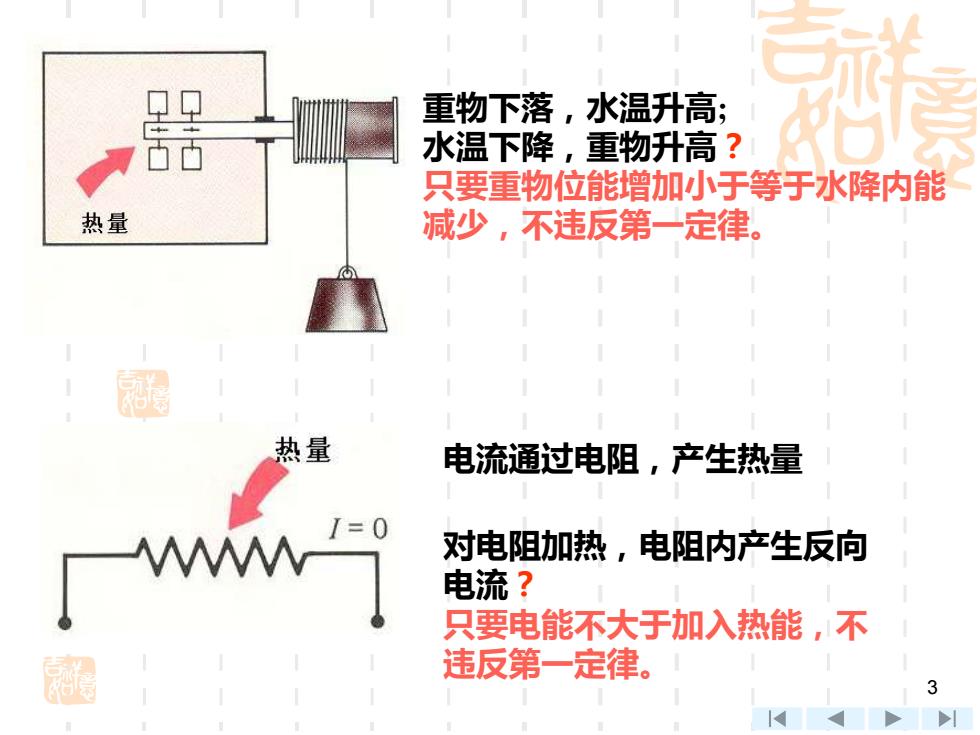
重物下落,水温升高; 水温下降,重物升高? 只要重物位能增加小于等于水降内能 热量 减少,不违反第一定律。 热量 电流通过电阻,产生热量 7=0 对电阻加热,电阻内产生反向 电流? 只要电能不大于加入热能,不 违反第一定律。 3
3 重物下落,水温升高; 水温下降,重物升高? 只要重物位能增加小于等于水降内能 减少,不违反第一定律。 电流通过电阻,产生热量 对电阻加热,电阻内产生反向 电流? 只要电能不大于加入热能,不 违反第一定律

归纳:1)自发过程有方向性; 2)自发过程的反方向过程并非不可进行,而是 要有附加条件; 3)并非所有不违反第一定律的过程均可进行。 无限可转换能一机械能,电能 能量转换方向性的 部分可转换能一热能 实质是能质有差异 T≠T 圈 不可转换能一环境介质的热力学能
4 归纳:1)自发过程有方向性; 2)自发过程的反方向过程并非不可进行,而是 要有附加条件; 3)并非所有不违反第一定律的过程均可进行。 能量转换方向性的 实质是能质有差异 无限可转换能—机械能,电能 部分可转换能—热能 T T0 不可转换能—环境介质的热力学能
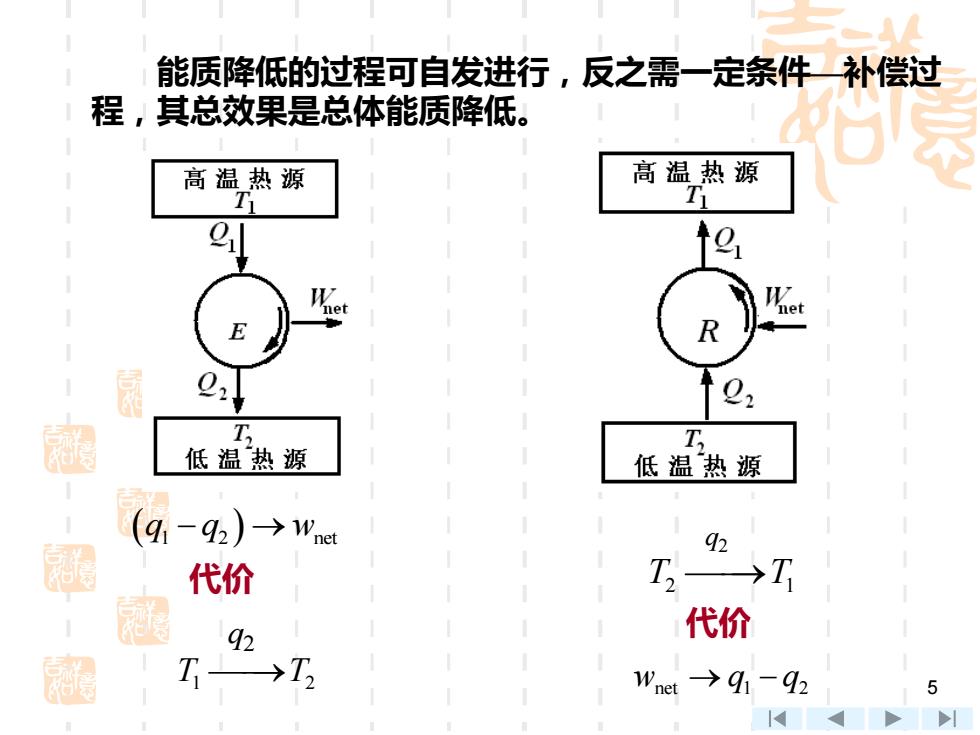
能质降低的过程可自发进行,反之需一定条件补偿过 程,其总效果是总体能质降低。 高温热源 高温热源 et Q, 2, T T 低温热源 低温热源 (9 1-92)-→1"net 92 代价 →T 92 代价 T→T Wnet →91-92 5
5 能质降低的过程可自发进行,反之需一定条件—补偿过 程,其总效果是总体能质降低。 (q q w 1 2 net − →) 代价 T T 1 2 ⎯⎯→2 q T T 2 1 ⎯⎯→2 q w q q net 1 2 → − 代价
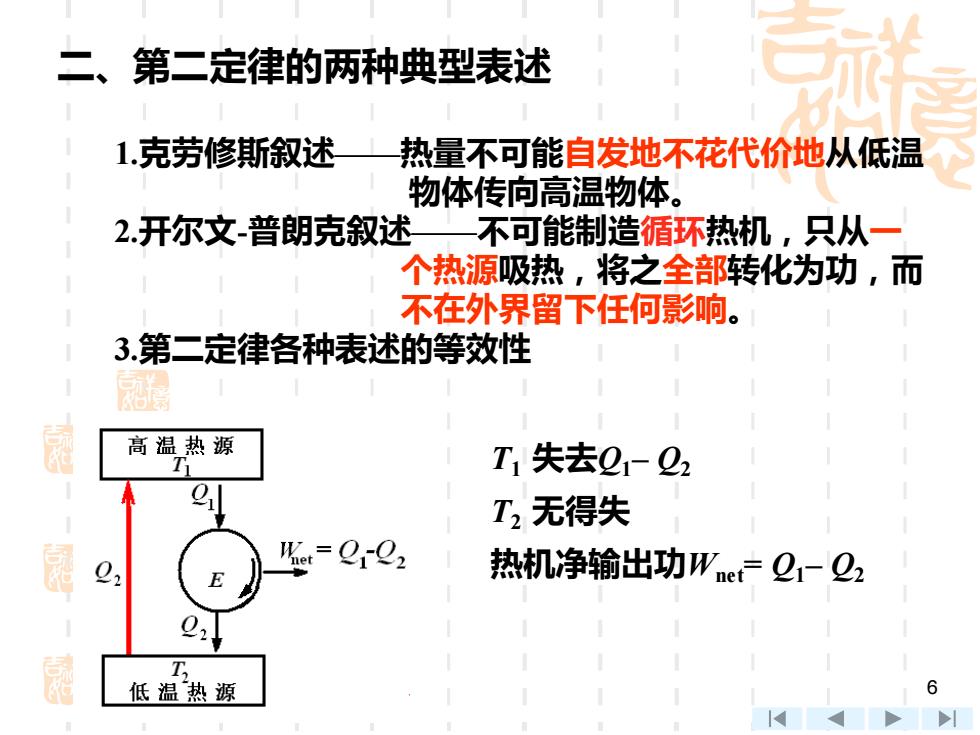
二、第二定律的两种典型表述 1.克劳修斯叙述 热量不可能自发地不花代价地从低温 物体传向高温物体。 2开尔文-普朗克叙述—不可能制造循环热机,只从一 个热源吸热,将之全部转化为功,而 不在外界留下任何影响。 3第二定律各种表述的等效性 和 高温热源 T1失去21-22 T2无得失 02 2r2: 热机净输出功Wne=1-22 0 屋 低温热源 6
6 二、第二定律的两种典型表述 1.克劳修斯叙述——热量不可能自发地不花代价地从低温 物体传向高温物体。 2.开尔文-普朗克叙述——不可能制造循环热机,只从一 个热源吸热,将之全部转化为功,而 不在外界留下任何影响。 3.第二定律各种表述的等效性 T1 失去Q1– Q2 T2 无得失 热机净输出功Wnet= Q1– Q2
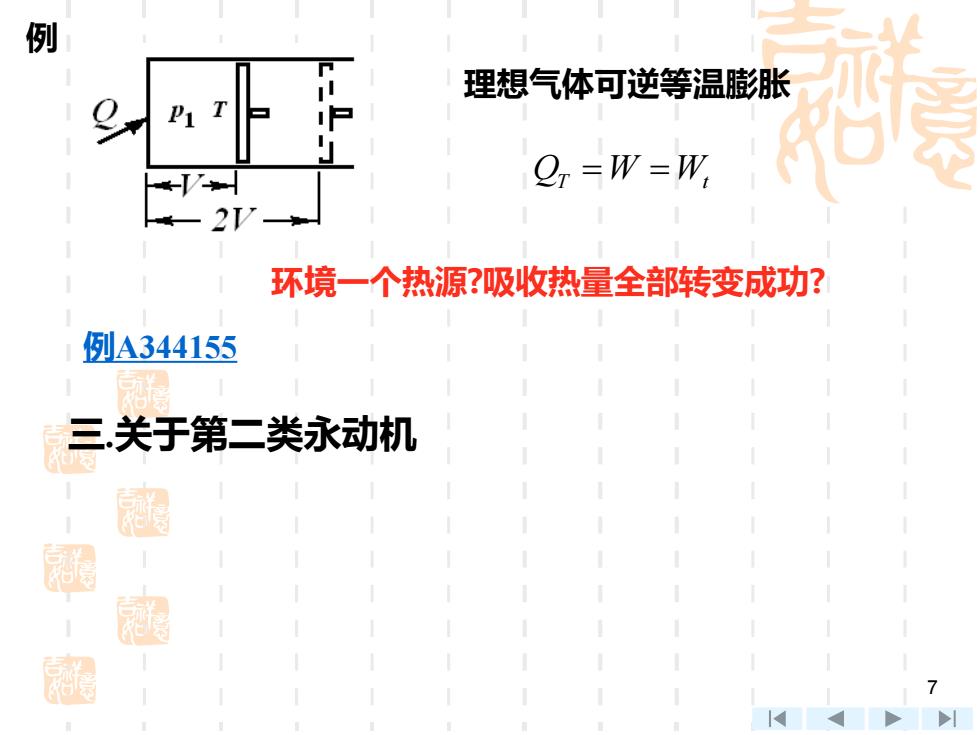
例 理想气体可逆等温膨胀 P1 O.-W-W. 环境一个热源?吸收热量全部转变成功? 例A344155 三关于第二类永动机 周 虚 超
7 三.关于第二类永动机 理想气体可逆等温膨胀 Q W W T t = = 环境一个热源?吸收热量全部转变成功? 例 例A344155
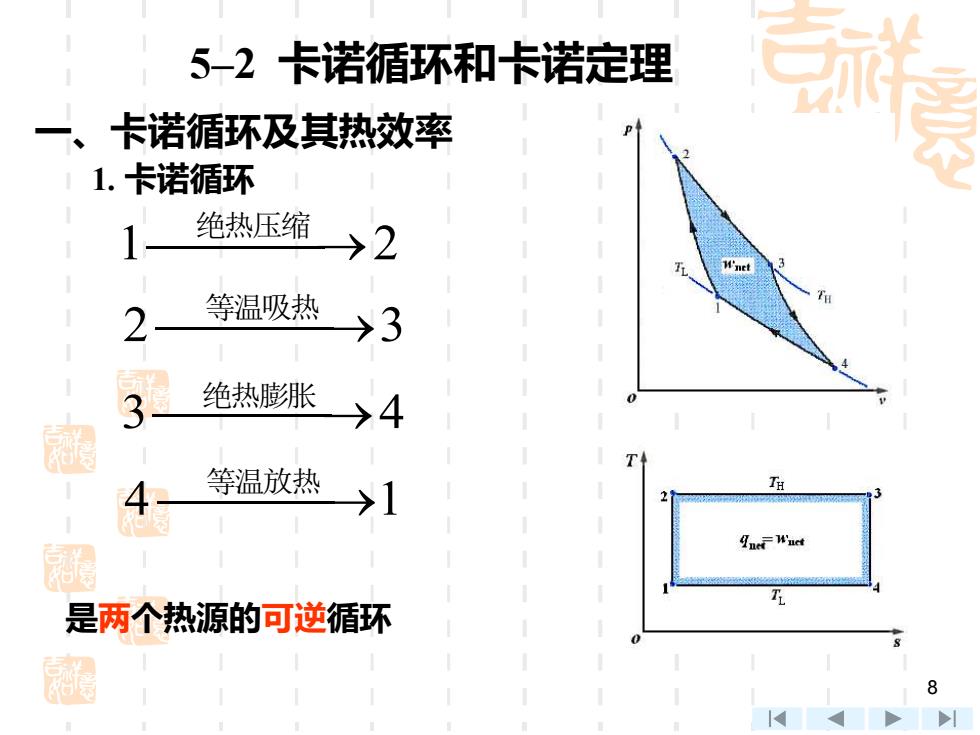
5-2卡诺循环和卡诺定理 卡诺循环及其热效率 1.卡诺循环 绝热压缩 →2 2 等温吸热 >3 3 绝热膨胀 >4 等温放热 >1 SneWuct 墨 是两个热源的可逆循环 超 8 >l
8 5–2 卡诺循环和卡诺定理 一、卡诺循环及其热效率 1. 卡诺循环 1⎯⎯ ⎯→2 绝热压缩 是两个热源的可逆循环 2 ⎯⎯ ⎯→3 等温吸热 3⎯⎯ ⎯→4 绝热膨胀 4 ⎯⎯ ⎯→1 等温放热
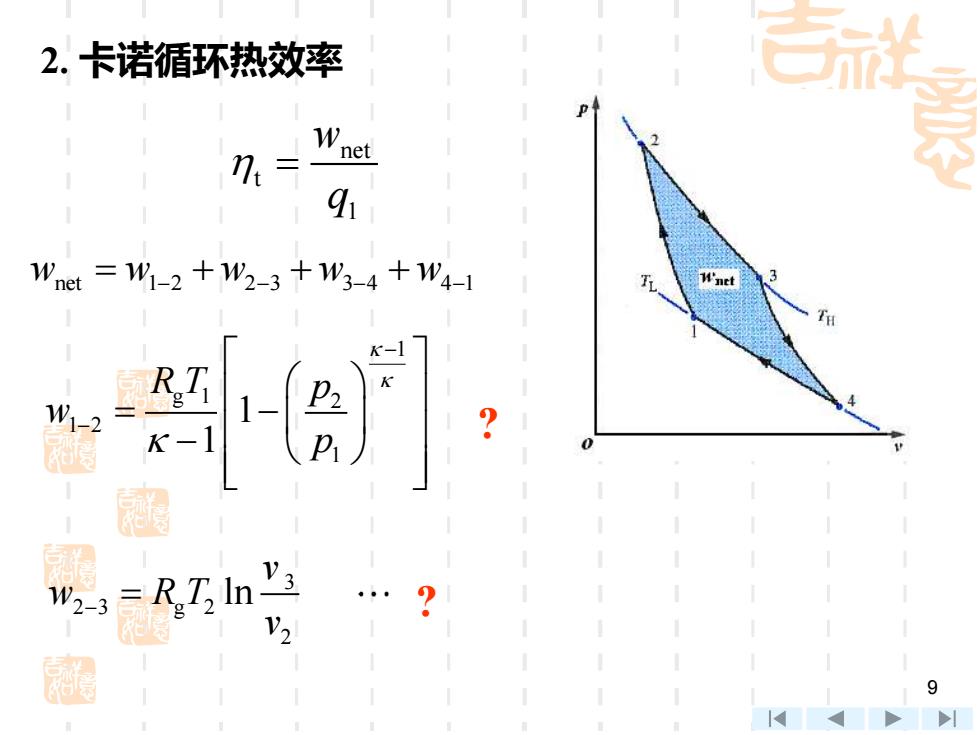
2.卡诺循环热效率 W 7:= net 91 Wnet=W1-2十%2-3十W3-4+w4-1 W'ntt W1-2 RT In V2
9 2. 卡诺循环热效率 net t 1 w q = w w w w w net 1 2 2 3 3 4 4 1 = + + + − − − − 1 g 1 2 1 2 1 1 1 R T p w p − − = − − ? ? 3 2 3 g 2 2 ln v w R T v − =

-4 9(=9放)=941=T(S-S4) g=(=9®)=93=7(s,-$) 9net=91-92 =(TH-Ti)AS23=Wnct 2-1分 THAS23 10
10 q q q T s s 2 4 1 L 1 4 (= = = − 放 ) − ( ) ( H L 23 ) L c H 23 H 1 T T s T T s T − = = − q q q T s s 1 2 3 H 3 2 = = = = − ( 吸 ) − ( ) net 1 2 q q q = − = − = (T T s w H L 23 net )