《工程热力学》课程教学资源（PPT课件）第二章 热力学第一定律 First law of thermodynamics

第二章热力学第一定律 First law of thermodynamics 2-1热力学第一定律的实质 2-2热力学能（内能）和总能 2-3热力学第一定律基本表达式 超 2-4闭口系基本能量方程式 周 2-5开口系能量方程 超

1 第二章 热力学第一定律 First law of thermodynamics 2–1 热力学第一定律的实质 2-2 热力学能（内能）和总能 2–3 热力学第一定律基本表达式 2–4 闭口系基本能量方程式 2–5 开口系能量方程

2-1热力学第一定律的实质 一、第一定律的实质 能量守恒与转换定律在热现象中的应用。 二、第一定律的表述 热是能的一种，机械能变热能，或热能变机械能的 时候，他们之间的比值是一定的。 或： 热可以变为功，功也可以变为热；一定量的热消失 时必定产生相应量的功；消耗一定量的功时，必出现 与之相应量的热。 和

2 2–1 热力学第一定律的实质 一、第一定律的实质 能量守恒与转换定律在热现象中的应用。 二、第一定律的表述 热是能的一种，机械能变热能，或热能变机械能的 时候，他们之间的比值是一定的。 或： 热可以变为功，功也可以变为热；一定量的热消失 时必定产生相应量的功；消耗一定量的功时，必出现 与之相应量的热

2-2热力学能（内能)和总能 一、 热力学能(internal energy) Uch 平移动能 转动动能 振动动能 U。-f2(T,v) r-a 二、总（储存）能(total stored energy of system) 热力学能，内部储存能 圈 E-U4R+E e-utg te 宏观动能 宏观位能 总能 外部储存能

3 2–2 热力学能（内能）和总能 一、热力学能(internal energy) U Uch Unu Uth Uk 平移动能 转动动能 振动动能 f T  1 Up— f T , v 2 U  U(T,v) 二、总（储存）能(total stored energy of system) E U Ek Ep k p    eue e 总能 热力学能，内部储存能 外部储存能 宏观动能 宏观位能

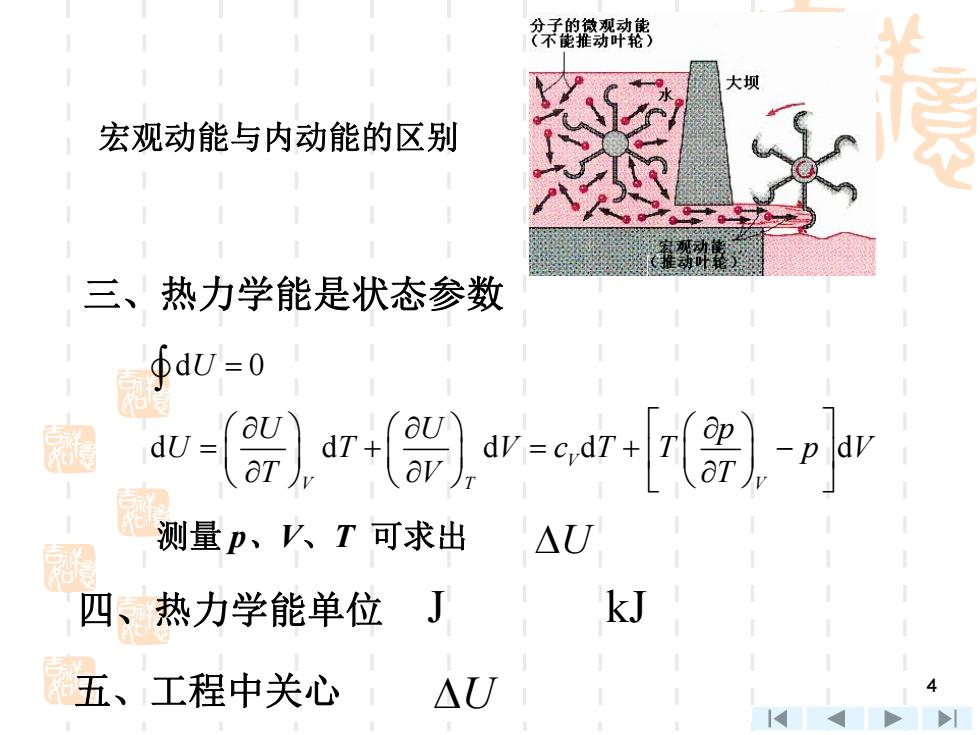
柔餐醉转 宏观动能与内动能的区别 三、热力学能是状态参数 ∮dU=0 du= )d+)d业-cd+7器-p 测量p、V、T可求出 △J 四、热力学能单位J kJ 五、工程中关心 △U

4 三、热力学能是状态参数 测量 p、V、T 可求出 d 0 d d d d d V V T V U U U p U T V c T T p V T V T                                      U 四、热力学能单位 J kJ 五、工程中关心 U 宏观动能与内动能的区别

2-3热力学第一定律基本表达式 加入系统的能量总和一热力系统输出的能量总和 =热力系总储存能的增量 δW δm,ei δm,ej E+dE δ9 7+d 流入：δ2+∑òm,e 流出：δW+∑òm,e 内部贮能的增量：dE 圈

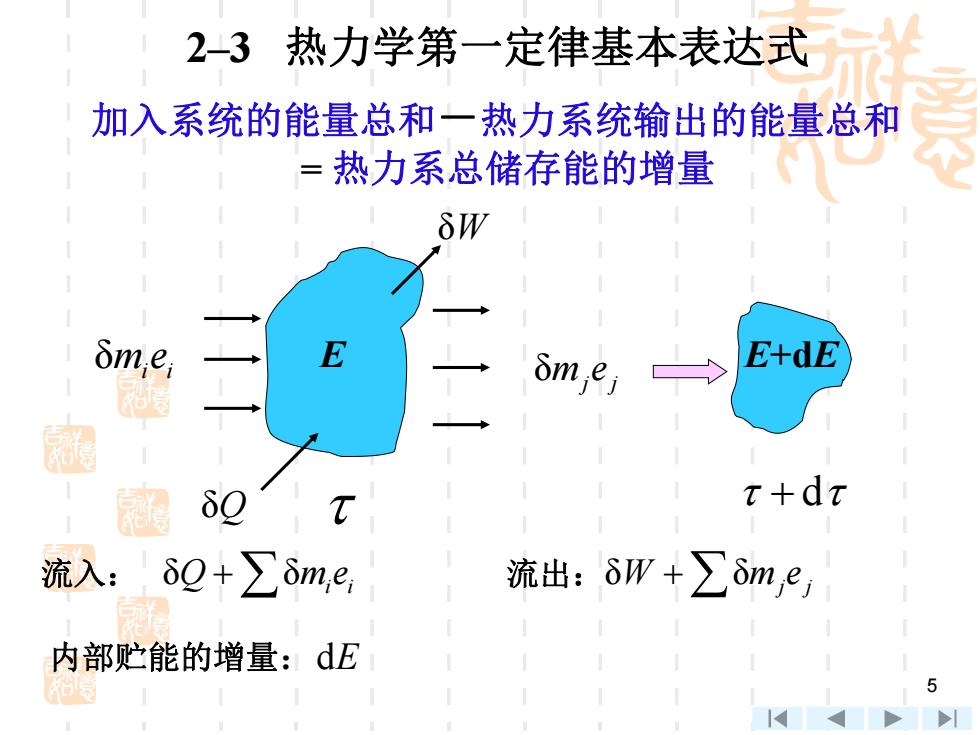
5 2–3 热力学第一定律基本表达式 加入系统的能量总和－热力系统输出的能量总和 = 热力系总储存能的增量 δmiei E E+dE δQ δW δmj j e   d  流入： δ δ Q mi i  e 流出：δ δ W mj j  e 内部贮能的增量：dE

δ δm,ei δm,ej E+dE δQ 起 δ0=dE+[z(e,im）-(emr)】+δm。 或 度e=A&+[em,）-(emr)】]+m Φ= 是 +[eaa)(egw】+ra 6

6     tot δ d δ δ δ Q E j j i i   e m  e m  W   或     2 1 tot δ δ Q E j j i i e m e m W               tot d d j mj i mi E e q eq P        δmiei E E+dE δQ δW δmj j e    d

2-4闭口系基本能量方程式 p=E+[ze,m）-z(em)】]+项。 闭口系， δm=0 8n,=0 忽略宏观动能U和位能Up, △E=△U Q=△U+W δQ=dU+δW q=△u+w δg=du+δw 思 第一定律第一解析式一 热→功的基本表达式 福

7 2–4 闭口系基本能量方程式     2 1 tot δ δ Q E j j i i e m e m W           闭口系， δ 0 δ 0 mi  mj  忽略宏观动能Uk和位能Up， E  U δ d δ δ d δ Q U W Q U W q u w q u w           第一定律第一解析式— 热 功的基本表达式

讨论： Q=AU+W δQ=dU+δW 9=△u+w δg=du+òw 1)对于可逆过程 δQ=dU+pdW 2)对于循环 ∮δ0=∮dU+∮δW→0t=Wn 超 3)对于定量工质吸热与升温关系，还取决于W的 “+”、“_”、 数值大小

8 讨论： 1）对于可逆过程 δQ  dU  pdV 2）对于循环 net net  δQ   dU   δW  Q  W 3）对于定量工质吸热与升温关系，还取决于W 的 “+” 、 “–” 、数值大小。 δ d δ δ d δ Q U W Q U W q u w q u w          

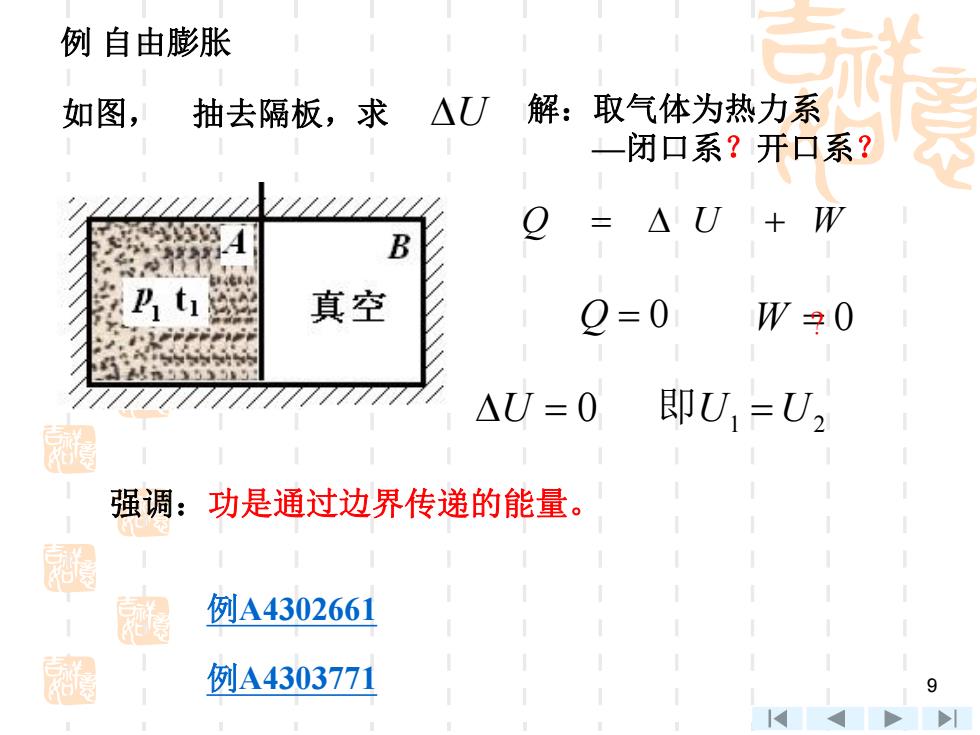
例自由膨胀 如图， 抽去隔板，求△U解：取气体为热力系 一闭口系？开口系？ =△U W 真空 Q=0 W孕0 △U=0 即U=U2 强调：功是通过边界传递的能量。 墨 雨 例A4302661 超 例A4303771 9

9 例 自由膨胀 如图， U 解：取气体为热力系 —闭口系？开口系？ Q   U  W 1 2 U  0 即U U 强调：功是通过边界传递的能量。 抽去隔板，求 W ? 0 例A4302661 例A4303771 Q  0

归纳热力学解题思路 1)取好热力系； 2)计算初、终态； 从已知条件逐步推向目标 3)两种解题思路 从目标反过来缺什么补什么 4)不可逆过程的功可尝试从外部参数着手。 周 超 10

10 归纳热力学解题思路 1）取好热力系; 2）计算初、终态; 3）两种解题思路 从已知条件逐步推向目标 从目标反过来缺什么补什么 4）不可逆过程的功可尝试从外部参数着手