
第四章 气体和蒸汽的基本的热力过程 Basic thermodynamic process 4-1研究热力过程的目的及一般方法 4-2理想气体的定压、定容和定温过程 43理想气体等比熵(可逆绝热)过程 4-4理想气体多变过程 45水蒸气的基本过程 超
1 第 四 章 气体和蒸汽的基本的热力过程 Basic thermodynamic process 4-1 研究热力过程的目的及一般方法 4-2 理想气体的定压、定容和定温过程 4-3 理想气体等比熵(可逆绝热)过程 4-4 理想气体多变过程 4-5 水蒸气的基本过程
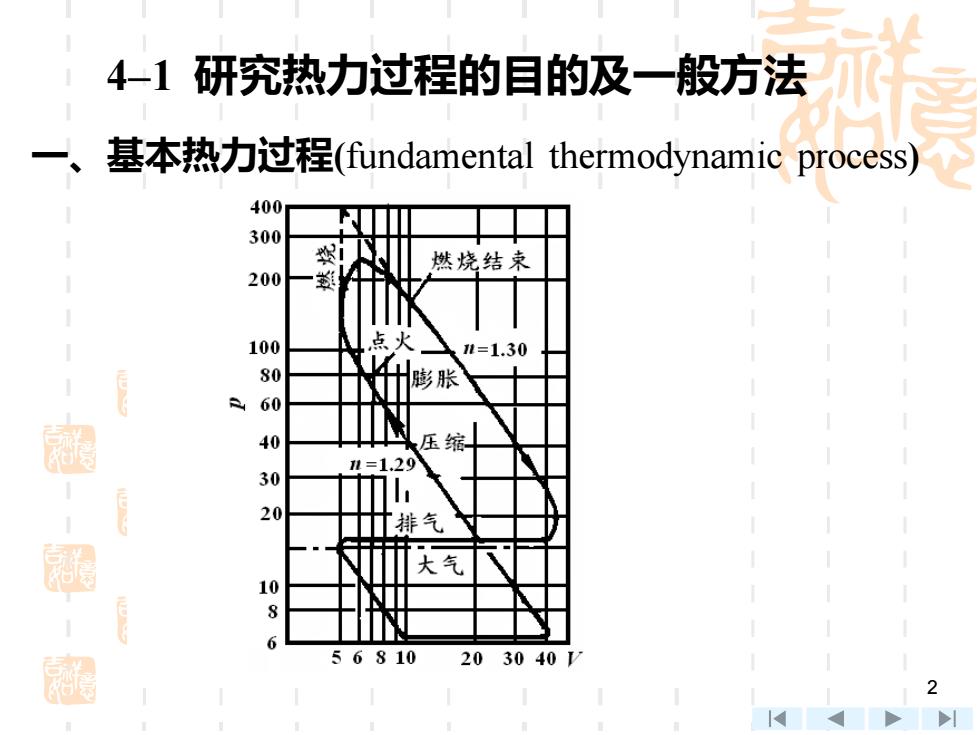
411 研究热力过程的目的及一般方法 一、 基本热力过程(fundamental thermodynamic process) 400 300 燃烧结束 200 100 点火 l=1.30 计膨胀 60 40 压缩 30 =1.29 20 排气 大气 10 8 6 5 6810 203040V 2
2 4–1 研究热力过程的目的及一般方法 一、基本热力过程(fundamental thermodynamic process)

在logp-logV图上有logp=-ln件c →pv”=常数 n=0 p=常数 定压过程 (isobaric process;constant pressure process) n=1 pN=常数 定温过程 (isothermal process;constant temperature process) n=K pv=常数 定熵(可逆绝热)过程 (isentropic process;reversible adiabatic process) n=士oo v=常数 定容过程 (isometric process;constant volume process) =常数 多变过程(polytropic process) 3
3 在log p-logV 图上有log p=-nlnV+c n = pv n p = = 0 常数 定压过程 =常数 多变过程(polytropic process) n pv n pv = = 1 常数 定温过程 n pv ( = = 常数 定熵 可逆绝热)过程 n v = =常数 定容过程 (isobaric process; constant pressure process) (isometric process; constant volume process) (isentropic process; reversible adiabatic process) (isothermal process; constant temperature process) 常数

二、 研究热力过程的目的、方法 1.目的 以热力学第一定律为基础,理想气体为工质,分析可逆 的基本热力过程中能量转换、传递关系,揭示过程中工质状 态参数的变化规律及热量和功量的计算。 2.方法和手段 求出过程方程及计算各过程初终态参数。 根据第一定律及理想气体性质计算过程中功和热。 画出过程的p-v图及T-s图,帮助直观分析过程中 参数间关系及能量关系。 O 可用的公式
4 1.目的 以热力学第一定律为基础,理想气体为工质,分析可逆 的基本热力过程中能量转换、传递关系,揭示过程中工质状 态参数的变化规律及热量和功量的计算。 2.方法和手段 求出过程方程及计算各过程初终态参数。 根据第一定律及理想气体性质计算过程中功和热。 画出过程的p-v图及T-s图,帮助直观分析过程中 参数间关系及能量关系。 可用的公式。 二、研究热力过程的目的、方法

Au=c片AT1Ah=c片AT1As=s9-s”-R1nB q=△u+w 9=△h+w 程
5 2 1 t V t = u c T 2 1 t p t = h c T 0 0 2 2 1 g 1 ln p s s s R p = − − 2 1 w p v = d 2 t 1 w v p = − d 2 1 q T s = d q u w = + t q h w = +

4-2理想气体的定压、定容和定温过程 一、 过程方程 定容过程(=常数) n=士oo V-V2 y1= RT V2= R王 P P2 TL 图 定压过程(p-常数) n=0 P=P2 雨 A飞? P2= R王 阔 y V2 6 K
6 4–2 理想气体的定压、定容和定温过程 一、过程方程 定容过程(v=常数) 1 2 n v v = = 定压过程(p=常数) 1 2 n p p = = 0 g 1 g 2 1 2 1 2 1 2 1 2 R T R T v v p p v v T T = = = g 1 g 2 1 2 1 2 1 2 1 2 R T R T p p v v p p T T = = =

定温过程 n=1 T=T T- 乃= R R PIV=P2V2 二、在p-v图及T-s图上表示 斜率 py" =常数 电+nd=0 dv - 团 Tds=δq=cndT T 圈 2 Cn
7 定温过程 1 2 n T T = = 1 二、在p – v 图及T – s 图上表示 n n p T v s d δ d T s q c T = = n n pv = 常数 1 1 2 2 1 2 1 1 2 2 g g p v p v T T p v p v R R = = = 斜率 n n T T s c = d d 0 p v n p v + = n p p n v v = −
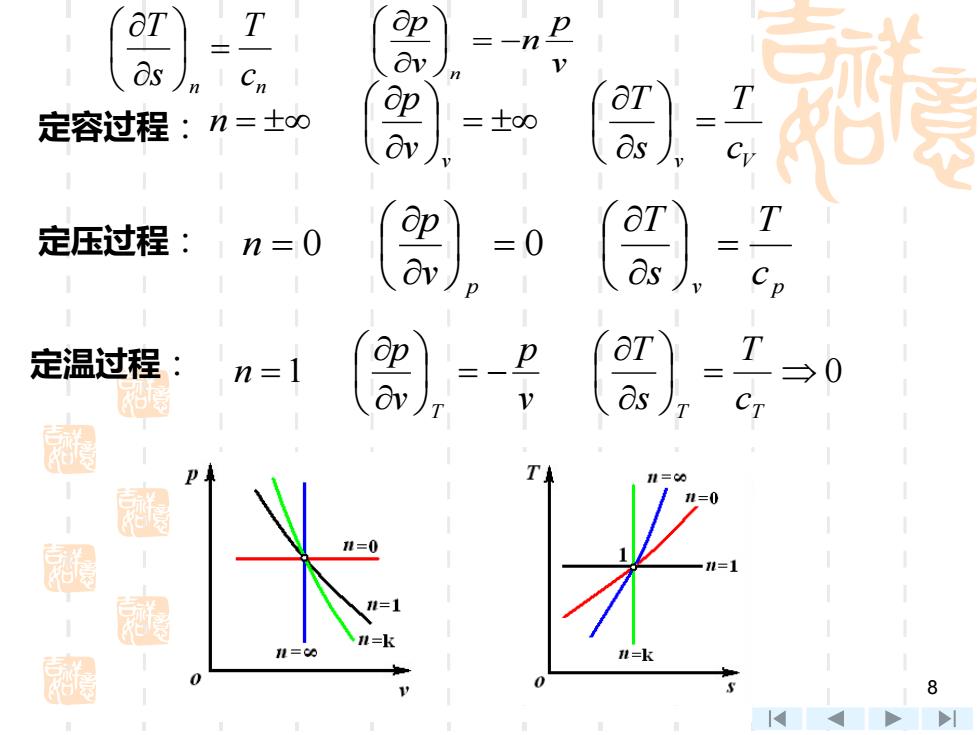
=-n P 8s Cn 定容过程:n=±oo =士o0 as 定压过程 1n=0 ) T =0 Cp 定温过程: T n=1 P → CT 图 1t=k 8 >l
8 定容过程 : 定压过程 : 定温过程 : v v V cT sT vp n = = = p v p cT sT vp n = = = 0 0 1 = 0 = − = T T T cT sT vp vp n n n cT sT = vp n vp n = −

三、比热容 定容过程 定压过程 定温过程 Rg Cy= y-1 Cp= R y-1 Cr→∞ 四、 △u、△h和△s 周 定容过程 冠 Au=cv(-) △h=cF(T-T) 超 a-小ga呀
9 三、比热容 定容过程 定压过程 定温过程 −1 = g V R c p Rg c −1 = cT → 四、Δu、 Δh和Δs 定容过程 ( ) ( ) 2 2 1 1 2 1 2 1 T T V T p T = − = − u c T T h c T T 2 2 1 1 d ln V V T T s c s c T T = =

定压过程 Au=c|F(g-T))△h=cF(I,-I) ge吃 定温过程 △M=01 △h=0 -小c罗h2→d=Rn的 超 10
10 定压过程 2 2 1 1 d ln p p T T s c s c T T = = 定温过程 2 2 2 g g 1 1 1 0 0 d ln ln V u h T v v s c R s R T v v = = = + = ( ) ( ) 2 2 1 1 2 1 2 1 T T V T p T = − = − u c T T h c T T