
第三章气体和蒸气的性质 Properties of gas and vapor 3-1理想气体 3-2理想气体的比热容 33理想气体的热力学能、焓和熵 3-4饱和状态、饱和温度和饱和压力 35水的定压加热汽化过程 3-6水和水蒸气状态参数 3-7水蒸气图表和图
1 第三章 气体和蒸气的性质 Properties of gas and vapor 3-1 理想气体 3-2 理想气体的比热容 3-3 理想气体的热力学能、焓和熵 3-4 饱和状态、饱和温度和饱和压力 3-5 水的定压加热汽化过程 3-6 水和水蒸气状态参数 3-7 水蒸气图表和图

3-1理想气体 理想气体(perfect gas or ideal gas)的基本假设 0分子为不占体积的弹性质点 除碰撞外分子间无作用力 → u=u(T) 理想气体是实际气体在低压高温时的抽象。 理想气体的状态方程(ideal-gas equation) PY=RgT 1kg =mRT→ pV=nRT n mol m3 PoVo RTo 1mol标准状态 Pa 气体常数,单位为J/kgK)R=MRg-8.3145J/(moK) 2
2 3-1 理想气体 分子为不占体积的弹性质点 除碰撞外分子间无作用力 u = u(T) 理想气体是实际气体在低压高温时的抽象。 一、理想气体(perfect gas or ideal gas)的基本假设 g pV mR T = g 0 0 0 1kg mol 1mol pv R T pV nRT n p V RT = = = 标准状态 Pa m3 kg 气体常数,单位为J/(kg·K) K R=MRg=8.314 5 J/(mol·K) 二、理想气体的状态方程(ideal-gas equation)
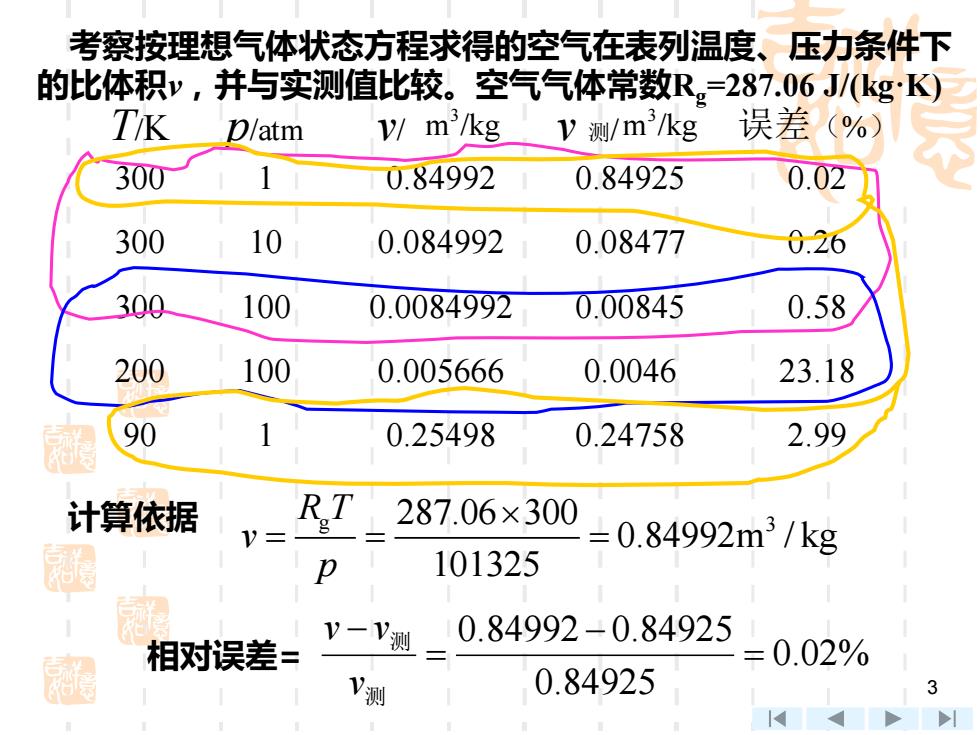
考察按理想气体状态方程求得的空气在表列温度、压力条件下 的比体积v,并与实测值比较。空气气体常数R。=287.06J/(kg:K) TK D/atm /m/kgy测/m/kg 误差(%) 300 1 0.84992 0.84925 0.02 300 10 0.084992 0.08477 0.26 300 100 0.0084992 0.00845 0.58 200 100 0.005666 0.0046 23.18 90 0.25498 0.24758 2.99 计算依据 V= RT 287.06×300 =0.84992m3/kg p 101325 0.84992-0.84925 相对误差= V一V测 =0.02% V测 0.84925 3
3 考察按理想气体状态方程求得的空气在表列温度、压力条件下 的比体积v,并与实测值比较。空气气体常数Rg=287.06 J/(kg·K) g 287.06 300 3 0.84992m / kg 101325 R T v p = = = 计算依据 相对误差= 0.02% 0.84925 0.84992 0.84925 = − = − 测 测 v v v T/K p/atm v/ 3 m /kg v 测/ 3 m /kg 误差(%) 300 1 0.84992 0.84925 0.02 300 10 0.084992 0.08477 0.26 300 100 0.0084992 0.00845 0.58 200 100 0.005666 0.0046 23.18 90 1 0.25498 0.24758 2.99

(1)温度较高,随压力增大,误差增大: (2)虽压力较高,当温度较高时误差还不大,但温度较低 则误差极大: (3)压力低时,即使温度较低误差也较小。 本例说明:低温高压时,应用理想气体假设有较大误差。 例A411133 讨论理想气体状态方程式 思 密
4 (1)温度较高,随压力增大,误差增大; (2)虽压力较高,当温度较高时误差还不大,但温度较低, 则误差极大; (3)压力低时,即使温度较低误差也较小。 本例说明:低温高压时,应用理想气体假设有较大误差。 例A411133 讨论理想气体状态方程式

3-2理想气体的比热容 一、 比热容(specific heat)定义和分类 c与过程有关 定义:c=lim 9 δg △7-0△T -d7 c是温度的函数 分类: 质量热容(比热容)cJ/(kgK) (specific heat capacity per unit of mass) 体积热容 C"J/(Nm3.K) Cm Mc 按物量 (volumetric specific heat capacity) =0.0224C 制 摩尔热容 Cm J/(mol-K) (mole specific heat capacity) 注:Nm3为非法定表示法,标准表示法为“标准m3”。 5
5 3–2 理想气体的比热容 一、比热容(specific heat)定义和分类 定义: 0 δ lim T d q q c → T T = = c与过程有关 c是温度的函数 分类: 按物量 质量热容(比热容)c J/(kg·K) (specific heat capacity per unit of mass) 体积热容 C' J/(Nm3·K) (volumetric specific heat capacity) 摩尔热容 Cm J/(mol·K) (mole specific heat capacity) m ' 0.0224 C Mc C = = 注: Nm3为非法定表示法,标准表示法为“标准m3”

质量定压热容(比定压热容) p,m> (constant pressure specific heat capacity per unit of mass) 及 按过程 质量定容热容(比定容热容) (constant volume specific heat capacity per unit of mass) 二、 理想气体比定压热容,比定容热容和迈耶公式 调 1.比热容一般表达式 du+δw du pdv (A) dT dT dT dT u=u(T,v) du= dT+ 6
6 按过程 质量定压热容(比定压热容) (constant pressure specific heat capacity per unit of mass) 质量定容热容(比定容热容) (constant volume specific heat capacity per unit of mass) V p c c 及 ' ,m ' ,m , , p p V V C C C C 二、理想气体比定压热容,比定容热容和迈耶公式 δ d δ d d ( ) d d d d q u w u p v c A T T T T + = = = + ( , d d d ) v T u u u u T v u T v T v = = + 1.比热容一般表达式
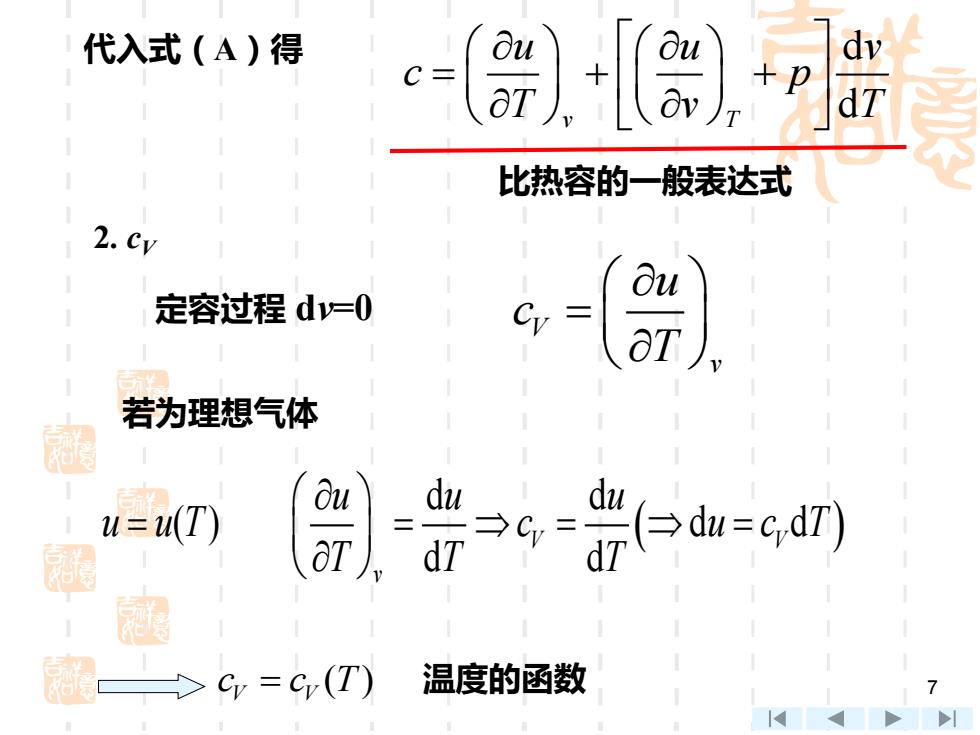
代入式(A)得 +P 比热容的一般表达式 2.cy 定容过程d=O 若为理想气体 Bu du u=(T) 围 dT 40加=6dn 1 c=,(T) 温度的函数
7 2. cV 定容过程 dv=0 V v u c T = 若为理想气体 ( ) d d ( ) d d d d V V v u u u u u T c u c T T T T = = = = c c T V V = ( ) 温度的函数 代入式(A)得 d v T d u u v c p T v T = + + 比热容的一般表达式

3.Cp 据一般表达式 dv dT 若为理想气体 u=f(T) =0→ =0 dv p=Cy+p du pdyd(h-py)+pdy dh-vdp dT dT dT dT dT 圈 Cp= (pdh=c,dr)→c,=c,(T) 阔 c是温度函数 8
8 3. cp 据一般表达式 d d d d p V v T T u u v u v c p c p T v T v T = + + = + + 若为理想气体 ( ) 0 T u u f T v = = d d d d d d d ( ) d d d d d p V v u p v h v p h pv p v c c p T T T T T − + − = + = + = = d 0 p = ( ) d d d d p p h c h c T T = = cp是温度函数 ( ) p p c c T =

4.Cp-Cv dh-du d(u+pv)-du Cp- Cy= dT dT d(u+RT)-du R dT 周 Cp-cy Rg 迈耶公式(Mayer's formula) 5.讨论 I)c,与cv均为温度函数,但c,-c恒为常数:Rg 9
9 4. cp- cV ( ) ( g ) g d d d d d d d d d p V h u u pv u c c T T u R T u R T − + − − = = + − = = p V g c c R − = 迈耶公式(Mayer’s formula) 5. 讨论 1) cp与cV均为温度函数,但cp–cV恒为常数:Rg
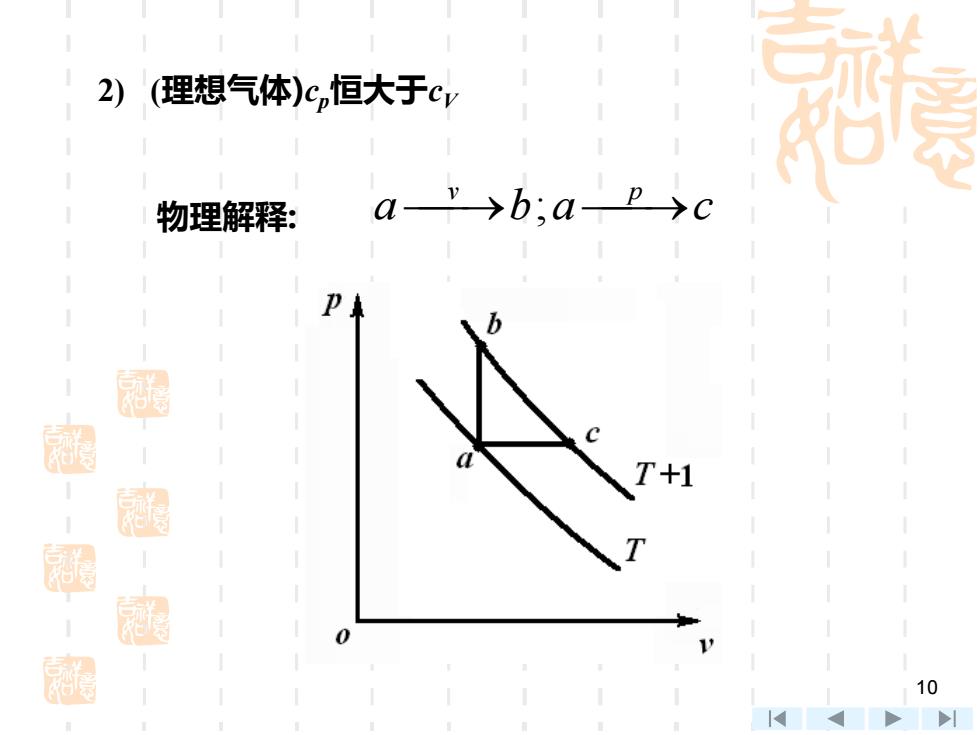
2) (理想气体)c,恒大于cv 物理解释: a→b;ap>c T+1 10
10 2) (理想气体)cp恒大于cV 物理解释: a b a c ⎯v → ; ⎯p →