《电力系统分析》课程教学课件（讲稿）11 电力系统不对称故障的分析和计算

第八章电力系统不对称故障的分析和计算 8-1简单不对称短路的分析 -正序等效定则（重点） 8-2电压和电流对称分量经变压器后的相位变换 8-3非全相断线的分析

8-1 简单不对称短路的分析 –正序等效定则（重点） 8-2 电压和电流对称分量经变压器后的相位变换 8-3 非全相断线的分析 第八章 电力系统不对称故障的分析和计算

8-1.简单不对称短路的分析计算 ·当网络元件只用电抗表示时，不对称短路的序网络方程 Es -iaZis =Val Es jXilal =Val 0-ia2Z2x='2 -jXxio2=Va2 O-iaoZos=Vao -jXoxino Vuo 该方程组有三个方程，但有六个 未知数，必须根据边界条件列出 另外三个方程才能求解

8-1. 简单不对称短路的分析计算 • 当网络元件只用电抗表示时，不对称短路的序网络方程           0 0 0 2 2 2 1 1 1 0 0 a a a a a a I Z V I Z V E I Z V                           0 0 0 2 2 2 1 1 1 a a a a a a jX I V jX I V E jX I V        该方程组有三个方程，但有六个 未知数，必须根据边界条件列出 另外三个方程才能求解

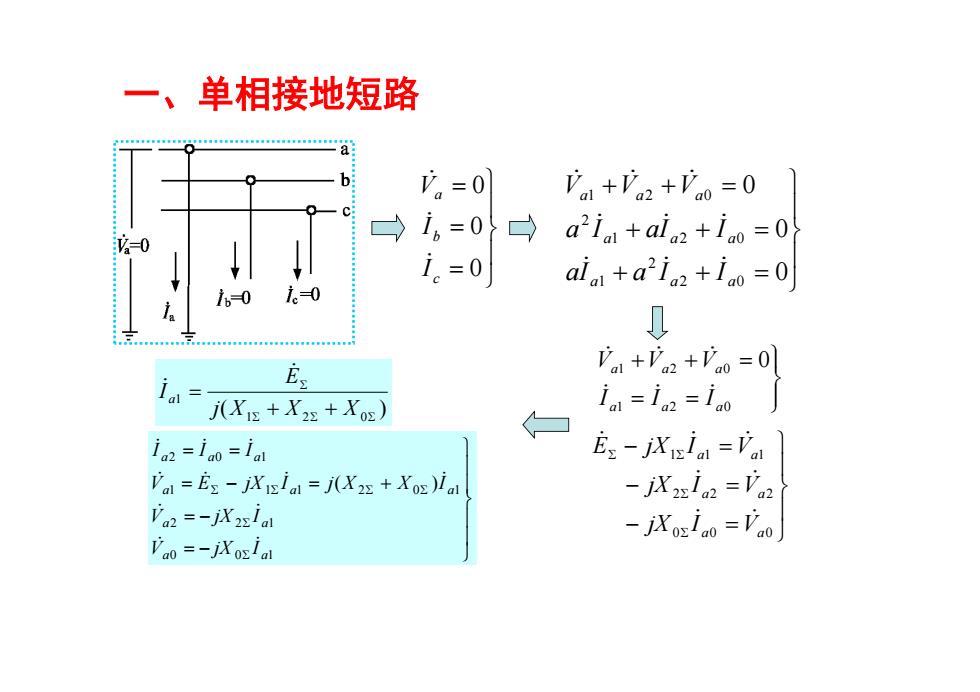
一、单相接地短路 。=0 a+'a2+广o=0 →i6=0 日a2 ia +ain2+io=0 = i。=0 ala+a2in2+ia=0 i。0 i0 0 E a+'2+=0 j(Xi+X2:+Xo) ia=1n2=1a0 1a2 =ia0=ial E2-jXia=广a】 Val =Es -jXiial=j(X2s Xo)ial -jXxin =Vn Va2=-jX2ial -jXoziao Vao Vao=-jXoslal

一、单相接地短路         0 0 0 c b a I I V                  0 0 0 2 0 2 1 1 2 0 2 1 2 0 a a a a a a a a a aI a I I a I aI I V V V                   1 2 0 1 2 0 0 a a a a a a I I I V V V                      0 0 0 2 2 2 1 1 1 a a a a a a jX I V jX I V E jX I V        ( ) 1 2 0 1        j X X X E I a                        0 0 1 2 2 1 1 1 1 2 0 1 2 0 1 ( ) a a a a a a a a a a V jX I V jX I V E jX I j X X I I I I           

复合序网 电压和电流的各序分量，可以直接用复合序网来求得。 根据故障处各序量之间的关系，将各序网络在故障 端口联接起来所构成的网络称为复合序网

复合序网 电压和电流的各序分量，可以直接用复合序网来求得。 根据故障处各序量之间的关系，将各序网络在故障 端口联接起来所构成的网络称为复合序网

单相接地故障的复合序网 pa+广an2+'o=0 ia=in=1ao E2-jⅸzi=V -jX:i.=Va -jXzi。= E j(Xis +X2z+Xos) 1a2=ia0=la Va =Es -iXzial=j(X2x Xoz)ia 1 Va2=-jX22lal jXox Vao=-jXolal Va

         1 2 0 1 2 0 0 a a a a a a I I I V V V                      0 0 0 2 2 2 1 1 1 a a a a a a jX I V jX I V E jX I V        单相接地故障的复合序网 ( ) 1 2 0 1        j X X X E I a                        0 0 1 2 2 1 1 1 1 2 0 1 2 0 1 ( ) a a a a a a a a a a V jX I V jX I V E jX I j X X I I I I           

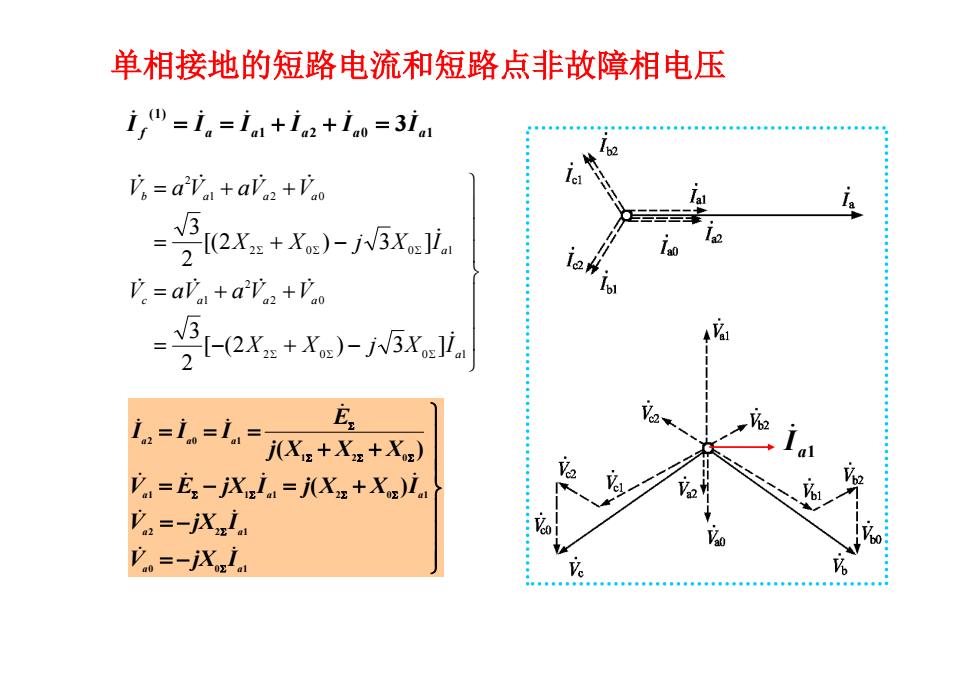
单相接地的短路电流和短路点非故障相电压 i =i,=in+in+in=3in V=aVa+aV+Vo 2[(2X::+Xw)-j3Xli '.=an+a2Y.2+'o -92x+a)-w5x E 1=i=1=ix.+X+X.） V.=E:-jXi.=j(X+X)i. V=-jXl 。=-jXza

单相接地的短路电流和短路点非故障相电压 1 2 0 1 (1) f a a a a 3 a I I I I I I                                    2 0 0 1 2 0 2 1 2 0 0 1 1 2 0 2 [ (2 ) 3 ] 2 3 [(2 ) 3 ] 2 3 a c a a a a b a a a X X j X I V aV a V V X X j X I V a V aV V                                      0 0 1 2 2 1 1 1 1 2 0 1 1 2 0 2 0 1 ( ) ( ) a a a a a a a a a a V jX I V jX I V E jX I j X X I j X X X E I I I             a1 I 

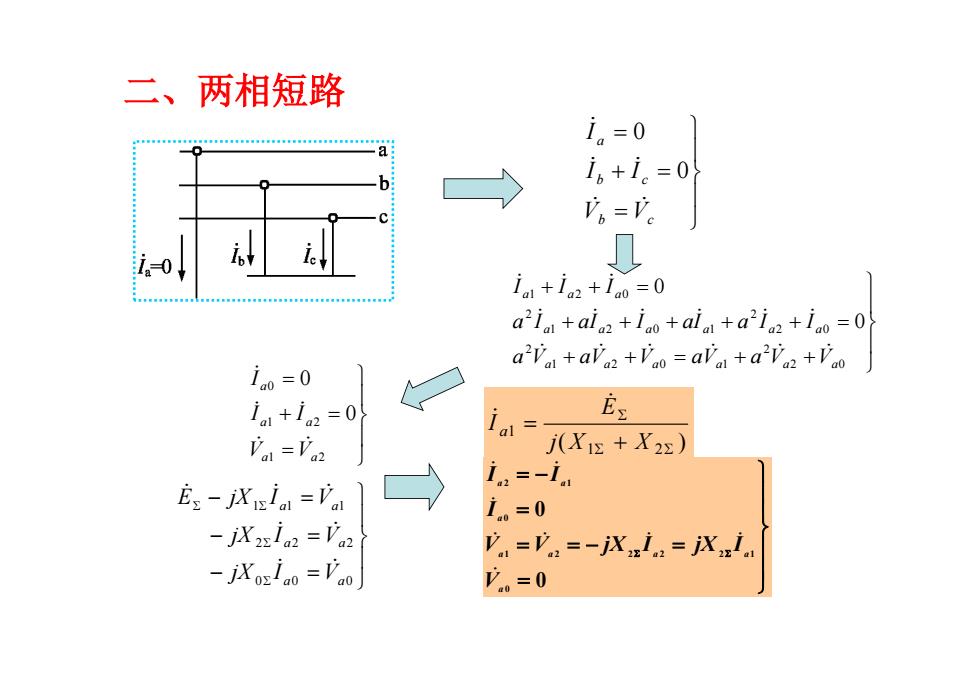
二、两相短路 i=0 i6+i。=0 。= -0 0 a2ia +aln+ino+ala +a2ia+ia=0 a'Va +alaz+Vao=ala +a"Vaz+Vao ino=0 i+i2=0 Es n1=广2 j(Xi +X2x) Es jXia =Va i.=-1. i.=0 -jXsi2=乃n2 V=y:=-jⅸ1=jX1. -jXoloo=Vao .=0

               0 0 0 2 2 2 1 1 1 a a a a a a jX I V jX I V E jX I V        二、两相短路          b c b c a V V I I I      0 0                    2 0 2 1 2 0 1 2 2 0 2 1 2 0 1 2 1 2 0 0 0 a a a a a a a a a a a a a a a a V aV V aV a V V a I aI I aI a I I I I I                         1 2 1 2 0 0 0 a a a a a V V I I I      ( ) 1 2 1      j X X E I a                  0 0 0 1 2 2 2 2 1 0 2 1 a a a a a a a a V V V jX I jX I I I I        

两相短路的复合序网 in0=0 ia+in2 =0 a=2 Ex -jXzia =Vat -jX2sio2 =Vo2 ix① -jXozlao=Vao Ia= Es j(Xi +X2:) i,=-i i。=0 =.=-j1=j 。=0

         1 2 1 2 0 0 0 a a a a a V V I I I                     0 0 0 2 2 2 1 1 1 a a a a a a jX I V jX I V E jX I V        两相短路的复合序网 ( ) 1 2 1      j X X E I a                  0 0 0 1 2 2 2 2 1 0 2 1 a a a a a a a a V V V jX I jX I I I I        

两相短路的短路电流 i,=a2ial +ala2+ia0 =(a2-a)ia =-j3ial i。=-i6=jn3ial I2=16=1e=31ai E lae十短 Ia2 =-ia Va =Va2=-iX2xio2=jX2xia

两相短路的短路电流               1 1 1 2 1 2 0 2 3 ( ) 3 c b a b a a a a a I I j I I a I aI I a a I j I          1 (2) f b c 3 a I  I  I  I ( ) 1 2 1      j X X E I a             1 2 2 2 2 1 2 1 a a a a a a V V jX I jX I I I      

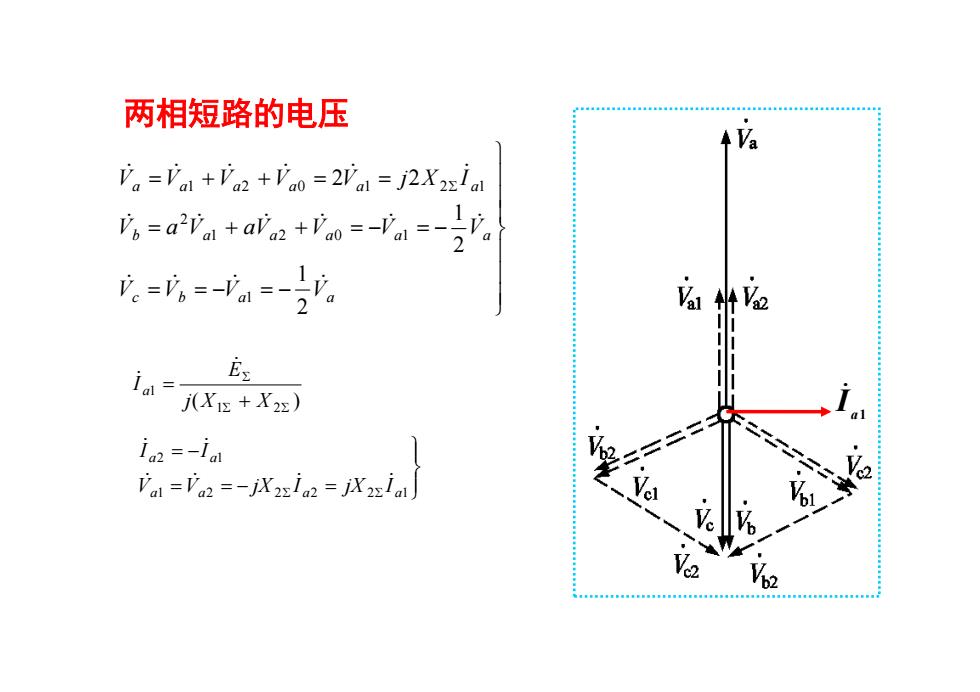
两相短路的电压 Va =Val +Va2 +Vao 2Val j2X2zial 店=a27m+aia+io=-'a=-p。 2 。=。=-a= 1。 ia=Xe+X2z） 1a2 =-ial Val =Va2 =-jX2xia2=jX2zial %2 2

两相短路的电压                        c b a a b a a a a a a a a a a a V V V V V a V aV V V V V V V V V j X I                 2 1 2 1 2 2 1 1 2 0 1 2 1 2 0 1 2 1 ( ) 1 2 1      j X X E I a             1 2 2 2 2 1 2 1 a a a a a a V V jX I jX I I I       a1 I 