
上游充通大学 SHANGHAI JIAO TONG UNIVERSITY Engineering Thermodynamics I Lectures 17 Chapter 5 Mass and Energy Analysis of Control Volume Analysis Spring,2017 Prof.,Dr.Yonghua HUANG 强 是a http://cc.sjtu.edu.cn/G2S/site/thermo.html 1日G
Engineering Thermodynamics I Lectures 17 Spring, 2017 Prof., Dr. Yonghua HUANG http://cc.sjtu.edu.cn/G2S/site/thermo.html Chapter 5 Mass and Energy Analysis of Control Volume Analysis
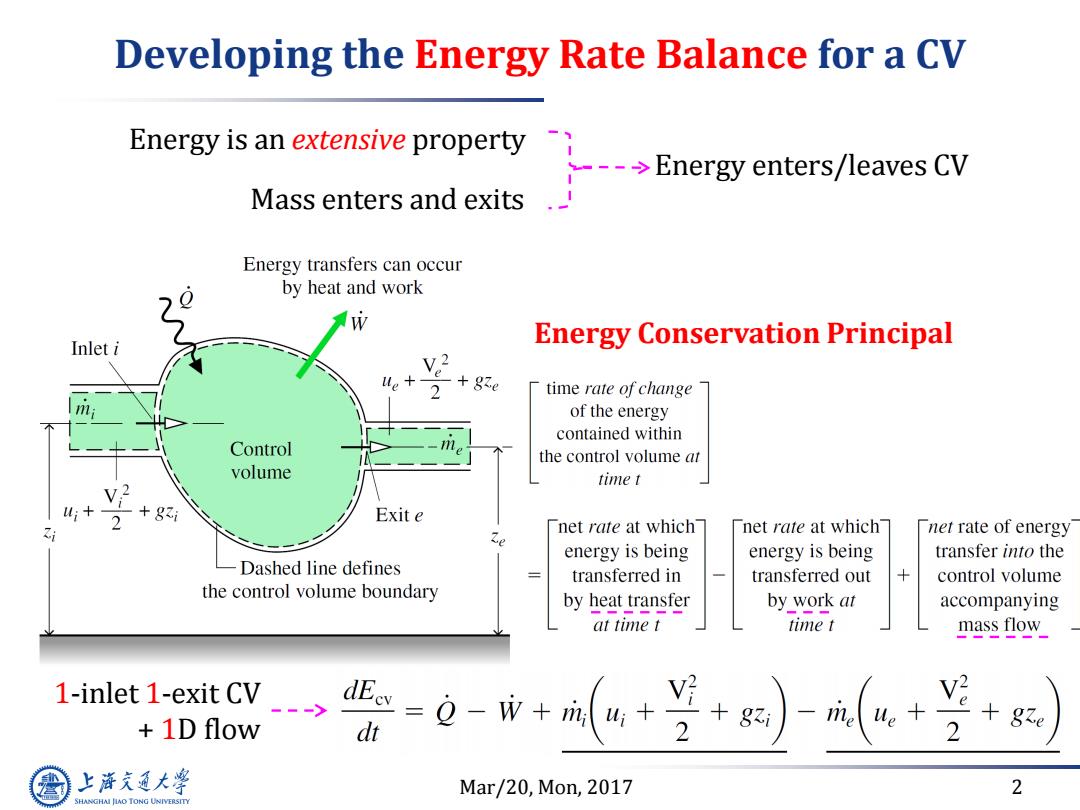
Developing the Energy Rate Balance for a CV Energy is an extensive property Energy enters/leaves CV Mass enters and exits. Energy transfers can occur by heat and work Inlet i Energy Conservation Principal time rate of change of the energy contained within Control the control volume at volume time t W; +8 Exit e net rate at which net rate at which net rate of energy energy is being energy is being transfer into the Dashed line defines transferred in transferred out 十 control volume the control volume boundary by heat transfer by work at accompanying at time t time t mass flow 1-inlet 1-exit CV> 1D flow =Q-+m4+ dt 2 +gzi me ue 2 上降文通大学 Mar/20,Mon,2017 2 SHANGHAI JLAO TONG UNIVERSITY
Mar/20, Mon, 2017 2 Developing the Energy Rate Balance for a CV Energy is an extensive property Mass enters and exits Energy enters/leaves CV Energy Conservation Principal 1-inlet 1-exit CV + 1D flow
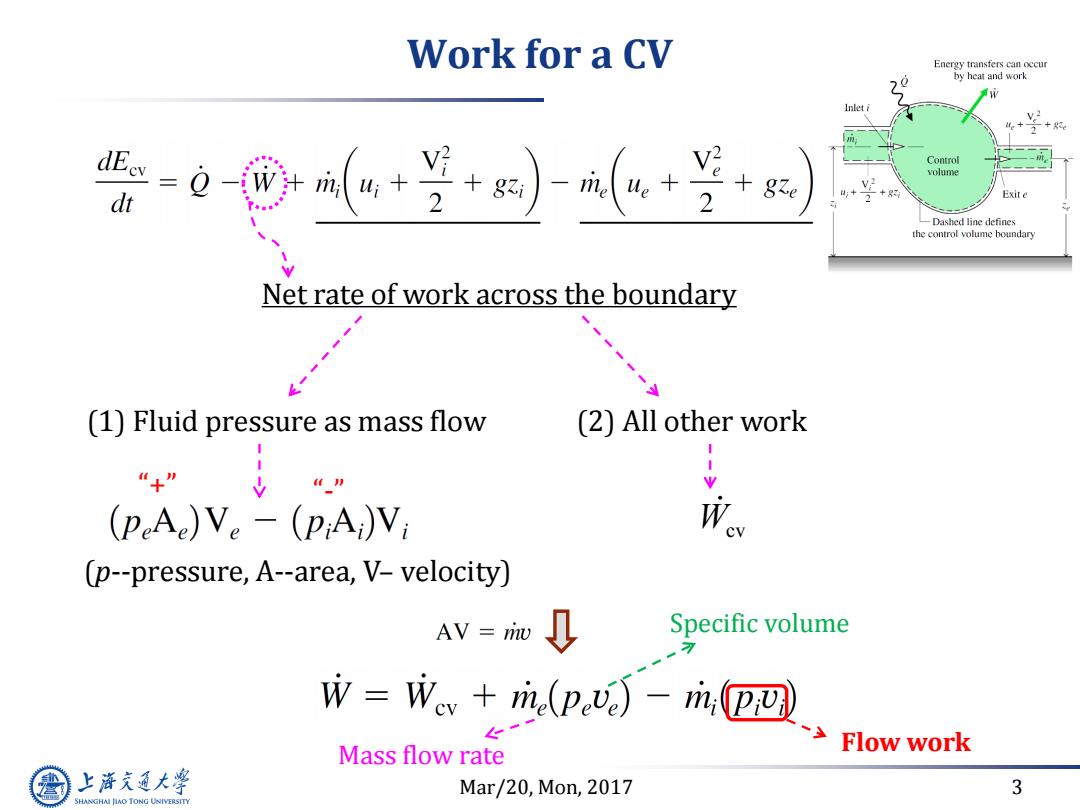
Work for a CV Energy transfers can occur by heat and work dE。=Q-w Control volume dt 2 + 2 + Exit e -Dashed line defines the control volume boundary Net rate of work across the boundary (1)Fluid pressure as mass flow (2)All other work “+” (peAe)Ve-(pA)V; We (p--pressure,A--area,V-velocity) AV riw Specific volume W=Wev+m(p)-m,D四 Mass flow rate Flow work 上游气通大粤 Mar/20,Mon,2017 3 SHANGHAI JLAO TONG UNIVERSITY
Mar/20, Mon, 2017 3 Work for a CV Net rate of work across the boundary (1) Fluid pressure as mass flow (2) All other work Wcv (p--pressure, A--area, V– velocity) “+” “-” Mass flow rate Specific volume Flow work
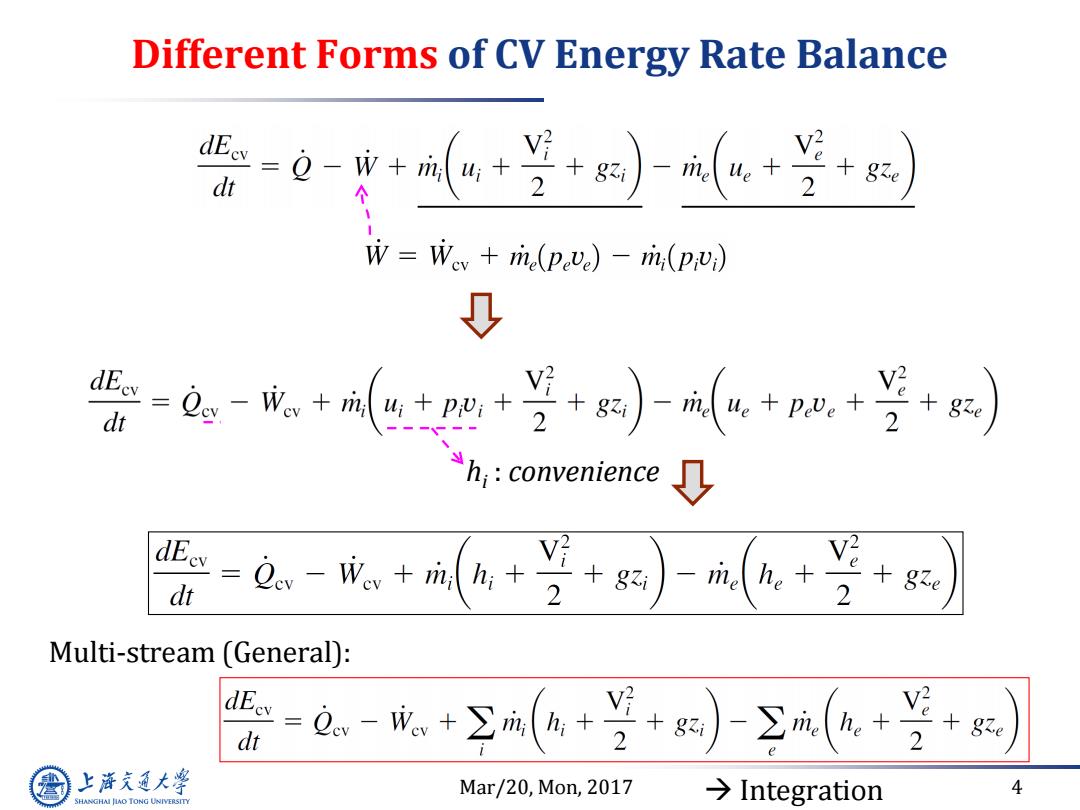
Different Forms of CV Energy Rate Balance 0- dt 个 W=Wv+m(pve)-m(p) 0 --++)+m+苦+) dt h:convenience dEey dt Lev-Wev+rin hi+ 2 +gi - rite he 2 Multi-stream (General): =a.-+Σa(6++)Σae-兰 dt 上降文通大学 Mar/20,Mon,2017 →Integration 4 SHANGHAI JIAO TONG UNIVERSITY
Mar/20, Mon, 2017 4 Different Forms of CV Energy Rate Balance hi : convenience Multi-stream (General): Integration

Example 17.1 CM vs.CV analysis Known: 0.15 m3 O2 cylinder,Initially t1=38 C,p=0.55 MPa,V=0.15m3. Pressure release valve:automatically open when p 0.7 MPa, ·Heating the O2: Find:2@To2=285℃ [R=260 J/(kgK);cy=657 J/(kgK);c=917 J/(kgK)] =0.15m 14138C 2 告285C 055M明CY 名0.7N亚 CV g0.7p 3 上游究通大学 Mar/20,Mon,2017 5 SHANGHAI JIAO TONG UNIVERSITY
Mar/20, Mon, 2017 5 Example 17.1 CM vs. CV analysis Known: • 0.15 m3 O2 cylinder, Initially t1=38 ℃, p1= 0.55 MPa, V=0.15m3 . • Pressure release valve: automatically open when p > 0.7 MPa, • Heating the O2 . Find: Q @ TO2 = 285 ℃ [R=260 J /(kg·K);cV = 657 J/(kg·K);cp= 917 J/(kg·K)]

Solution:Ideal gas model,Closed system 02: 20.15m2 138C R=260J/kg·K) 285℃ 月055M明 名0.7NMP CV 50.P 1 3 Cv=657J/(kg·K) cp=917J/(kg·K) 0.55×106Pa×0.15m3 =1.020kg RT 260J/(kg·K)×(273+38)K 0.7×106Pa×0.15m3 =0.274kg RT 260J/(kg·K)×(273+285)K 上游通大学 Mar/20,Mon,2017 6 SHANGHAI JLAO TONG UNIVERSITY
Mar/20, Mon, 2017 6 R 260 J/(kg K) 6 3 1 1 1 0.55 10 Pa 0.15 m 1.020 kg 260 J/(kg K) 273 38 K p V m RT 6 3 3 3 3 0.7 10 Pa 0.15 m 0.274 kg 260 J/(kg K) 273 285 K p V m RT O2 : 657 J/(kg K) V c 917 J/(kg K) p c Solution:Ideal gas model, Closed system

2:1→2 constant and m 015m 38C 2 3285C 055M-CV 名-0.7MP ,-BI= 0.7 MPa 50.乃r ×311K=395.82K =m. 0.55 MPa 2,=m,c(T3-T) =1.02kg×0.657J/(kgK)×(395.85-311)K=56.84kJ p:2>3 constant p,but not m δQ,=mc,dT 0-m-rg In- T R 917J/kg·K)×0.7×106Pa×0.15m3 (285+273)K xln =127.17kJ 260J/(kg·K) 395.82K Q=9+Q,=56.84kJ+127.17k=184.01kJ 上游充通大 Mar/20,Mon,2017 7 SHANGHAI JLAO TONG UNIVERSITY
Mar/20, Mon, 2017 7 QV:12 constant V and m 2 2 1 1 0.7 MPa 311 K 395.82 K 0.55 MPa p T T p 1 2 1 1.02 kg 0.657 J/(kg K) 395.85 311 K 56.84 kJ Q m c T T V V Qp:23 constant p, but not m δ d Q mc T p p 3 2 d T p p T Q mc T 6 3 917 J/(kg K) 0.7 10 Pa 0.15 m (285 273) K ln 127.17 kJ 260 J/(kg K) 395.82 K 56.84 kJ 127.17 kJ 184.01 kJ Q Q Q V p 3 2 3 3 3 2 d ln T p p T p V T c p V c T RT R T

Try another method: 38C F2850 -055 MPa- 4名-0.7MP Energy balance for open system: 0.7n4 Process 2-3:inlet-exit increment δQp-h.δm。=dU--→δQp=h.δm。+a(mu) =hδm。+mdu+udm Conservation of mass: δn。=-dm Atequimstate:he=h -md(h)dm=mic,dT-prdm m Integration: T m m T m2 = T RT, R 上游气通大粤 Mar/20,Mon,2017 8 SHANGHAI JLAO TONG UNIVERSITY
Mar/20, Mon, 2017 8 Energy balance for open system: Process 23: inlet – exit = increment δ δ d Q h m U p e e Conservation of mass: δ d m m e At equilibrium state: he =h δ d d d d Q m u h u m mc T pv m p V d d V pV pV c T m RT m δ δ d Q h m mu p e e δ d d e e h m m u u m Try another method: 3 3 2 2 3 3 2 2 d d ln ln T m V p V T m pV T m c T m Q c pV pV R T m R T m 3 3 3 p V m RT 3 3 2 ln p p c p V T Q R T 3 2 2 3 m T m T 2 2 2 p V m RT 3 2 p p p Integration:

Example 17.2 Prove:Ideal gas release process of a rigid adiabatic vessel obeys: K-1 Tp k =const Prove: Vessel as the CV,Energy balance 70 8Q-h.δ.=d(mu)) EoS:mR,T=pV 0 =const mdu+udm+hδm。=0 dm dT dp m T 灰=h=-咖 p ↓ mdu+udm-hom=0 dm dT 0 e m p T mcdT+c,Tdm-c,Tr∈0 0 0 Organize and 1 dT dp dT Integration K-1 Tp K k-1 T p T dT p k-1T 上游入上 Mar/20,Mon,2017 9 SHANGHAI JIAO TONG UNIVERSITY
Mar/20, Mon, 2017 9 Prove: Ideal gas release process of a rigid adiabatic vessel obeys: Tp const 1 Prove: e e δQ h m mu δ d( ) e h h m m δ d e e e m u u m h m d d δ 0 m u u m h m d d δ 0 Vessel as the CV, Energy balance Example 17.2 0 d d d 0 mc T c T m c T m V V p mc T c c T m V p V d d Tp c 1 mR T pV g 1 d d d 1 T p T T p T Organize and Integration EoS: d d d m p T m p T d d d d m T p V m T p V V constp T d 1 d 1 m T m T

Steady state Conservation of mass ∑m=∑m (mass rate in) (mass rate out) Conservation of energy 0 7 a-晚+(a+兰+)区a(+兰+x) dt a.+ya+兰+)-成+公e+誉+) (energy rate in) (energy rate out) 上游充通大学 Mar/20,Mon,2017 10 SHANGHAI JLAO TONG UNIVERSITY
Mar/20, Mon, 2017 10 Steady state 0 Conservation of mass Conservation of energy