
上岸充通大学 SHANGHAI JIAO TONG UNIVERSITY Engineering Thermodynamics I Lecture 32 Chapter 7 Entropy (Section 7.13) Spring,2017 福 Prof.,Dr.Yonghua HUANG 几nMA http://cc.sjtu.edu.cn/G2S/site/thermo.html 1日G
Engineering Thermodynamics I Lecture 32 Spring, 2017 Prof., Dr. Yonghua HUANG Chapter 7 Entropy (Section 7.13) http://cc.sjtu.edu.cn/G2S/site/thermo.html
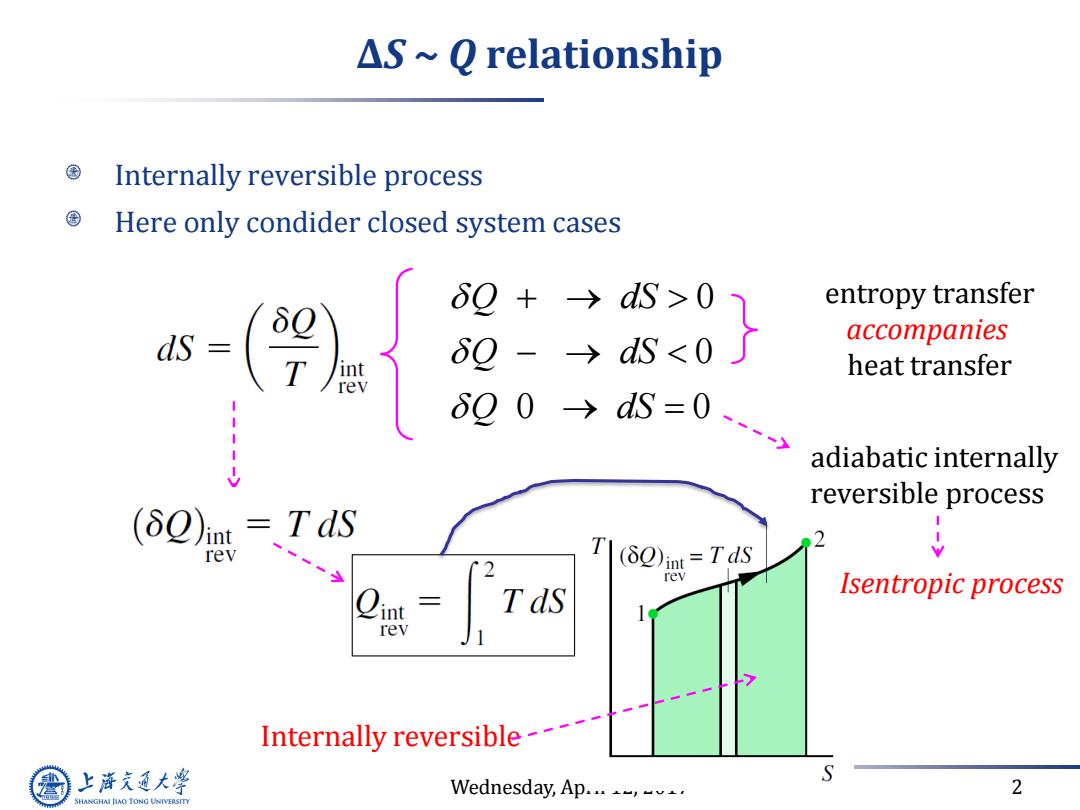
△S~Q relationship Internally reversible process Here only condider closed system cases 6Q+→dS>0 entropy transfer 6g-→dS<0 accompanies heat transfer 00→S=0y adiabatic internally reversible process (δQ)mt=TdS rev 2 T(2)in=Tds rev Tds Isentropic process rev Internally reversible--- 上游充通大 Wednesday,Ap...-,. 2 SHANGHAI JIAO TONG UNIVERSITY
Wednesday, April 12, 2017 2 ∆S ~ Q relationship Internally reversible process Here only condider closed system cases 0 0 0 0 Q dS Q dS Q dS entropy transfer accompanies heat transfer adiabatic internally reversible process Isentropic process Internally reversible
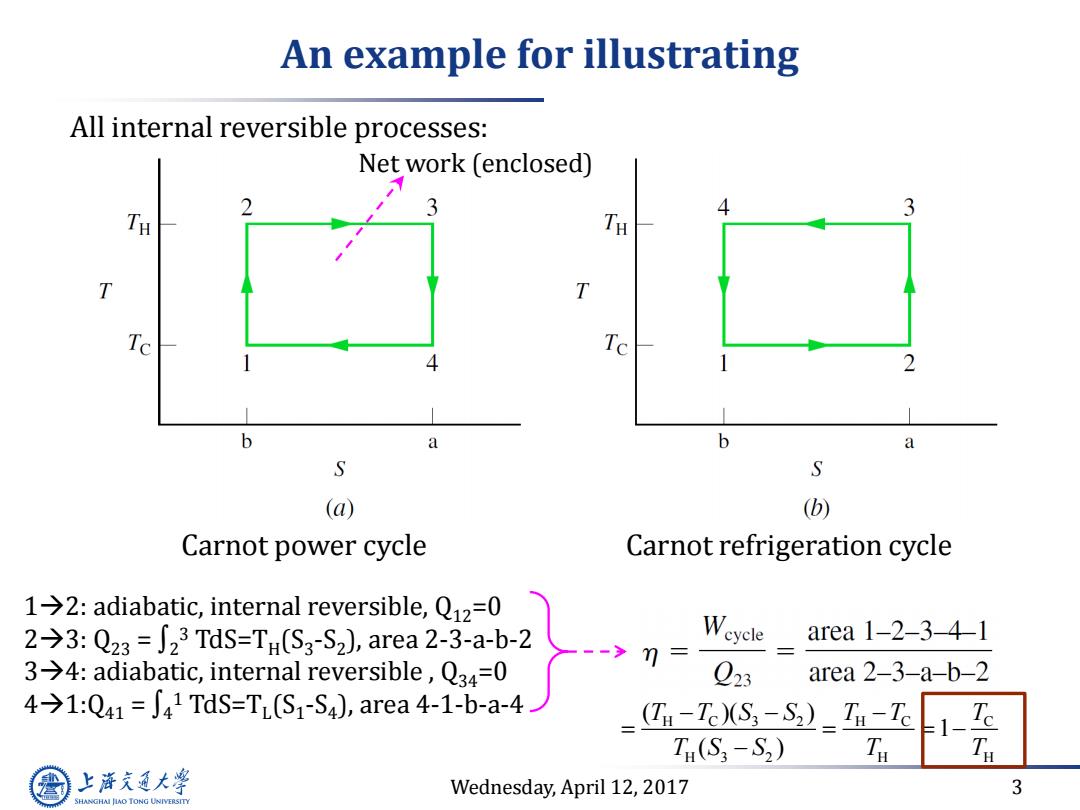
An example for illustrating All internal reversible processes: Net work (enclosed) TH TH Te 4 b a b a S S (a) (b) Carnot power cycle Carnot refrigeration cycle 1→2:adiabatic,internal reversible,Q12=0 2→3:Q23=∫23TdS=TH(S3-S2),area2-3-a-b-2 Weycle area1-2-3-41 3→4:adiabatic,internal reversible,Q34=0 7= Q23 area 2-3-a-b-2 4→1:Q41=J41TdS=T(S1-S4),area4-1-b-a-4 (Ta-Te)(S3-S2)Ti-Tc 1-工 T(S3-S2) Ta 上泽通大学 Wednesday,April 12,2017 3 SHANGHAI JLAO TONG UNIVERSITY
Wednesday, April 12, 2017 3 An example for illustrating Carnot refrigeration cycle 12: adiabatic, internal reversible, Q12=0 23: Q23 = ∫2 3 TdS=TH (S3 -S2 ), area 2-3-a-b-2 34: adiabatic, internal reversible , Q34=0 41:Q41 = ∫4 1 TdS=TL (S1 -S4 ), area 4-1-b-a-4 Carnot power cycle All internal reversible processes: Net work (enclosed) H C 3 2 H C C H 3 2 H H ( )( ) 1 ( ) T T S S T T T T S S T T
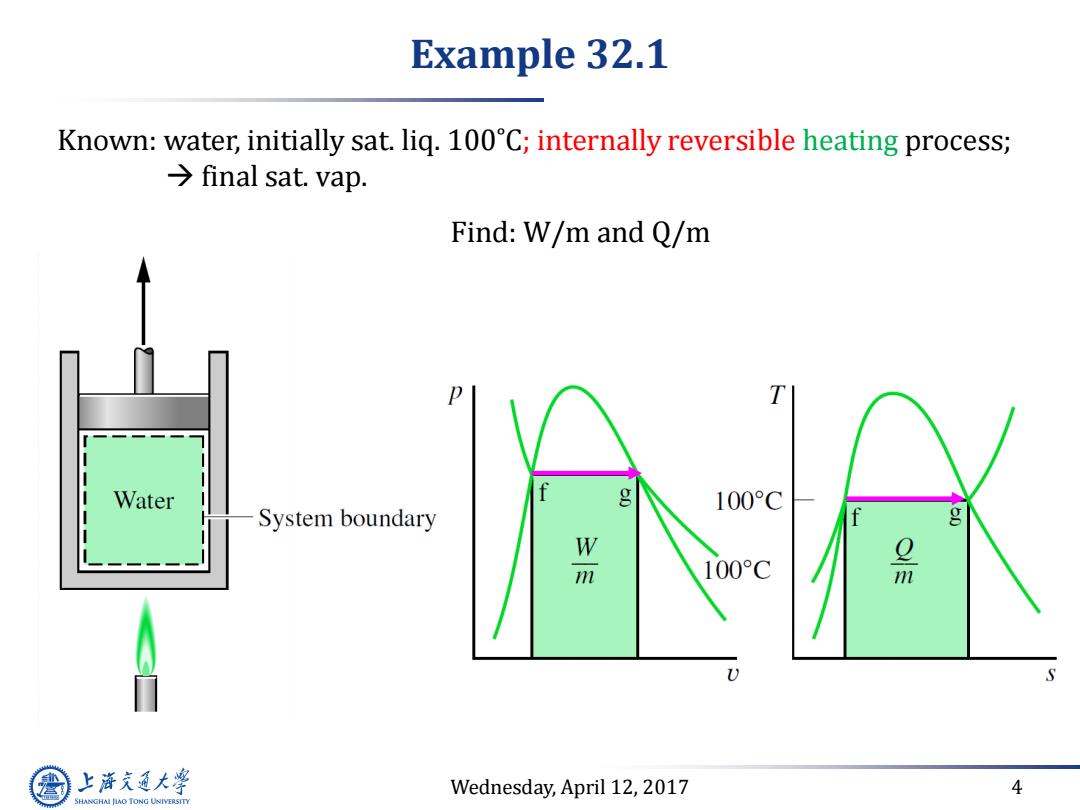
Example 32.1 Known:water,initially sat.liq.100C;internally reversible heating process; final sat.vap. Find:W/m and Q/m T Water g 100°C System boundary g 100°C m S 上游充通大 Wednesday,April 12,2017 4 SHANGHAI JIAO TONG UNIVERSITY
Wednesday, April 12, 2017 4 Example 32.1 Known: water, initially sat. liq. 100˚C; internally reversible heating process; final sat. vap. Find: W/m and Q/m
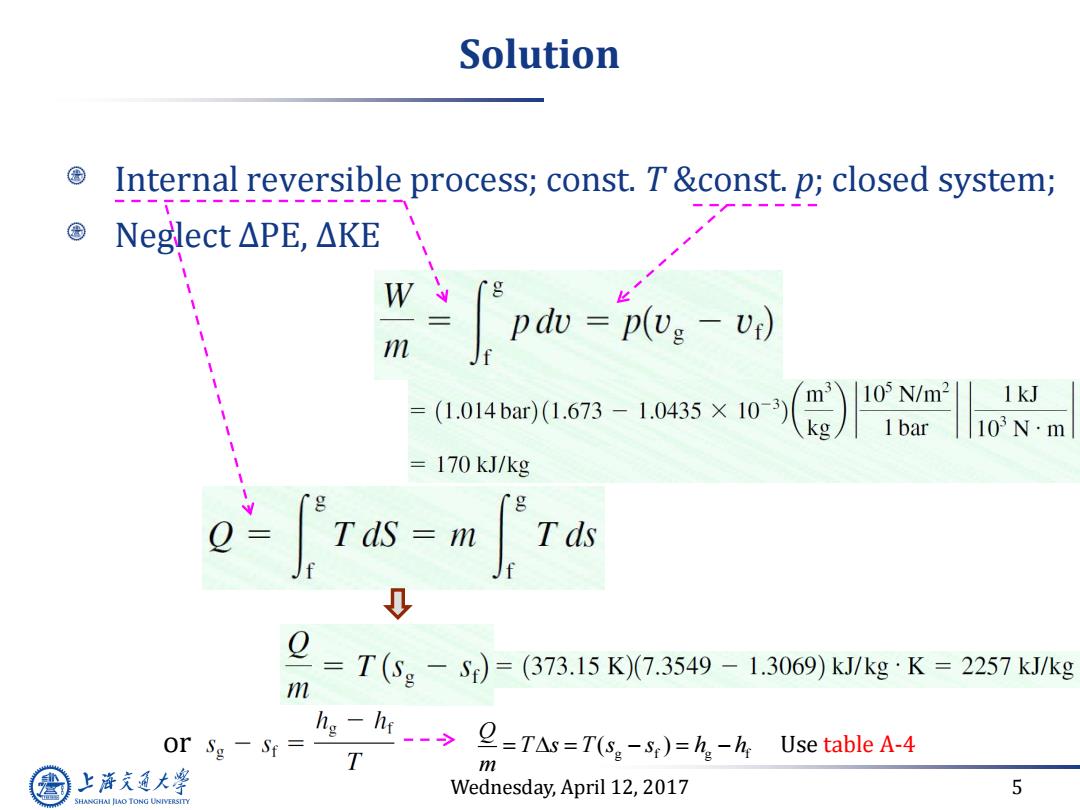
Solution Internal reversible process;const.T&const.p;closed system; Neglect△PE,△KE W m J pdo=plv:-v) (1.014bar)(1.673-1.0435×10-3) 1kJ = 103N·m =170 kJ/kg Tas-m Tds m =T(Sg-S)=(373.15K)(7.3549-1.3069)k/kgK=2257kkg or Sg-Sr= lighr2=TAs=T(s-5 )=hh Use table A-4 T m 上游充通大学 Wednesday,April 12,2017 5 SHANGHAI JLAO TONG UNIVERSITY
Wednesday, April 12, 2017 5 Solution Internal reversible process; const. T &const. p; closed system; Neglect ∆PE, ∆KE or g f g f ( ) Q T s T s s h h m Use table A-4
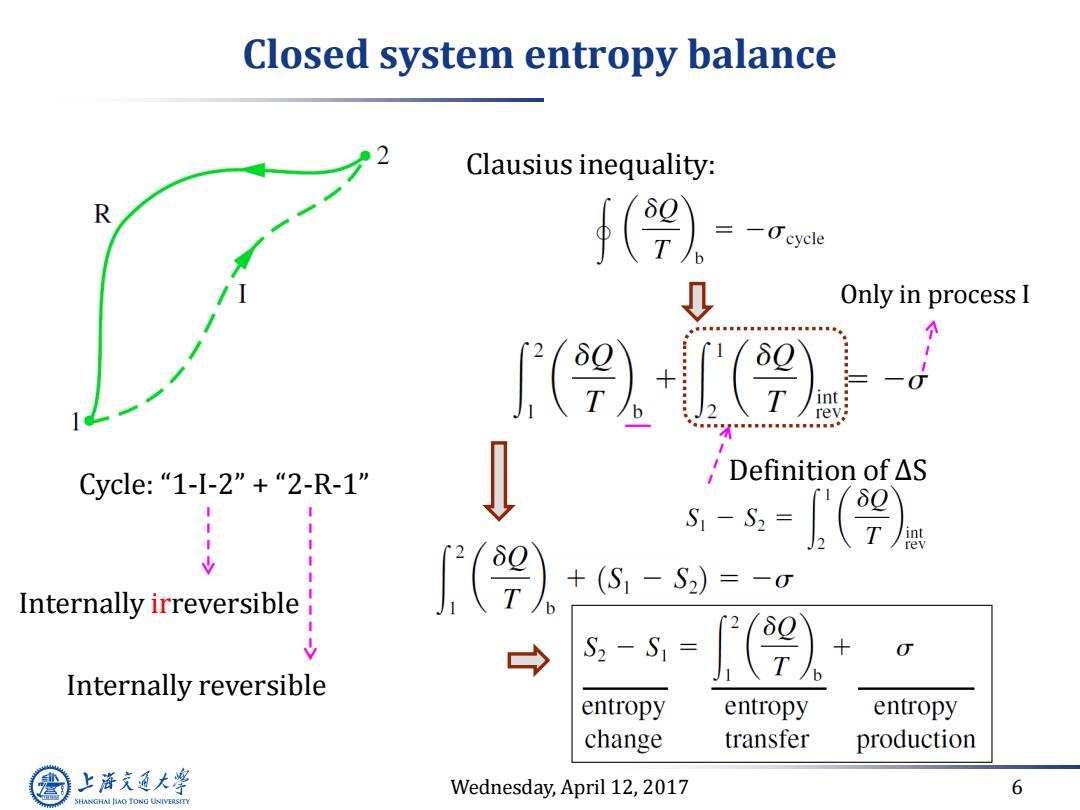
Closed system entropy balance Clausius inequality: R 4(9 eycle 、 Only in process I 个 (9 int rev; Cycle:“1-I-2”+“2-R-1" 'Definition of△S s-=(9) Internally irreversible (9) +(S1-S2)=-0 S2-S1= Internally reversible entropy entropy entropy change transfer production 上游充通大 Wednesday,April 12,2017 6 SHANGHAI JLAO TONG UNIVERSITY
Wednesday, April 12, 2017 6 Closed system entropy balance Cycle: “1-I-2” + “2-R-1” Internally irreversible Internally reversible Clausius inequality: Only in process I Definition of ∆S
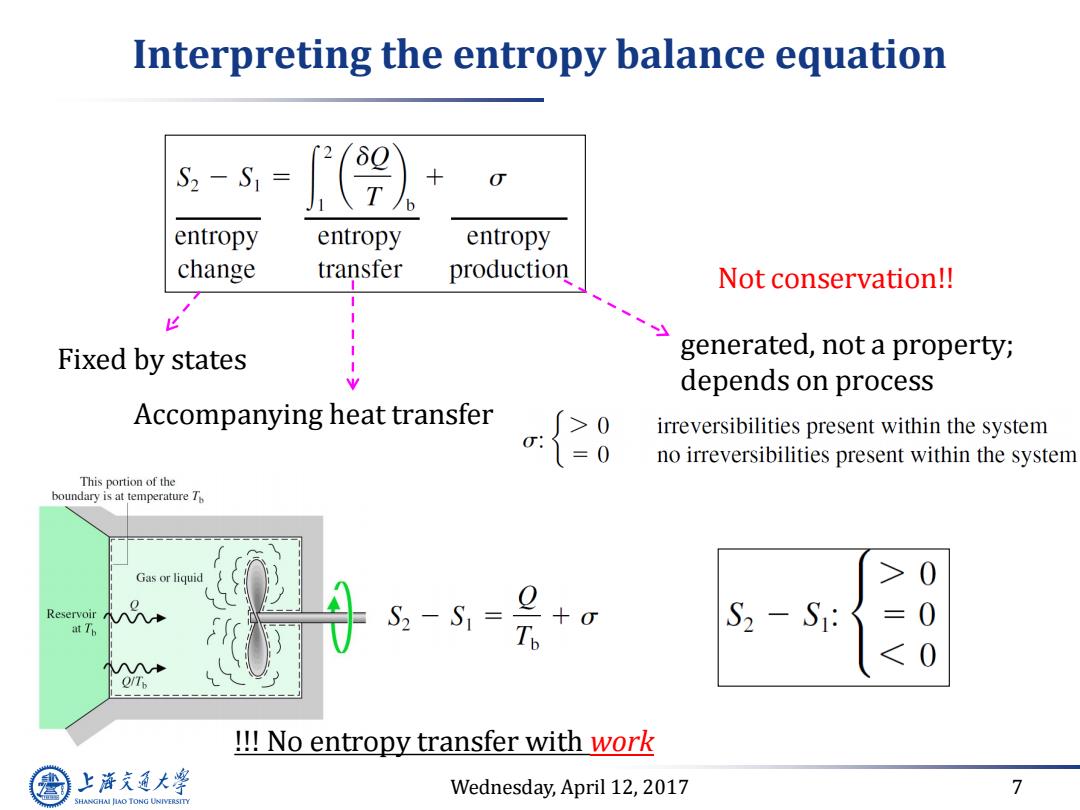
Interpreting the entropy balance equation S2-S1= entropy entropy entropy change transfer production Not conservation!! Fixed by states generated,not a property; depends on process Accompanying heat transfer -{20 irreversibilities present within the system no irreversibilities present within the system This portion of the boundary is at temperature T Gas or liquid 0 Reservoir at Th S:-S=2+o 0 !!No entropy transfer with work 上降文通大学 Wednesday,April 12,2017 7 SHANGHAI JIAO TONG UNIVERSITY
Wednesday, April 12, 2017 7 Interpreting the entropy balance equation Fixed by states Accompanying heat transfer generated, not a property; depends on process !!! No entropy transfer with work Not conservation!!

Other forms of entropy balance Heat transfer at several locations on the boundary 0 T>Constant boundary temperat +0 Time rate basis ds Q +G (closed system entropy rate balance) dt T ©Differential form Non-property 个 上游气通大粤 Wednesday,April 12,2017 8 SHANGHAI JLAO TONG UNIVERSITY
Wednesday, April 12, 2017 8 Other forms of entropy balance Heat transfer at several locations on the boundary Time rate basis Differential form (closed system entropy rate balance) Non-property Constant boundary temperature only

Example 32.2 irreversible process of water Known:water,initially sat.liq.100C;irreversible process; no heat transfer with the surroundings;by paddle wheel. final sat.vap. Find:Wnet/m;o moves freely T System Water boundary 100C Area is not work 100°C Area is not heat 上降文通大学 Wednesday,April 12,2017 9 SHANGHAI JIAO TONG UNIVERSITY
Wednesday, April 12, 2017 9 Example 32.2 irreversible process of water Known: water, initially sat. liq. 100˚C; irreversible process; no heat transfer with the surroundings; by paddle wheel. final sat. vap. Find: Wnet/m; σ moves freely

Solution T Energy balance: 0 100C AU+△KE+APE=E-W Area is not work 100°C Area is not heat Net work on a unit mass basis: U W =-(g-4) m kJ -2087.56 kg (Tab.A-4at100°C Entropy balance: !!Compared with example 32.1 Same state 1 2,but different o kJ 6.048 m =Sg -Sr= kg·K (Tab.A-2 at 100C) 上游充通大 Wednesday,April 12,2017 10 SHANGHAI JIAO TONG UNIVERSITY
Wednesday, April 12, 2017 10 Solution Energy balance: Net work on a unit mass basis: (Tab. A-4 at 100˚C) Entropy balance: (Tab. A-2 at 100˚C) !!! Compared with example 32.1 Same state 1 & 2, but different σ