
研究实验2报告示范一一单入单出BP人工神经网络及算法 研究 一.研究问题描述: 用BP方法实现一个单输入单输出的函数的逼近。假设转换函数的输出范围 在0到1之间。函数取以下3个: f(x)=e,0.2≤x≤0.8 f(x)=0.5+0.3*sinx,0≤x≤1 f(x)=0.5+0.3*sin(2*x),0≤x≤1 二,网络结构: 1.三层前向神经网络 根据逼近定理知,只含一个隐层的前向网络(即三层前向神经网络)是 个通用的逼近器,可以任意逼近函数,因此,在本题中选用三层前向神经网络, 即输入层(x0,y0),一个隐层(x1,y1),输出层(x2,y2)。 2.网络结构 由于要逼近的函数为单输入单输出函数,故输出层只有一个节点;输入层 除了一个样本输入点外,还有一个阈值单元,因此可以看作是两个输入节点:隐 层的节点个数p可以在程序运行时进行选择,以适应和测试不同的逼近效果。由 输入层至隐层的权矩阵记为W0,由隐层到输出层的权矩阵记为W1。 整个网络的结构初步设计如下图所示:(略) 三,算法实现 本实验用C++程序实现该算法。报告中所给出的实验数据均是运行C+程 序所得的结果,然后将这些结果在matlab中画出对应图形。 1.标准BP算法(无动量项): 根据公式:(a为学习率) w(k+1)=w()-a-E1a(k) =w()-a∑(k)k
研究实验 2 报告示范——单入单出 BP 人工神经网络及算法 研究 一.研究问题描述: 用 BP 方法实现一个单输入单输出的函数的逼近。假设转换函数的输出范围 在 0 到 1 之间。函数取以下 3 个: ( ) ,0.2 0.8 x f x e x − = f x x x ( ) 0.5 0.3*sin ,0 1 = + f x x x ( ) 0.5 0.3*sin(2* ),0 1 = + 二.网络结构: 1.三层前向神经网络 根据逼近定理知,只含一个隐层的前向网络(即三层前向神经网络)是一 个通用的逼近器,可以任意逼近函数 f,因此,在本题中选用三层前向神经网络, 即输入层(x0,y0),一个隐层(x1,y1),输出层(x2,y2)。 2.网络结构 由于要逼近的函数为单输入单输出函数,故输出层只有一个节点;输入层 除了一个样本输入点外,还有一个阈值单元,因此可以看作是两个输入节点;隐 层的节点个数 p 可以在程序运行时进行选择,以适应和测试不同的逼近效果。由 输入层至隐层的权矩阵记为 W0,由隐层到输出层的权矩阵记为 W1。 整个网络的结构初步设计如下图所示:(略) 三.算法实现 本实验用 C++程序实现该算法。报告中所给出的实验数据均是运行 C++程 序所得的结果,然后将这些结果在 matlab 中画出对应图形。 1.标准 BP 算法(无动量项): 根据公式:( 为学习率) = − − − − − = − + = − P p l p i l p j l l i j l l i j l l i j l l i j w k k y k w k w k E w k 1 1 , , 1, , 1, , 1, , 1, , ( ) ( ) ( ) ( 1) ( ) / ( )

Lp.(K)-t.fx (k] 1=M-1 6()= f'[xk∑δg(k)-wk)1=M-2l 编写程序,程序执行时允许选择:样本个数p,隐层节点个数midnumber, 学习速率step,训练过程结束条件(即训练结束时允许的最大误差)enderr。 2.加动量项的BP算法 基本原理同上,仅在标准BP算法的基础上,对权矩阵的修改添加动量项, 程序执行时允许选择:样本个数p,隐层节点个数midnumber,学习速率step, 训练过程结束条件(即训练结束时允许的最大误差)enderr,以及动量因子moti。 四.训练结果: 对不同的函数逼近进行训练得到不同的训练结果,下面分别进行讨论: 1.f(x)=e-,0.2≤x≤0.8 (1.)样本个数取为10,隐层节点数取为10,步长0.4,终止误差设为0.001,无 动量项运行结果如下: 训练次数:1850 最终误差:0.000999849 权值矩阵为: -0.601838-1.30367 -1.23252 -0.601838 -2.00658 1.01428 -0.601838 -2.00658 1.01428 -0.601838-2.00658 1.01428 -0.601838-2.00658 1.01428 W0= W1= -0.601838 -2.00658 1.01428 -0.601838-2.00658 1.01428 -0.601838-2.00658 1.01428 -0.601838-2.00658 1.01428 -0.601838-2.00658 1.01428 (这里的权矩阵的取值比较整齐,分析其原因是因为在初始化权矩阵的时候,并
编写程序,程序执行时允许选择:样本个数 p,隐层节点个数 midnumber, 学习速率 step,训练过程结束条件(即训练结束时允许的最大误差)enderr。 2.加动量项的 BP 算法 基本原理同上,仅在标准 BP 算法的基础上,对权矩阵的修改添加动量项, 程序执行时允许选择:样本个数 p,隐层节点个数 midnumber,学习速率 step, 训练过程结束条件(即训练结束时允许的最大误差)enderr,以及动量因子 moti。 四.训练结果: 对不同的函数逼近进行训练得到不同的训练结果,下面分别进行讨论: 1. ( ) ,0.2 0.8 x f x e x − = (1.)样本个数取为10,隐层节点数取为10,步长0.4,终止误差设为0.001,无 动量项运行结果如下: 训练次数:1850 最终误差:0.000999849 权值矩阵为: 0.601838 1.30367 0.601838 2.00658 0.601838 2.00658 0.601838 2.00658 0.601838 2.00658 0 0.601838 2.00658 0.601838 2.00658 0.601838 2.00658 0.601838 2.00658 0.601838 2.00658 W − − − − − − − − − − = − − − − − − − − − − 1.23252 1.01428 1.01428 1.01428 1.01428 1 1.01428 1.01428 1.01428 1.01428 1.01428 W − = (这里的权矩阵的取值比较整齐,分析其原因是因为在初始化权矩阵的时候,并 = − − = − = + = + + '[ ( )] ( ) ( ) 2,...,1 [ ( ) ] '[ ( )] 1 ( ) 1 1 , 1 , 1 , , , , , , f x k k w k l M y k t f x k l M k Nl n l l j n l p n l p j l p j p j l p j l p j
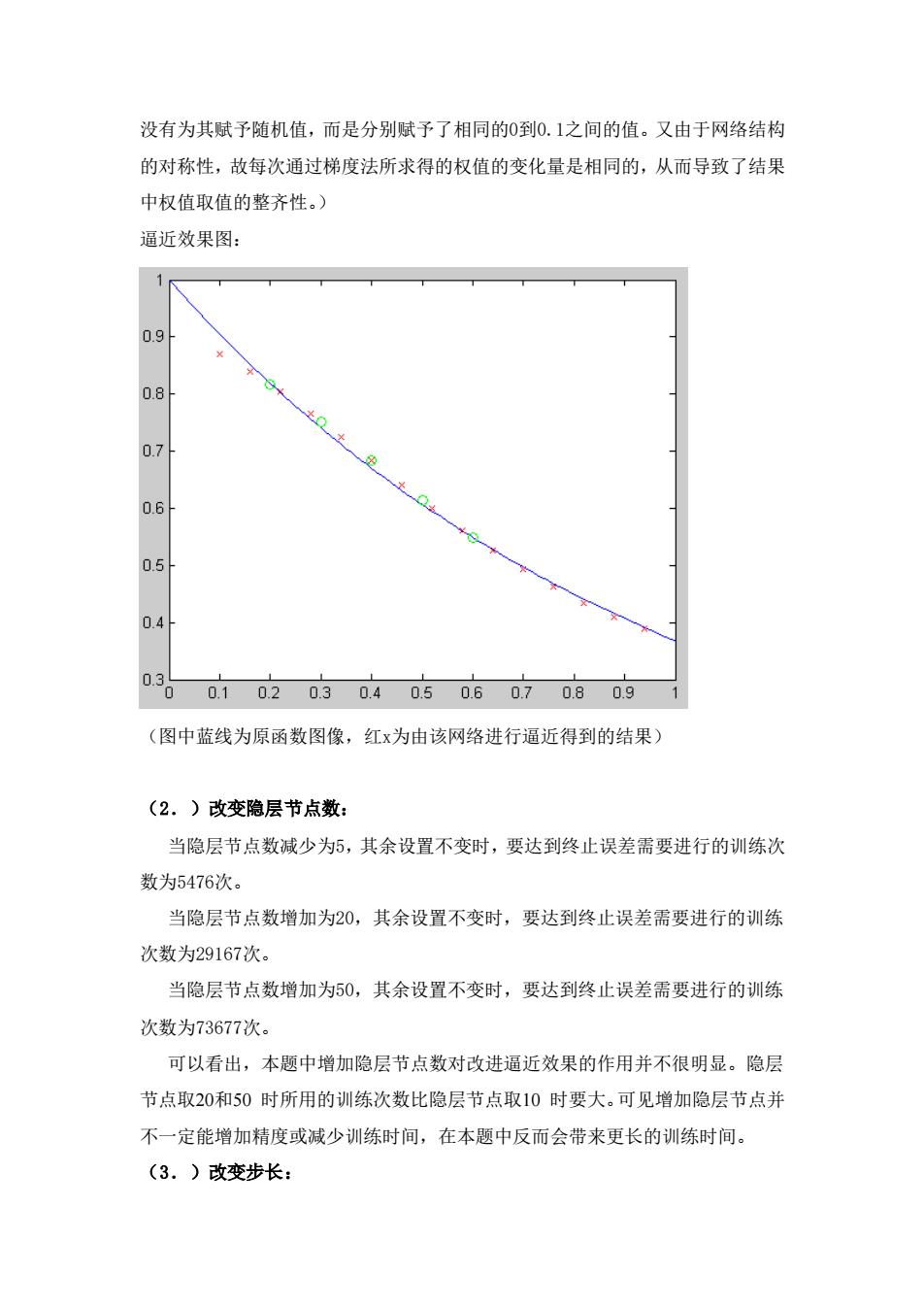
没有为其赋予随机值,而是分别赋予了相同的0到0.1之间的值。又由于网络结构 的对称性,故每次通过梯度法所求得的权值的变化量是相同的,从而导致了结果 中权值取值的整齐性。) 逼近效果图: 0.9 0.8 0.7 0.6 0.5 0.4 0. 0 0.10.20.30.40.50.60.70.80.9 (图中蓝线为原函数图像,红x为由该网络进行逼近得到的结果) (2.)改变隐层节点数: 当隐层节点数减少为5,其余设置不变时,要达到终止误差需要进行的训练次 数为5476次。 当隐层节点数增加为20,其余设置不变时,要达到终止误差需要进行的训练 次数为29167次。 当隐层节点数增加为50,其余设置不变时,要达到终止误差需要进行的训练 次数为73677次。 可以看出,本题中增加隐层节点数对改进逼近效果的作用并不很明显。隐层 节点取20和50时所用的训练次数比隐层节点取10时要大。可见增加隐层节点并 不一定能增加精度或减少训练时间,在本题中反而会带来更长的训练时间。 (3.)改变步长:
没有为其赋予随机值,而是分别赋予了相同的0到0.1之间的值。又由于网络结构 的对称性,故每次通过梯度法所求得的权值的变化量是相同的,从而导致了结果 中权值取值的整齐性。) 逼近效果图: (图中蓝线为原函数图像,红x为由该网络进行逼近得到的结果) (2.)改变隐层节点数: 当隐层节点数减少为5,其余设置不变时,要达到终止误差需要进行的训练次 数为5476次。 当隐层节点数增加为20,其余设置不变时,要达到终止误差需要进行的训练 次数为29167次。 当隐层节点数增加为50,其余设置不变时,要达到终止误差需要进行的训练 次数为73677次。 可以看出,本题中增加隐层节点数对改进逼近效果的作用并不很明显。隐层 节点取20和50 时所用的训练次数比隐层节点取10 时要大。可见增加隐层节点并 不一定能增加精度或减少训练时间,在本题中反而会带来更长的训练时间。 (3.)改变步长:

当步长减小为0.2,其余设置不变时,要达到终止误差需要进行的训练次数 为18993次,明显多于步长为0.4的情形。 当步长增加为0.5,其余设置不变时,要达到终止误差需要进行的训练次数 为7590次,少于步长为0.4的情形。 当步长增加为0.8,其余设置不变时,要达到终止误差需要进行的训练次数 为4449次,明显少于步长为0.4的情形。 而当步长增加为1,其余设置不变时,要达到终止误差需要进行的训练次数 只有3292次。 这说明随着步长的增加,训练的次数可能减小,分析其原因是由于步长增加 意味着权值每次的变化量更大,因此会使收敛更快。但步长增加另一方面可能会 导致振荡,也就是当步长取的较大时,有可能使得权值在误差曲面的极小点两边 来回变化而不能达到极小点。在对其它函数逼近的实验中(实验3),可以看出 该现象。 (4.)增加动量项 当增加动量项,动量因子设为0.2,其余设置不变时,要达到终止误差需要 进行的训练次数为7590次,明显少于相同条件下不加动量项时所用的训练次数。 说明增加动量项加快了收敛。而增加动量项后的训练结果与不加动量项时的结果 几乎完全一样(一般仅在小数点后第五位有点差别),这说明在本例中增加动量 项虽然加快了收敛,但对逼近的程度并无什么改进。 (5.)推广测试 均匀选取5个点进行推广测试,其误差为0.000170499,上图中绿色o形标志 为推广测试的结果,由图及误差可以看出,在本例中的推广测试效果比较好。 2.f(x)=0.5+0.3*sinx,0≤x≤1 (1.)样本个数取为15,隐层节点数取为10,步长0.3,终止误差设为0.001,无 动量项运行结果如下: 训练次数:1485 最终误差:0.000996835 权值矩阵为:
当步长减小为0.2,其余设置不变时,要达到终止误差需要进行的训练次数 为18993次,明显多于步长为0.4的情形。 当步长增加为0.5,其余设置不变时,要达到终止误差需要进行的训练次数 为7590次,少于步长为0.4的情形。 当步长增加为0.8,其余设置不变时,要达到终止误差需要进行的训练次数 为4449次,明显少于步长为0.4的情形。 而当步长增加为1,其余设置不变时,要达到终止误差需要进行的训练次数 只有3292次。 这说明随着步长的增加,训练的次数可能减小,分析其原因是由于步长增加 意味着权值每次的变化量更大,因此会使收敛更快。但步长增加另一方面可能会 导致振荡,也就是当步长取的较大时,有可能使得权值在误差曲面的极小点两边 来回变化而不能达到极小点。在对其它函数逼近的实验中(实验3),可以看出 该现象。 (4.)增加动量项 当增加动量项,动量因子设为0.2,其余设置不变时,要达到终止误差需要 进行的训练次数为7590次,明显少于相同条件下不加动量项时所用的训练次数。 说明增加动量项加快了收敛。而增加动量项后的训练结果与不加动量项时的结果 几乎完全一样(一般仅在小数点后第五位有点差别),这说明在本例中增加动量 项虽然加快了收敛,但对逼近的程度并无什么改进。 (5.)推广测试 均匀选取5个点进行推广测试,其误差为0.000170499,上图中绿色o形标志 为推广测试的结果,由图及误差可以看出,在本例中的推广测试效果比较好。 2. f x x x ( ) 0.5 0.3*sin ,0 1 = + (1.)样本个数取为15,隐层节点数取为10,步长0.3,终止误差设为0.001,无 动量项运行结果如下: 训练次数:1485 最终误差:0.000996835 权值矩阵为:

-0.140785 -1.30367 -1.98133 -0.140785 0.850544 0.450068 -0.140785 0.850544 0.450068 -0.140785 0.850544 0.450068 -0.140785 0.850544 0.450068 W0= W1= -0.140785 0.850544 0.450068 -0.1407850.850544 0.450068 -0.140785 0.850544 0.450068 -0.140785 0.850544 0.450068 -0.140785 0.850544 0.450068 (这里的权矩阵的取值比较整齐,原因同上。) 逼近效果图: 0.85 0.8 0.75 0.7 0.65 0.61 0.55 0.5 0.1 0.2 0.30.40.50.607 0.80.9 (图中蓝线为原函数图像,红x为由该网络进行逼近得到的结果) (2.)改变隐层节点数: 当隐层节点数减少为5,其余设置不变时,要达到终止误差需要进行的训练次 数为1215次。 当隐层节点数增加为20,其余设置不变时,要达到终止误差需要进行的训练 次数为1927次
0.140785 1.30367 0.140785 0.850544 0.140785 0.850544 0.140785 0.850544 0.140785 0.850544 0 0.140785 0.850544 0.140785 0.850544 0.140785 0.850544 0.140785 0.850544 0.140785 0.850544 W − − − − − − = − − − − − 1.98133 0.450068 0.450068 0.450068 0.450068 1 0.450068 0.450068 0.450068 0.450068 0.450068 W − = (这里的权矩阵的取值比较整齐,原因同上。) 逼近效果图: (图中蓝线为原函数图像,红x为由该网络进行逼近得到的结果) (2.)改变隐层节点数: 当隐层节点数减少为5,其余设置不变时,要达到终止误差需要进行的训练次 数为1215次。 当隐层节点数增加为20,其余设置不变时,要达到终止误差需要进行的训练 次数为1927次

当隐层节点数增加为50,其余设置不变时,要达到终止误差需要进行的训练 次数为3002次。 可以看出,本题中增加隐层节点数对改进逼近效果的作用并不很明显。 (3.)改变步长: 当步长减小为0.2,其余设置不变时,要达到终止误差需要进行的训练次数 为4365次,明显多于步长为0.4的情形。 当步长增加为0.5,其余设置不变时,要达到终止误差需要进行的训练次数 为1748次,少于步长为0.4的情形。 当步长增加为0.8,其余设置不变时,要达到终止误差需要进行的训练次数 为1542次,明显少于步长为0.4的情形。 而当步长增加为1,其余设置不变时,要达到终止误差需要进行的训练次数 只有1404次。 这说明在本题中随着步长的增加,训练的次数减少。 (4.)增加动量项 当增加动量项,动量因子设为0.2,其余设置不变时,要达到终止误差需要 进行的训练次数为893次,明显少于相同条件下不加动量项时所用的训练次数。 说明增加动量项加快了收敛。同时,在matlab中标出增加动量项后的训练结果(红 色0标记),可以看出其与不加动量项时的结果几乎完全一样,这说明在本例中 增加动量项虽然加快了收敛,但对逼近的程度并无明显改进。 (5.)推广测试 均匀选取5个点进行推广测试,其误差为0.000186291,上图中绿色o形标志 为推广测试的结果,由图及误差可以看出,在本例中的推广测试效果可以接受。 3.f(x)=0.5+0.3*sin(2*x),0≤x≤1 (1.)样本个数取为15,隐层节点数取为10,步长0.3,终止误差设为0.001,无 动量项运行结果如下: 训练次数:34044 最终误差:0.000999987 权值矩阵为:
当隐层节点数增加为50,其余设置不变时,要达到终止误差需要进行的训练 次数为3002次。 可以看出,本题中增加隐层节点数对改进逼近效果的作用并不很明显。 (3.)改变步长: 当步长减小为0.2,其余设置不变时,要达到终止误差需要进行的训练次数 为4365次,明显多于步长为0.4的情形。 当步长增加为0.5,其余设置不变时,要达到终止误差需要进行的训练次数 为1748次,少于步长为0.4的情形。 当步长增加为0.8,其余设置不变时,要达到终止误差需要进行的训练次数 为1542次,明显少于步长为0.4的情形。 而当步长增加为1,其余设置不变时,要达到终止误差需要进行的训练次数 只有1404次。 这说明在本题中随着步长的增加,训练的次数减少。 (4.)增加动量项 当增加动量项,动量因子设为0.2,其余设置不变时,要达到终止误差需要 进行的训练次数为893次,明显少于相同条件下不加动量项时所用的训练次数。 说明增加动量项加快了收敛。同时,在matlab中标出增加动量项后的训练结果(红 色o标记),可以看出其与不加动量项时的结果几乎完全一样,这说明在本例中 增加动量项虽然加快了收敛,但对逼近的程度并无明显改进。 (5.)推广测试 均匀选取5个点进行推广测试,其误差为0.000186291,上图中绿色o形标志 为推广测试的结果,由图及误差可以看出,在本例中的推广测试效果可以接受。 3. f x x x ( ) 0.5 0.3*sin(2* ),0 1 = + (1.)样本个数取为15,隐层节点数取为10,步长0.3,终止误差设为0.001,无 动量项运行结果如下: 训练次数:34044 最终误差:0.000999987 权值矩阵为:
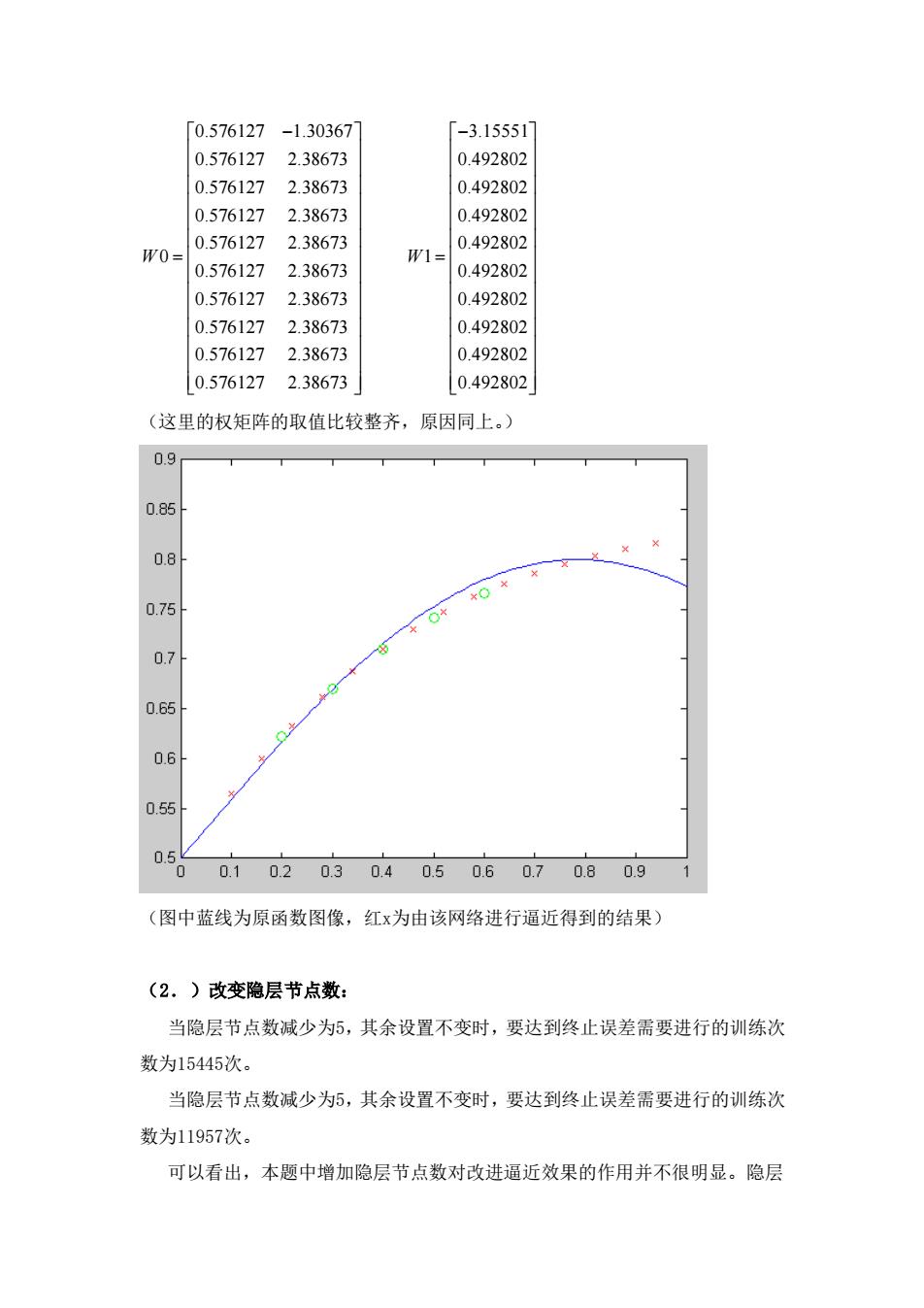
「0.576127 -1.30367 -3.155517 0.576127 2.38673 0.492802 0.576127 2.38673 0.492802 0.576127 2.38673 0.492802 0.576127 2.38673 0.492802 W0= W1= 0.576127 2.38673 0.492802 0.576127 2.38673 0.492802 0.576127 2.38673 0.492802 0.576127 2.38673 0.492802 0.576127 2.38673 0.492802 (这里的权矩阵的取值比较整齐,原因同上。) 0.9 0.85 0.8 0.75 0.7 0.65 0.6 0.55 0. 0 0.1 0.2 0.30.4 0.50.60.7 0.8 0.9 (图中蓝线为原函数图像,红x为由该网络进行逼近得到的结果) (2.)改变隐层节点数: 当隐层节点数减少为5,其余设置不变时,要达到终止误差需要进行的训练次 数为15445次。 当隐层节点数减少为5,其余设置不变时,要达到终止误差需要进行的训练次 数为11957次。 可以看出,本题中增加隐层节点数对改进逼近效果的作用并不很明显。隐层
0.576127 1.30367 0.576127 2.38673 0.576127 2.38673 0.576127 2.38673 0.576127 2.38673 0 0.576127 2.38673 0.576127 2.38673 0.576127 2.38673 0.576127 2.38673 0.576127 2.38673 W − = 3.15551 0.492802 0.492802 0.492802 0.492802 1 0.492802 0.492802 0.492802 0.492802 0.492802 W − = (这里的权矩阵的取值比较整齐,原因同上。) (图中蓝线为原函数图像,红x为由该网络进行逼近得到的结果) (2.)改变隐层节点数: 当隐层节点数减少为5,其余设置不变时,要达到终止误差需要进行的训练次 数为15445次。 当隐层节点数减少为5,其余设置不变时,要达到终止误差需要进行的训练次 数为11957次。 可以看出,本题中增加隐层节点数对改进逼近效果的作用并不很明显。隐层

节点取20和50时所用的训练次数比隐层节点取10时要大。增加隐层节点并不一 定能增加精度或减少训练时间,在本题中反而会带来更长的训练时间。 (3.)改变步长: 当步长减小为0.2,其余设置不变时,要达到终止误差需要进行的训练次数 为51064次,明显多于步长为0.4的情形。 当步长增加为0.5,其余设置不变时,要达到终止误差需要进行的训练次数 为118280次,少于步长为0.4的情形。 当步长增加为0.8,其余设置不变时,训练速度极慢,训练的误差出现明显 的振荡,例如:在某一步误差为0.0066后,其下一步误差又增加为0.0092,而接 下来一步的误差又变为0.0065…,该例子说明了步长较大时,若取得合适则会 加快收敛,若不合适,则会造成振荡而不再收敛。 (4.)增加动量项 当增加动量项,动量因子设为0.2,其余设置不变时,要达到终止误差需要 进行的训练次数为20467次,少于相同条件下不加动量项时所用的训练次数。说 明增加动量项加快了收敛。 五.实验总结 (1.)网络结构: 本实验选用三层前向神经网络使用BP算法以及加动量项的BP算法实现对单 输入单输出函数的逼近,通过对三个不同函数的逼近实验测试了BP算法的性能 及隐层节点数目、步长、动量项等因素对BP网络训练和测试的影响。 其中,适当增加隐层节点数可以改善网络性能,但在本实验中,隐层节点数 取20和50时所用的训练次数比隐层节点取10时要大。可见增加隐层节点并不一 定能增加精度或减少训练时间,在本实验中反而会带来更长的训练时间:训练次 数随着步长的增加而减小,但不合适的步长增加会引起振荡而增加训练次数甚至 不再收敛:增加动量项后在相同条件下网络的收敛速度明显快于不加动量项时的 速度,不过从本实验看来增加动量项对逼近的精度改善并不明显:对在0.2到0.6 区间内均匀取值的数据进行测试,推广性较好,但并不是太理想。 由此可见,BP算法虽然理论上可以实现任意函数的逼近,但网络结构的具体
节点取20和50 时所用的训练次数比隐层节点取10 时要大。增加隐层节点并不一 定能增加精度或减少训练时间,在本题中反而会带来更长的训练时间。 (3.)改变步长: 当步长减小为0.2,其余设置不变时,要达到终止误差需要进行的训练次数 为51064次,明显多于步长为0.4的情形。 当步长增加为0.5,其余设置不变时,要达到终止误差需要进行的训练次数 为118280次,少于步长为0.4的情形。 当步长增加为0.8,其余设置不变时,训练速度极慢,训练的误差出现明显 的振荡,例如:在某一步误差为0.0066后,其下一步误差又增加为0.0092,而接 下来一步的误差又变为0.0065……,该例子说明了步长较大时,若取得合适则会 加快收敛,若不合适,则会造成振荡而不再收敛。 (4.)增加动量项 当增加动量项,动量因子设为0.2,其余设置不变时,要达到终止误差需要 进行的训练次数为20467次,少于相同条件下不加动量项时所用的训练次数。说 明增加动量项加快了收敛。 五.实验总结 (1.)网络结构: 本实验选用三层前向神经网络使用BP算法以及加动量项的BP算法实现对单 输入单输出函数的逼近,通过对三个不同函数的逼近实验测试了BP算法的性能 及隐层节点数目、步长、动量项等因素对BP网络训练和测试的影响。 其中,适当增加隐层节点数可以改善网络性能,但在本实验中,隐层节点数 取20和50 时所用的训练次数比隐层节点取10 时要大。可见增加隐层节点并不一 定能增加精度或减少训练时间,在本实验中反而会带来更长的训练时间;训练次 数随着步长的增加而减小,但不合适的步长增加会引起振荡而增加训练次数甚至 不再收敛;增加动量项后在相同条件下网络的收敛速度明显快于不加动量项时的 速度,不过从本实验看来增加动量项对逼近的精度改善并不明显;对在0.2到0.6 区间内均匀取值的数据进行测试,推广性较好,但并不是太理想。 由此可见,BP算法虽然理论上可以实现任意函数的逼近,但网络结构的具体

设计及各种参数的选取并不容易。并且网络的收敛速度及性能比较差,受到初始 权值、样本取值、学习速率等因素的影响,对函数的选择也有一定的要求。因此, 标准的BP算法应结合一些其他的措施(如增加动量项,引入全局优化技术等) 进行改进和优化
设计及各种参数的选取并不容易。并且网络的收敛速度及性能比较差,受到初始 权值、样本取值、学习速率等因素的影响,对函数的选择也有一定的要求。因此, 标准的BP算法应结合一些其他的措施(如增加动量项,引入全局优化技术等) 进行改进和优化