
第八章Hopfield神经网络 Hopfield网络结构和模型 Hopfield网络输出的计算过程(离散) Hopfield网络的稳定性 ■Hopfield网络的学习算法 Hopfield网络的几个问题 Hopfield网络的MATLAB实现示例
Hopfield网络结构和模型 Hopfield网络输出的计算过程(离散) Hopfield网络的稳定性 Hopfield网络的学习算法 Hopfield网络的几个问题 Hopfield网络的MATLAB实现示例 第八章 Hopfield神经网络

概述 Hopfield网络是神经网络发展历史上的一个重要的里 程碑。由美国加州理工学院物理学家J.J.Hopfield教授于 1982年提出,是一种单层反馈神经网络。 Hopfield网络: 生元件构成的反馈系统,其 稳定状态的分村 ]络要享乐得条.'9旆 Hopfield设计 莫型的电路,并地解决 了旅行商(TSP) 问题 Hopfield网 续型两种网络模型,分 别记作DHNN pfield Neural Network) CHNN (Continues Hopfield Neural Network)
概述 Hopfield网络是神经网络发展历史上的一个重要的里 程碑。由美国加州理工学院物理学家J.J.Hopfield教授于 1982年提出,是一种单层反馈神经网络。 Hopfield网络是一种由非线性元件构成的反馈系统,其 稳定状态的分析比前向神经网络要复杂得多。1984年, Hopfield设计并研制了网络模型的电路,并成功地解决 了旅行商(TSP)计算难题(优化问题)。 Hopfield网络分为离散型和连续型两种网络模型,分 别记作DHNN (Discrete Hopfield Neural Network) 和CHNN (Continues Hopfield Neural Network) 。 Hello,I’m John Hopfield

8-1 Hopfield网络结构和模型 Hopfield网络有离散与连续两种类型。 Hopfield网络是得到最充分研究和应用的神经 网络模型之一,在众多的研究者之中,美国科学家 J.J Hopfield的工作具有特别重要的意义,他为这 一网络引入了一种稳定过程,即提出了人工神经网 络能量函数(也称李雅普诺夫函数)的概念,使网 络的运行稳定性判断有了可靠而简便的依据。 Hopfield网络在联想存取及优化计算等领域得 到了成功的应用,拓宽了神经网络的应用范围
8-1 Hopfield网络结构和模型 Hopfield网络有离散与连续两种类型。 Hopfield网络是得到最充分研究和应用的神经 网络模型之一,在众多的研究者之中,美国科学家 J.J Hopfield的工作具有特别重要的意义,他为这 一网络引入了一种稳定过程,即提出了人工神经网 络能量函数(也称李雅普诺夫函数)的概念,使网 络的运行稳定性判断有了可靠而简便的依据。 Hopfield网络在联想存取及优化计算等领域得 到了成功的应用,拓宽了神经网络的应用范围

8-1-1离散型Hopfield网络 离散Hopfield网结构见图(a),是单层反馈非线性网,每 节点的输出反馈至输入。 Hopfield用模拟电路(电阻、电容和运算放大器)实现网 络的神经元(节点),见图(b)。 -I (a)结构示意图 (b) 图9-1离散型opfeld网络
8-1-1 离散型Hopfield网络 离散Hopfield网结构见图(a),是单层反馈非线性网,每 一节点的输出反馈至输入。 Hopfield用模拟电路(电阻、电容和运算放大器)实现网 络的神经元(节点),见图(b)。 图9-1 离散型Hopfeld网络

8-l-1离散型Hopfield网络 网络为一层结构的反馈网络,能处理双极型离散数据(即输入-1,+1), 及二进制数据(0,1)。 给定初始输入时,网络处于特定的初始状态。网络从初始状态开始运行 可得到网络下一状态的输出。这个输出状态通过反馈连接送到网络的输入 端,作为下一阶段运行的输入信号,它可能与初始输入信号不同。如此下 去,网络的整个运行过程就是上述反馈过程的重复。如果网络稳定,那么 随着多次反馈运行,网络状态最后将达到稳态。用公式表达为: v(0)=x, vt+)=f,(∑W,y,(0-0,) 其中已被定义,为方便起见,常取0值。若有某个时刻t,从此以后网 络状态下不再变迁,即有 v(t+1),则有输出 y=v(t)
网络为一层结构的反馈网络,能处理双极型离散数据(即输入 –1,+1), 及二进制数据(0,1)。 给定初始输入时,网络处于特定的初始状态。网络从初始状态开始运行, 可得到网络下一状态的输出。这个输出状态通过反馈连接送到网络的输入 端,作为下一阶段运行的输入信号,它可能与初始输入信号不同。如此下 去,网络的整个运行过程就是上述反馈过程的重复。如果网络稳定,那么 随着多次反馈运行,网络状态最后将达到稳态。用公式表达为: + = − = = n i j j i j i i j j v t f W v t v x 1 ( 1) ( ( ) ) (0) 其中 已被定义,为方便起见, 常取0值。若有某个时刻t,从此以后网 络状态下不再变迁,即有 ,则有输出 。 j f i v(t +1) = v(t) y = v(t) 8-1-1 离散型Hopfield网络

8-l-1离散型Hopfield网络 ·相关参数说明 任意神经元泻间的突触权值为”,,神经元之间 连接是对称的,神经元自身无连接 每个神经元都同其他的神经元相连,其输出信号经过 其他神经元又有可能反馈给自己 设Hopfield网络中有n个神经元,其中任意神经元的 输入用,表示,输出V,用表示,它们都是时间的函 数,其中y,(t)也称为神经元在时刻的状态。 y,()=∑w,4,)+b y,(t+1)=f(y,(t) j≠i
8-1-1 离散型Hopfield网络 ◼ 相关参数说明 ❑ 任意神经元 与 间的突触权值为 ,神经元之间 连接是对称的,神经元自身无连接. ❑ 每个神经元都同其他的神经元相连,其输出信号经过 其他神经元又有可能反馈给自己 ❑ 设Hopfield网络中有n个神经元,其中任意神经元的 输入用 表示,输出 用表示,它们都是时间的函 数,其中 也称为神经元在时刻 的状态。 n 1 ( ) ( ) i ij j i j j i v t w u t b = = + ( 1) ( ( )) i i v t f v t + = i j wij i u i v ( ) t i v t

8-l-1离散型Hopfield网络 激励函数 立0+4≥0 j≠1 ,(t+1)= 1 0负<0 j
激励函数 n 1 n 1 1 ( ) 0 ( 1) 1 ( ) 0, ij j i j j i i ij j i j j i w v t b v t w v t b = = + + = − + 8-1-1 离散型Hopfield网络

8-1-2连续型Hopfield网络 连续Hopfield网结构见图(a),是单层反馈非线性网 每一节点的输出反馈至输入。 Hopfield用模拟电路(电阻、电容和运算放大器)实现 网络的神经元(节点),见图(b)。 (a)结构示意图 (b) 图9-2连续型Hopfeld网络
8-1-2 连续型Hopfield网络 连续Hopfield网结构见图(a),是单层反馈非线性网, 每一节点的输出反馈至输入。 Hopfield用模拟电路(电阻、电容和运算放大器)实现 网络的神经元(节点),见图(b)。 图9-2 连续型Hopfeld网络 (b) Rij Vj Vi Ci Ri i ui I f (•) f (•)
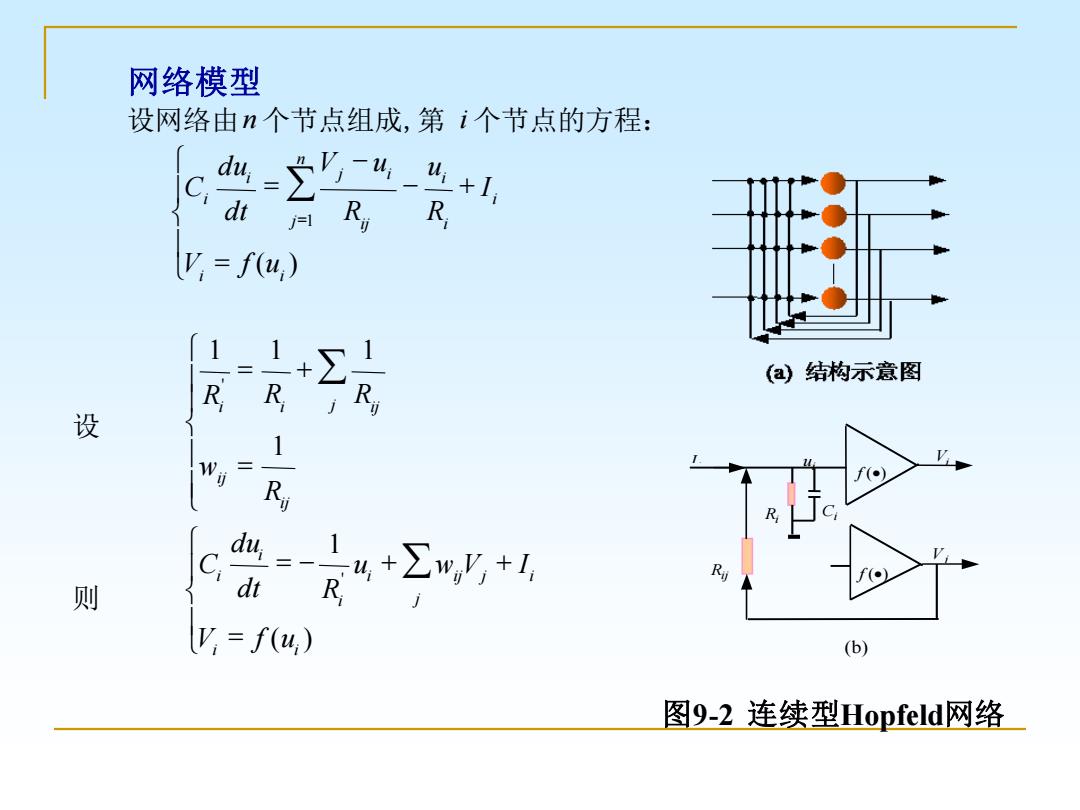
网络模型 设网络由n个节点组成,第i个节点的方程: Ry R j=1 V=f(u,) ()结构示意图 R R R 设 1 R du= 则 C 1 dt 4+∑w,+1 R V,=f(u) (b) 图9-2连续型Hopfeld网络
图9-2 连续型Hopfeld网络 (b) Rij Vj Vi Ci Ri i ui I f (•) f (•) 网络模型 设网络由n 个节点组成,第 i 个节点的方程: = − + − = = ( ) 1 i i n j i i i ij j i i i V f u I R u R V u dt du C 设 1 1 1 1 R R R w R i i j ij ij ij ' = + = 则 C du dt R u w V I V f u i i i i ij j j i i i = − + + = 1 ' ( )
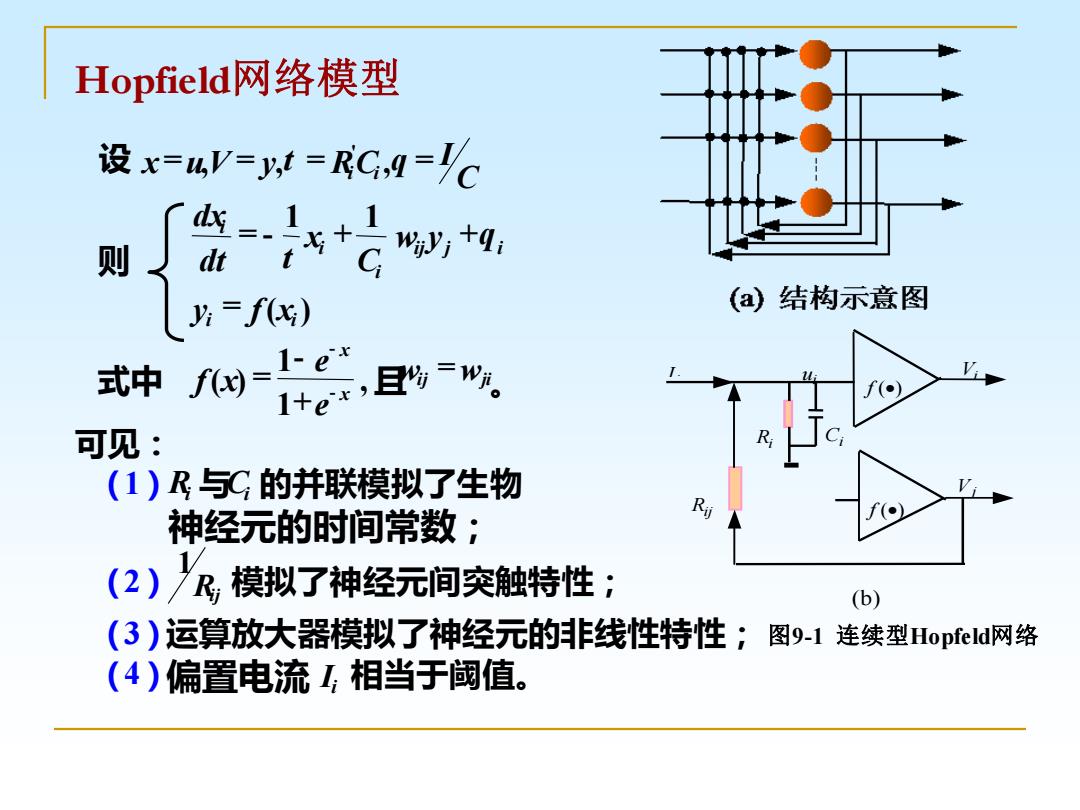
Hopfield网络模型 设x=4V=t=RC,A=C 则 dt 片=fG) (a结构示意图 式中f= 可见: (1)R与C的并联模拟了生物 神经元的时间常数: R (2)£,模拟了神经元间突触特性; (b) (3)运算放大器模拟了神经元的非线性特性;图9-1连续型HopfeldP网络 (4)偏置电流1相当于阈值
Hopfield网络模型 图9-1 连续型Hopfeld网络 (b) Rij Vj Vi Ci Ri i ui I f (•) f (•) 运算放大器模拟了神经元的非线性特性; 设 x uV y RC I i i C = , = , = , = ' t q 则 dx dt x C w y y f x i i i ij j i i i = - + + = 1 1 t q ( ) 式中 f x e e x x ( ) = - + - - 1 1 , 且wij =wji 。 可见: (1)Ri 与Ci 的并联模拟了生物 (2) 1 Rij 模拟了神经元间突触特性; (3) (4)偏置电流 Ii 相当于阈值。 神经元的时间常数;