
第六章 径向基函数神经网络 RBF网络结构和模型 RBF网络输出的计算过程 RBF网络的一个实例 RBF网络的学习算法 RBF网络参数的有教师学习算法 ·RBF网络的几个问题 ·RBF网络的应用示例与MATLAB实现 2006-12-12 北京科技大学付冬梅 2
2006-12-12 北京科技大学 付冬梅 2 •RBF网络结构和模型 •RBF网络输出的计算过程 •RBF网络的一个实例 •RBF网络的学习算法 •RBF网络参数的有教师学习算法 •RBF网络的几个问题 •RBF网络的应用示例与MATLAB实现

6-0概述 ■1985年,Powell:提出了多变量插值的径向基 数(Radical Basis Function,RBF)方法 ■I988年,Moody和Darken提出了一种神经网辂 结构,即RBF神经网辂 RBF网络是一种三层前向网辂 RBF网络的基本思想 用RBF作为隐单元的“基”构成隐含层空间,将输入头量 直接(即不需要通过牧连接)映射到隐空间 当RBF的中心点确定后,映射关系也就确定 口隐含层空间到输出空间的映射是孩性的 2006-12-12 北京科技大学付冬梅
2006-12-12 北京科技大学 付冬梅 3 6-0 概述 n 1985年,Powell提出了多变量插值的径向基函 数(Radical Basis Function,RBF)方法 n 1988年, Moody和Darken提出了一种神经网络 结构,即RBF神经网络 n RBF网络是一种三层前向网络 n RBF网络的基本思想 q 用RBF作为隐单元的“基”构成隐含层空间,将输入矢量 直接(即不需要通过权连接)映射到隐空间 q 当RBF的中心点确定后,映射关系也就确定 q 隐含层空间到输出空间的映射是线性的

6-0概述 ·径向基神经网络的神经元结构 X1 W1h X2 W2h dist Wih Xm ■激活函数采用径向基函数 以输入和权值向量之间的dist距离作为自变量 R(小dist)=edst 2006-12-12 北京科技大学付冬梅
2006-12-12 北京科技大学 付冬梅 4 n 径向基神经网络的神经元结构 n 激活函数采用径向基函数 以输入和权值向量之间的 距离作为自变量 2 - dist R ( dist )=e dist 6-0 概述
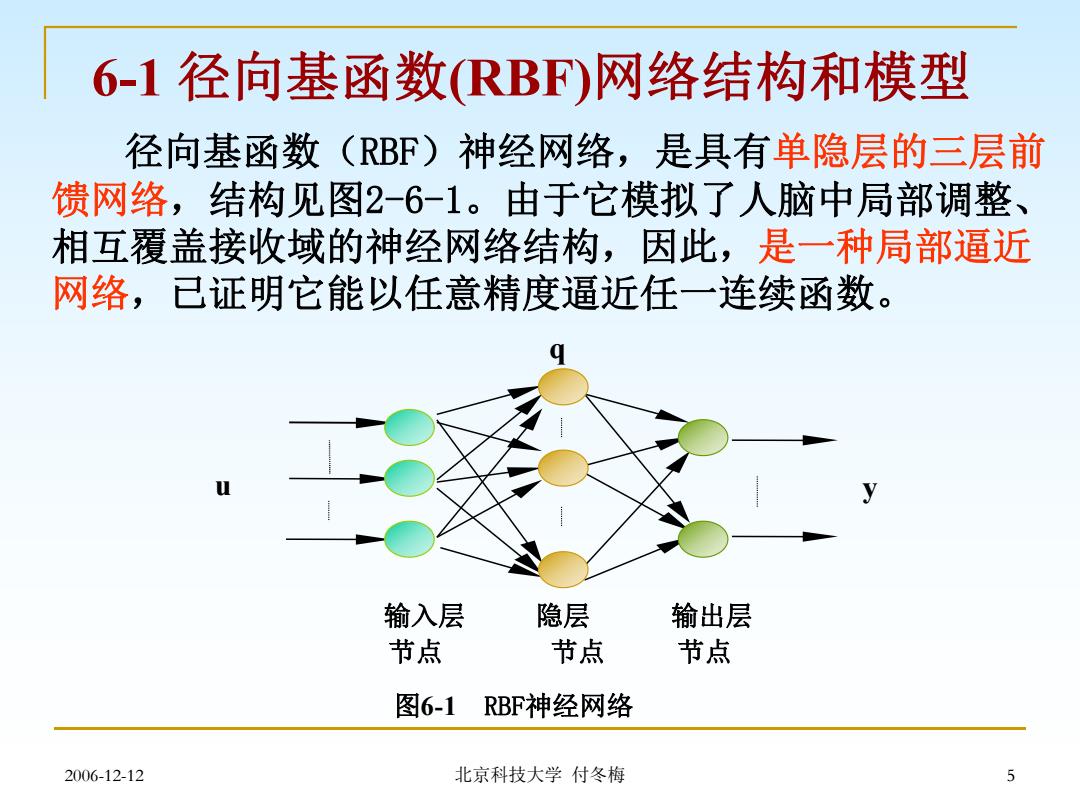
6-1径向基函数RBF)网络结构和模型 径向基函数(RBF)神经网络,是具有单隐层的三层前 馈网络,结构见图2-6-1。由于它模拟了人脑中局部调整、 相互覆盖接收域的神经网络结构,因此,是一种局部逼近 网络,已证明它能以任意精度逼近任一连续函数。 输入层 隐层 输出层 节点 节点 节点 图6-1 RBF神经网络 2006-12-12 北京科技大学付冬梅
2006-12-12 北京科技大学 付冬梅 5 6-1 径向基函数(RBF)网络结构和模型 径向基函数(RBF)神经网络,是具有单隐层的三层前 馈网络,结构见图2-6-1。由于它模拟了人脑中局部调整、 相互覆盖接收域的神经网络结构,因此,是一种局部逼近 网络,已证明它能以任意精度逼近任一连续函数。 输入层 隐层 输出层 节点 节点 节点 图6-1 RBF神经网络 u y q
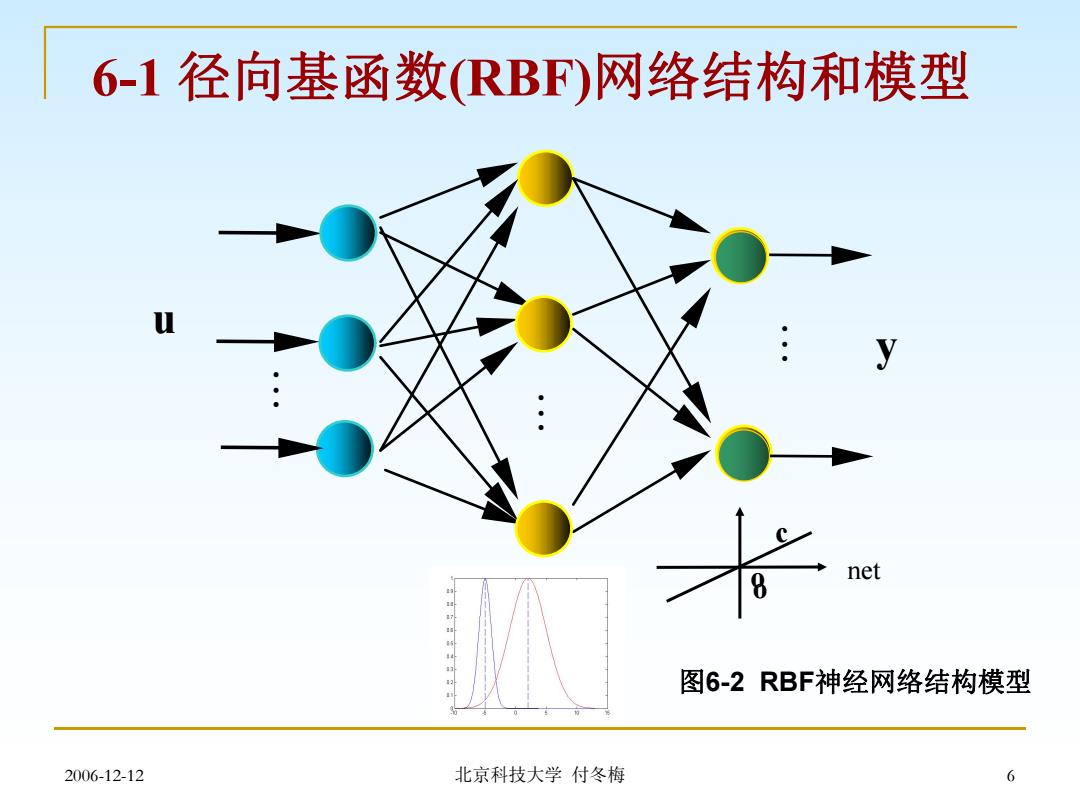
6-1径向基函数RBF)网络结构和模型 y net 图6-2RBF神经网络结构模型 2006-12-12 北京科技大学付冬梅 6
2006-12-12 北京科技大学 付冬梅 6 6-1 径向基函数(RBF)网络结构和模型 u y net o c 图6-2 RBF神经网络结构模型

6-1径向基函数RBF)网络结构和模型 RBF网络的神经元模型是 改进了感知器神经元模型得 到的。 输入层: X w,=1,f(x)=x 隐层: f(x) (net-μ)2 f(net)=e 202 维 n (-4)-4) f(X)=e 20j 二维 图6-3RBF神经元结构模型 输出层:f(x)=kx 2006-12-12 北京科技大学付冬梅
2006-12-12 北京科技大学 付冬梅 7 n j u u u1 y x wn w1 f (x) RBF网络的神经元模型是 改进了感知器神经元模型得 到的。 输入层: 隐层: 输出层: f (x) kx 1, ( ) wij f x x 6-1 径向基函数(RBF)网络结构和模型 2 2 ( ) 2 ( ) net f net e 一维 2 ( ) ( ) 2 ( ) T i i i i j x x f X e 二维 图6-3 RBF神经元结构模型

6-1径向基函数RBF)网络结构和模型 高斯RBF网络隐节点输出: g,=Ru-c)'∑(u-c) [·]:向量u与,的马氏距离。 当Σ,为对角阵、单位阵时分别为 非线性作用函数RBF: R(x)=cxp(-zx) x=(u-c,)'(u-c,) u:n维输入向量; C;:第i个隐节点的中心O,:第i个隐节点的标准化参数; 。):第i个隐节点第j分量的标准化参数。 2006-12-12 北京科技大学付冬梅 8
2006-12-12 北京科技大学 付冬梅 8 高斯 RBF 网络隐节点输出: qi R i T i i u c u c 1 [·]:向量 u 与 ci的马氏距离。 当i 为对角阵、单位阵时分别为 n j ijj j ij i u c q R 1 2 2 , qi R i T i i (u c ) (u c ) 2 非线性作用函数 RBF: ) 2 1 R(x) exp( x , 2 ( ) ( ) i i T i u c u c x u:n 维输入向量; i c :第 i 个隐节点的中心; i :第 i 个隐节点的标准化参数; i j j :第 i 个隐节点第 j 分量的标准化参数。 6-1 径向基函数(RBF)网络结构和模型

6-1径向基函数RBF)网络结构和模型 (1)一维高斯RBF 自变量u、中心c是一维,则有 图(a):w=-l0~15,左高斯RBF:c=-5,o=1; 右高斯RBF:C=2,o=3。 0.9 0.8 0.7 0.6 0.5 0.4 0.3 02 0.1 图6-4RBF网络隐层作用函数 10 15 (a) 2006-12-12 北京科技大学付冬梅 9
2006-12-12 北京科技大学 付冬梅 9 (a) (1) 一维高斯 RBF 自变量 u 、中心c 是一维,则有 2 2 ( ) 2 1 [ ] exp u c R 图 (a):u 10 ~ 15 ,左高斯 RBF:c 5, 1 ; 右高斯 RBF:c 2, 3。 6-1 径向基函数(RBF)网络结构和模型 图6-4 RBF网络隐层作用函数
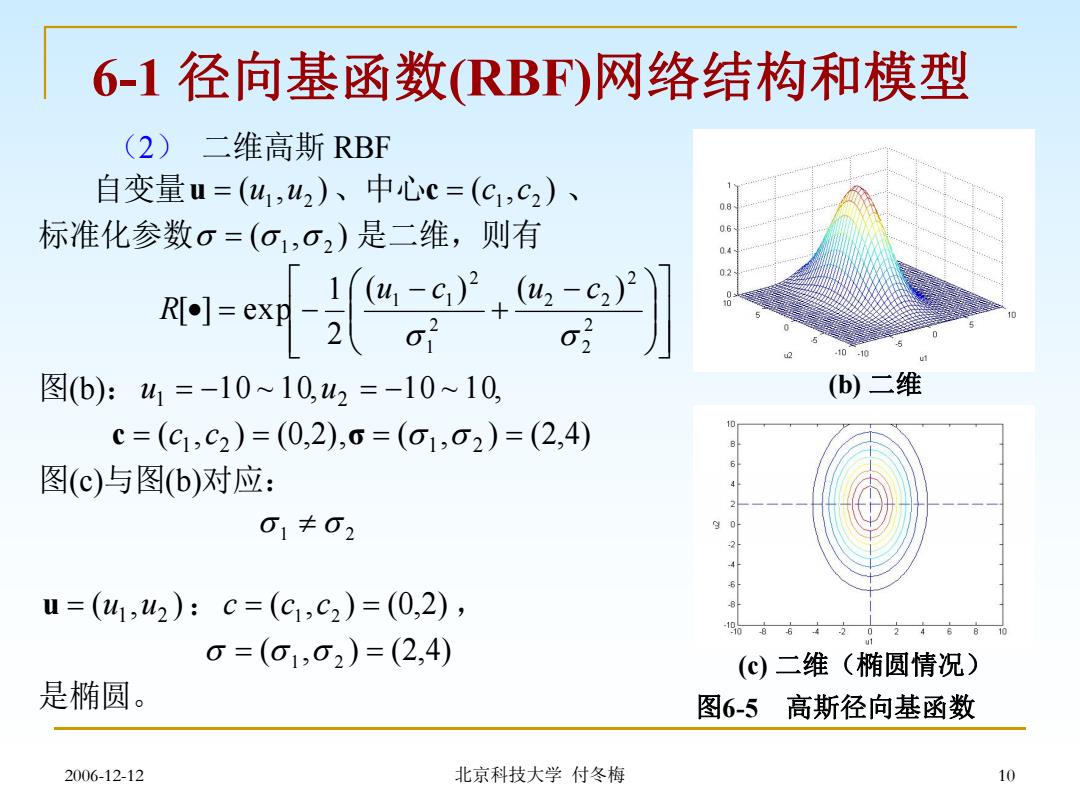
6-1径向基函数RBF)网络结构和模型 (2)二维高斯RBF 自变量u=(41,2)、中心c=(c1,C2)、 标准化参数σ=(o1,02)是二维,则有 02 e, 10-10 图(b):41=-10~10,u2=-10~10, (b)二维 C=(C1,C2)=(0,2),0=(o1,02)=(2,4) 图(c)与图b)对应: 01≠02 u=(u1,42):c=(C1,c2)=(0,2), 0=(01,02)=(2,4) (c)二维(椭圆情况) 是椭圆。 图6-5高斯径向基函数 2006-12-12 北京科技大学付冬梅 10
2006-12-12 北京科技大学 付冬梅 10 (2) 二维高斯 RBF 自变量 ( , ) 1 2 u u u 、中心 ( , ) 1 2 c c c 、 标准化参数 ( , ) 1 2 是二维,则有 2 2 2 2 2 2 1 2 1 1 ( ) ( ) 2 1 [ ] exp u c u c R 图(b): 10 ~ 10, 10 ~ 10, u1 u2 ( , ) (0,2), ( , ) (2,4) c c1 c2 σ 1 2 图(c)与图(b)对应: 1 2 ( , ) 1 2 u u u : ( , ) (0,2) c c1 c2 , ( , ) (2,4) 1 2 是椭圆。 (c) 二维(椭圆情况) (b) 二维 图6-5 高斯径向基函数 6-1 径向基函数(RBF)网络结构和模型
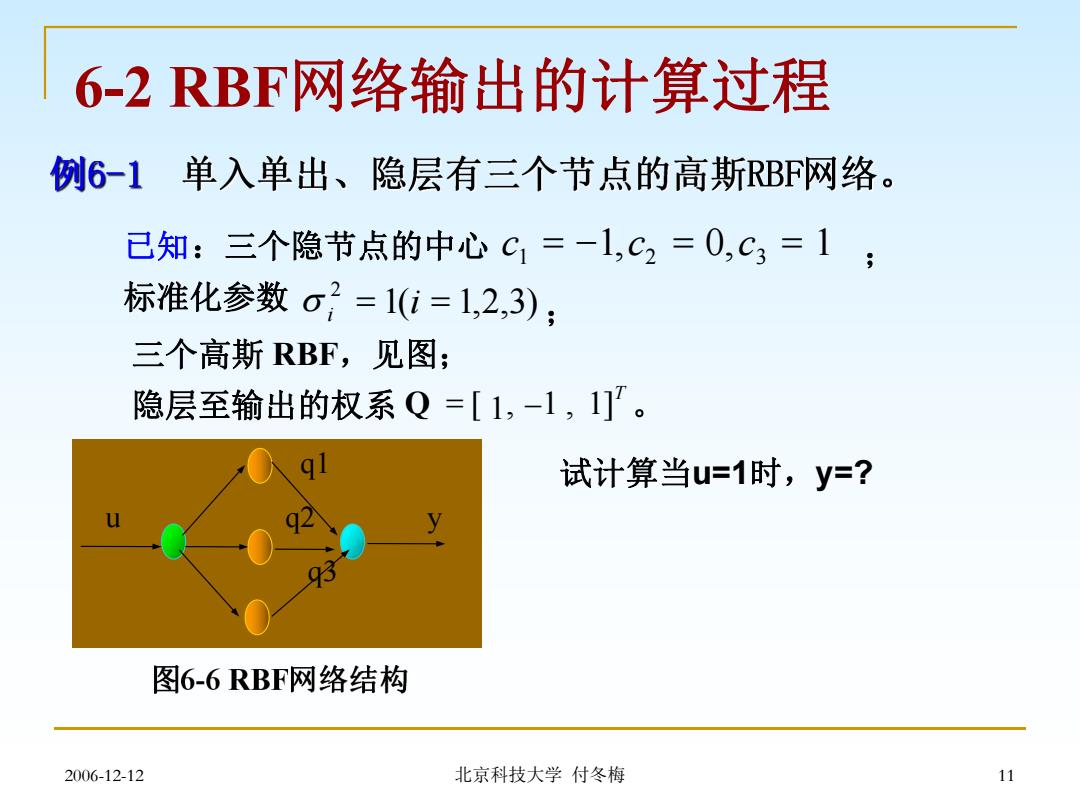
6-2RBF网络输出的计算过程 例6-1单入单出、隐层有三个节点的高斯RBF网络。 已知:三个隐节点的中心C1=-1,C2=0,C3=1; 标准化参数o=1(i=1,2,3); 三个高斯RBF,见图; 隐层至输出的权系Q=[1,-1,1]。 试计算当u=1时,y=? 图6-6RBF网络结构 2006-12-12 北京科技大学付冬梅 11
2006-12-12 北京科技大学 付冬梅 11 1 6-2 RBF网络输出的计算过程 q1 u q2 y q3 已知:三个隐节点的中心 c1 1,c2 0,c3 1 ; 标准化参数 1( 1,2,3) 2 i i ; 三个高斯 RBF,见图; 隐层至输出的权系 T Q [ , 1 , 1] 。 试计算当u=1时,y=?