
第三章:感知柔网络 ·单个感知器模型与解决问题的能力 口单层感知器模型与解决问题的能力 ■单层感知器的学习算法 ■单层感知器的局限性问题 口多层感知器的设计方法 ■有关的几个问题的讨论 ■单层感知器的MATLAB设计与实现
单个感知器模型与解决问题的能力 单层感知器模型与解决问题的能力 单层感知器的学习算法 单层感知器的局限性问题 多层感知器的设计方法 有关的几个问题的讨论 单层感知器的MATLAB设计与实现 第三章:感知器网络

·概述 -由美国学者Rosenblatt在1957年首次提出 -学习算法是Rosenblatt在1958年提出的 -包含一个突触权值可调的神经元 - 属于前向神经网络类型 一只能区分线性可分的模式 perceptron - IEEE设立以其名字命名的奖项 ROSENBLATT AWARD
• 概述 – 由美国学者Rosenblatt在1957年首次提出 – 学习算法是Rosenblatt在1958年提出的 – 包含一个突触权值可调的神经元 – 属于前向神经网络类型 – 只能区分线性可分的模式 – IEEE设立以其名字命名的奖项

第三章:感知恐 ·人的视觉是重要的感觉器官,人通过视觉接受 的信息占全部信息量的80~85%。 感知器是模拟人的视觉,接受环境信息,并由 神经冲动进行信息传递的神经网络 感知器分单层与多层,是具有学习能力的神经 网络。 ·本章的重点: 感知器的结构、表达能力、学习算法。 。本章的难点: 感知器的表达能力
第三章:感知器 ▪ 人的视觉是重要的感觉器官,人通过视觉接受 的信息占全部信息量的80~85%。 ▪ 感知器是模拟人的视觉,接受环境信息,并由 神经冲动进行信息传递的神经网络。 ▪ 感知器分单层与多层,是具有学习能力的神经 网络。 • 本章的重点: 感知器的结构、表达能力、学习算法。 • 本章的难点: 感知器的表达能力

第三章:感知恐 31单个感知器模型与解决问题的能力 是具有单层处理单元的神经网络,非线性作用函数(·)是对称 型阶跃函数,见图。 感知器输出: y=f(∑w,4-0=f∑w,4,) i=0 4:感知器的第i个输入;w。=-0(阈值);4,=1。 与MP模型不同之处: 权值由有导师的学习算法进行调整。 f(x) f(x) 图2-3-1单层感知器
第三章:感知器 3.1 单个感知器模型与解决问题的能力 是具有单层处理单元的神经网络,非线性作用函数f (•) 是对称 型阶跃函数,见图。 感知器输出: y f w u f w u j j j n j j j n = − = = = ( ) ( ) 1 0 u j:感知器的第 j 个输入;w0 = − (阈值);u0 = 1 。 与 MP 模型不同之处: 权值由有导师的学习算法进行调整。 图2-3-1 单层感知器 n j u u u1 y x wn w1 f (x) f (x)
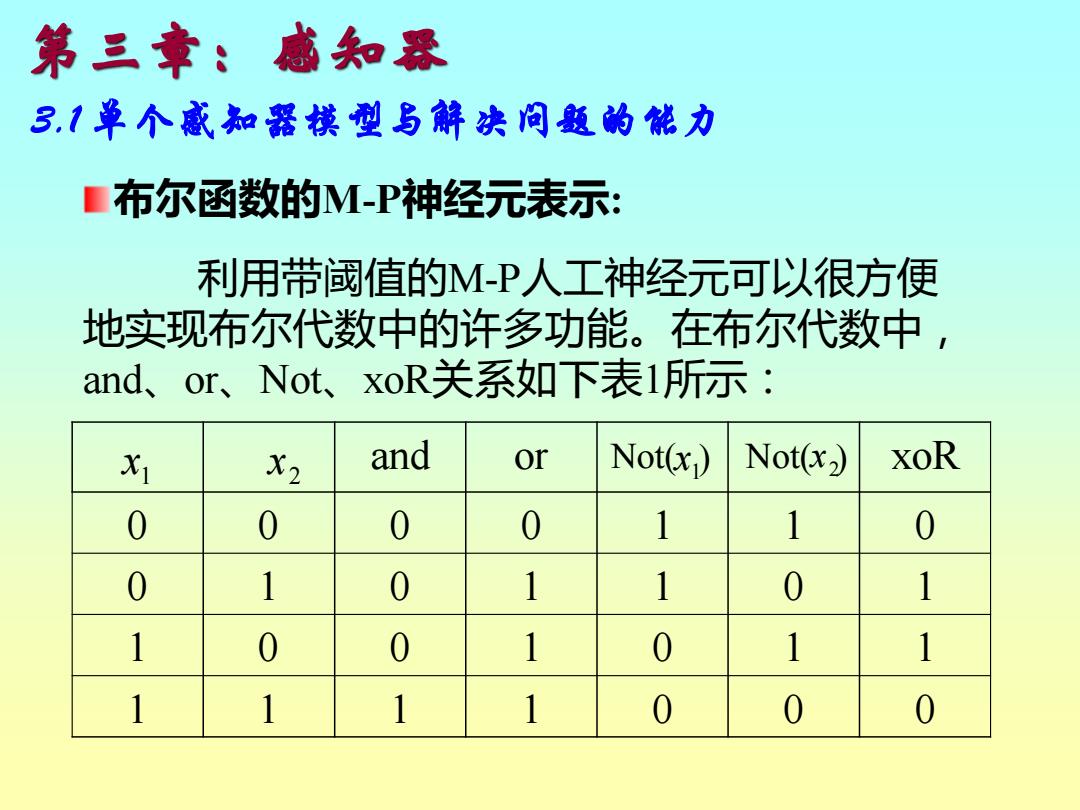
第三章:感知器 3.1单个感知器模型与解决问题的能力 布尔函数的M-P神经元表示: 利用带阈值的M-P人工神经元可以很方便 地实现布尔代数中的许多功能。在布尔代数中, and、or、Not、xoR关系如下表1所示: X1 X2 and or Not(x Not(x) XoR 0 0 0 0 1 1 0 0 1 0 1 1 0 1 1 0 0 1 0 1 1 1 1 1 1 0 0 0
布尔函数的M-P神经元表示: 利用带阈值的M-P人工神经元可以很方便 地实现布尔代数中的许多功能。在布尔代数中, and、or、Not、xoR关系如下表1所示: 第三章:感知器 3.1 单个感知器模型与解决问题的能力 1 x 2 and or ) x ) xoR 0 0 0 0 1 1 0 0 1 0 1 1 0 1 1 0 0 1 0 1 1 1 1 1 1 0 0 0 2 x 1 x Not( Not(
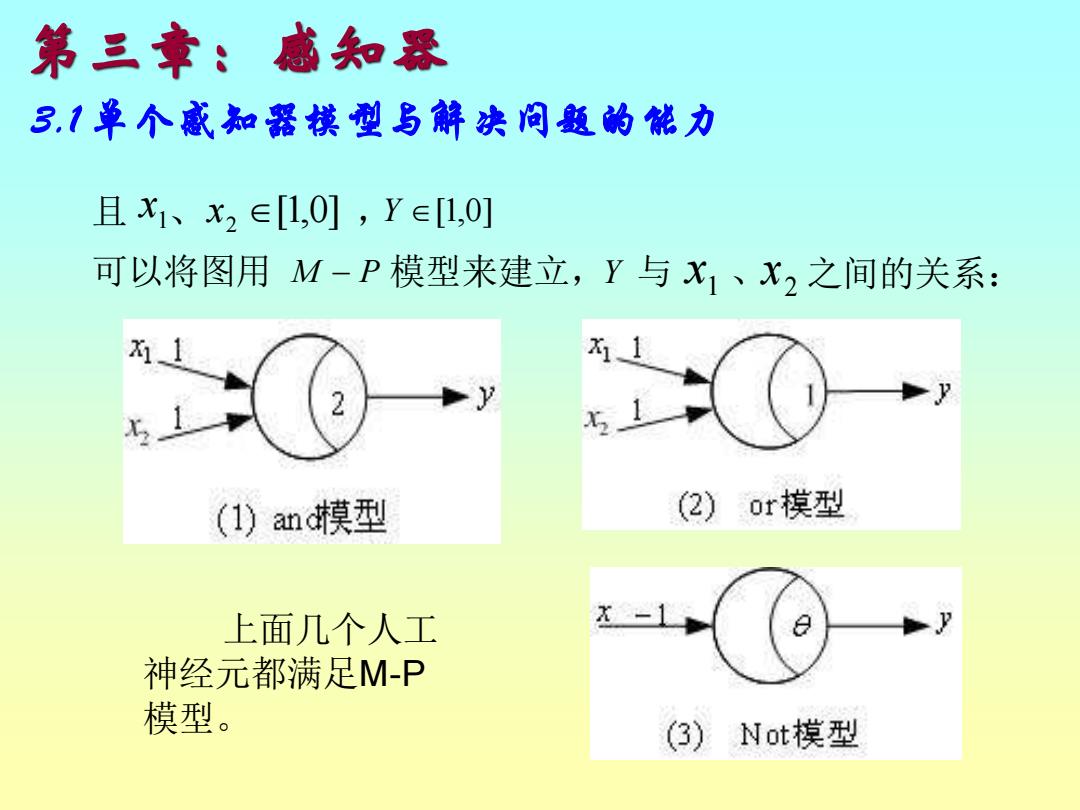
第三章:感知恐 3.1单个感知器模型与解决问题的能力 且x1、x2∈[1,0],Y∈[1,0] 可以将图用M-P模型来建立,Y与X1、X2之间的关系: 五1 11 (1)anc模型 (2)or模型 上面几个人工 神经元都满足M-P 模型。 (3) Not模型
第三章:感知器 3.1 单个感知器模型与解决问题的能力 1 x [1,0] 且 、 x2 , Y [1,0] M − P 模型来建立, Y 1 x 2 可以将图用 与 、 x 之间的关系: 上面几个人工 神经元都满足M-P 模型

第三章:感知聚 31单个感知器模型与解决问题的能力 根据各个图及M-P模型,我们有 少-/+-2)-{0 x1+x2-2≥0 (1) x1+x2-2<0 -{0eKo00,0o (x1,x2)∈{(1,1)} x+x2-1≥0 (2)》 y= fx+x2-)={0 x1+x2-1<0 (x1,x2)∈{(1,1),(1,0),(0,1)} 0 (x1,x2)∈{(0,0)}
第三章:感知器 3.1 单个感知器模型与解决问题的能力 根据各个图及M-P模型,我们有 0 ( , ) {(0,0),(0,1),(1,0)} 1 ( , ) {(1,1)} 0 2 0 1 2 0 ( 2) 1 2 1 2 1 2 1 2 1 2 { { = + − + − = + − = x x x x x x x x ( y f x x 1) (2) 1 2 1 2 1 2 1 2 1 2 1 1 0 ( 1) { 0 1 0 1 ( , ) {(1,1),(1,0),(0,1)} { 0 ( , ) {(0,0)} x x y f x x x x x x x x + − = + − = + − =

第三章:感知景 31单个感和器模型与解决问题的能力 6y=-=09 -0em 显然是符合逻辑运算要求
第三章:感知器 3.1 单个感知器模型与解决问题的能力 0 {1} 1 {0} 0 0 1 0 ( ) { { = − − = − = x x x x (3) y f x 显然是符合逻辑运算要求

第三章:感知器 3,1单个感知器模型与解决问题的能力 权系数和阈值不是0、1的M-P模型 若w,O}∈R,则M-P模型比只允许w取{-1,1}要灵活 的多,但此时仍限制x∈{1,-1(或{1,0}),y∈L,-1 (或{1,0}),则对于这个M-P人工神经元来说: n+l wx,≥0 2地 i=1 n+1 -1 W,x,<0 i-l 但{w,}∈R与w,0}eZ相比并无多大改进
第三章:感知器 3.1 单个感知器模型与解决问题的能力 权系数和阈值不是0、1的M-P模型 w,R w x{1,−1} y {1,−1} 若 ,则M-P模型比只允许 取{-1,1}要灵活 (或{1,0}), (或{1,0}),则对于这个M-P人工神经元来说: 的多,但此时仍限制 − = − = + = + = = 1 1 1 1 1 1 0 1 0 ( ) n i i i n i i i i n i i w x w x y f x w 但 w, R 与w,Z 相比并无多大改进

第三章:感知器 3.1单个感知器模型与解决问题的能力 例:试说明下列两个M-P人工神经元是等价的。 X 0.4 X2 -0.2 0.6 X2 -2 6 0.3 31 3 (a) ) 分析:对于(a) y=f(0.4x1+0.3x3-0.2x2-0.6) 10.4x+0.3x3-0.2x2-0.6≥0 -10.4x+0.3x3-0.2x2-0.6<0 14x-2x32+3x-6≥0 -14x1-2x2+3x3-6<0
第三章:感知器 3.1 单个感知器模型与解决问题的能力 例:试说明下列两个M-P人工神经元是等价的。 分析:对于(a) − − + − − + − = − + − − + − − = = + − − 1 4 2 3 6 0 1 4 2 3 6 0 1 0.4 0.3 0.2 0.6 0 1 0.4 0.3 0.2 0.6 0 (0.4 0.3 0.2 0.6) 1 2 3 1 2 3 1 3 2 1 3 2 1 3 2 x x x x x x x x x x x x y f x x x