
第七章PID神经网络的讲述内容 7.1绪论 7.2PID神经元的计算方法 73PID神经元网络 7.4SPID网络的反传算法 7.5PID网络初值权重的选取和等价系统
7.1 绪论 7.2 PID神经元的计算方法 7.3 PID神经元网络 7.4 SPID网络的反传算法 7.5 PID网络初值权重的选取和等价系统 第七章 PID神经网络的讲述内容

7.1绪论 1)传统控制系统的局限性 由于被控对象的复杂性、大规模和确定性、分布性,要实现自 动控制,那么基于传统精确数学模型的控制理论就显现出极大的 局限性。 传统的控制理论虽然也有办法对付控制对象的不确定性和复杂 性,如自适应控制和鲁棒控制。自适应控制是以自动调节控制器 的参数,使其与被控对象和环境达到良好的“匹配”,以削弱不 确定性的影响。从本质上说,自适应控制是通过估计系统某些重 要参数,以补偿的方法克服系统参数在一定范围内的慢变化。鲁 棒控制是在一定的外部干扰和内部参数变化作用下,以提高系统 的灵敏度为宗旨来抵御不确定性的。根据这一思想和原则所导出 的算法,其鲁棒的区域是很有限的
7.1 绪论 1)传统控制系统的局限性 由于被控对象的复杂性、大规模和确定性、分布性,要实现自 动控制,那么基于传统精确数学模型的控制理论就显现出极大的 局限性。 传统的控制理论虽然也有办法对付控制对象的不确定性和复杂 性,如自适应控制和鲁棒控制。自适应控制是以自动调节控制器 的参数,使其与被控对象和环境达到良好的“匹配”,以削弱不 确定性的影响。从本质上说,自适应控制是通过估计系统某些重 要参数,以补偿的方法克服系统参数在一定范围内的慢变化。鲁 棒控制是在一定的外部干扰和内部参数变化作用下,以提高系统 的灵敏度为宗旨来抵御不确定性的。根据这一思想和原则所导出 的算法,其鲁棒的区域是很有限的

7.1绪论 2)人工神经网络控制的系统的特点和弱点: 般神经网络的弱点,包括以下问题: (①)一般神经元网络的学习和训练时间很长。 (2)由于神经网络结构确定往往要通过反复实验才可能确定,所 以给控制器实际应用方面带来困难。 (3)有的网络在学习时会陷入局部极小(BP),有的网络关键参 数确定有困难(RBF)。 (④)传统系统神经网络的结构、参数和机能,难以与控制系统所 要求的响应快、超调小、无静差、静态指标相联系。 (⑤)传统的多层前向神经网络的神经元仅具有静态输入输出特性, 用它构成控制系统时必须附加其它动态部件
7.1 绪论 2)人工神经网络控制的系统的特点和弱点: 一般神经网络的弱点,包括以下问题: ⑴ 一般神经元网络的学习和训练时间很长。 ⑵ 由于神经网络结构确定往往要通过反复实验才可能确定,所 以给控制器实际应用方面带来困难。 ⑶ 有的网络在学习时会陷入局部极小(BP),有的网络关键参 数确定有困难(RBF)。 ⑷ 传统系统神经网络的结构、参数和机能,难以与控制系统所 要求的响应快、超调小、无静差、静态指标相联系。 ⑸ 传统的多层前向神经网络的神经元仅具有静态输入输出特性, 用它构成控制系统时必须附加其它动态部件

7.1绪论 3)PID控制的特点及其和神经元网络的结合 )=ke()+kJe(dr+k de(1) k,k配令适应.可得到快速敏捷平稳准确的调节效果.但其 合理、快速、实时的确定是关键。 PID在本质上是线性控制规律,具有传统控制理论的弱 点 只适合于线性SSO系统,在复杂系统中控制效果不
7.1 绪论 3)PID控制的特点及其和神经元网络的结合 0 ( ) ( ) ( ) ( ) t P I D de t u t k e t k e d k dt = + + , , P I D k k k 配合适应.可得到快速敏捷.平稳准确的调节效果.但其 合理、快速、实时的确定是关键。 PID在本质上是线性控制规律,具有传统控制理论的弱 点——只适合于线性SISO系统,在复杂系统中控制效果不 佳

7.1绪论 神经元网络和PID控制结合的两种流行方法: r(0 ☒ 被控对象 缺点:结构复杂、不 能避免神经网络自身 的缺陷。 神经网络 缺点 a:仍是选择PID参数的方法。 被控对象 6神经元起的作用相当于单 层感知器,只具有线性分类能
7.1 绪论 神经元网络和PID控制结合的两种流行方法: 被控对象 神经网络 − d dt P k I k Dk rt( ) yt() 被控对象 − d dt W1 W2 W3 rt( ) yt( ) et( ) 缺点:结构复杂、不 能避免神经网络自身 的缺陷。 缺点: a:仍是选择PID参数的方法。 b:神经元起的作用相当于单 层感知器,只具有线性分类能 力

7.1绪论 4)PID神经元网络(PIDNN)的特点和结构形式 PIDNN的主要特点如下; ■PIDNN属于交层前向神经元网络; ■PIDNN参照PID控制规律构成,结构比较简单、规范。 ■PIDNN的初值按PID控制规律的基本原侧确定,加快了 收敛速度,不易陷入极小点,更重要的是可以利用现有 的PID控制的大量经验数据确定网络权重初值,使控制 系统保持初始稳定,使系统的全局稳定成为可能。 PIDNN可采用"无教师”的学习方式,根据控制效果进 行在线自学习和调整,使系统具备较好的性能。 ■PIDNN可同时适用于SISO以及MIMO控制系统
7.1 绪论 4)PID神经元网络(PIDNN)的特点和结构形式 PIDNN的主要特点如下; ◼ PIDNN属于交层前向神经元网络; ◼ PIDNN参照PID控制规律构成,结构比较简单、规范。 ◼ PIDNN的初值按PID控制规律的基本原则确定,加快了 收敛速度,不易陷入极小点;更重要的是可以利用现有 的PID控制的大量经验数据确定网络权重初值,使控制 系统保持初始稳定,使系统的全局稳定成为可能。 ◼ PIDNN可采用“无教师”的学习方式,根据控制效果进 行在线自学习和调整,使系统具备较好的性能。 ◼ PIDNN可同时适用于SISO以及MIMO控制系统
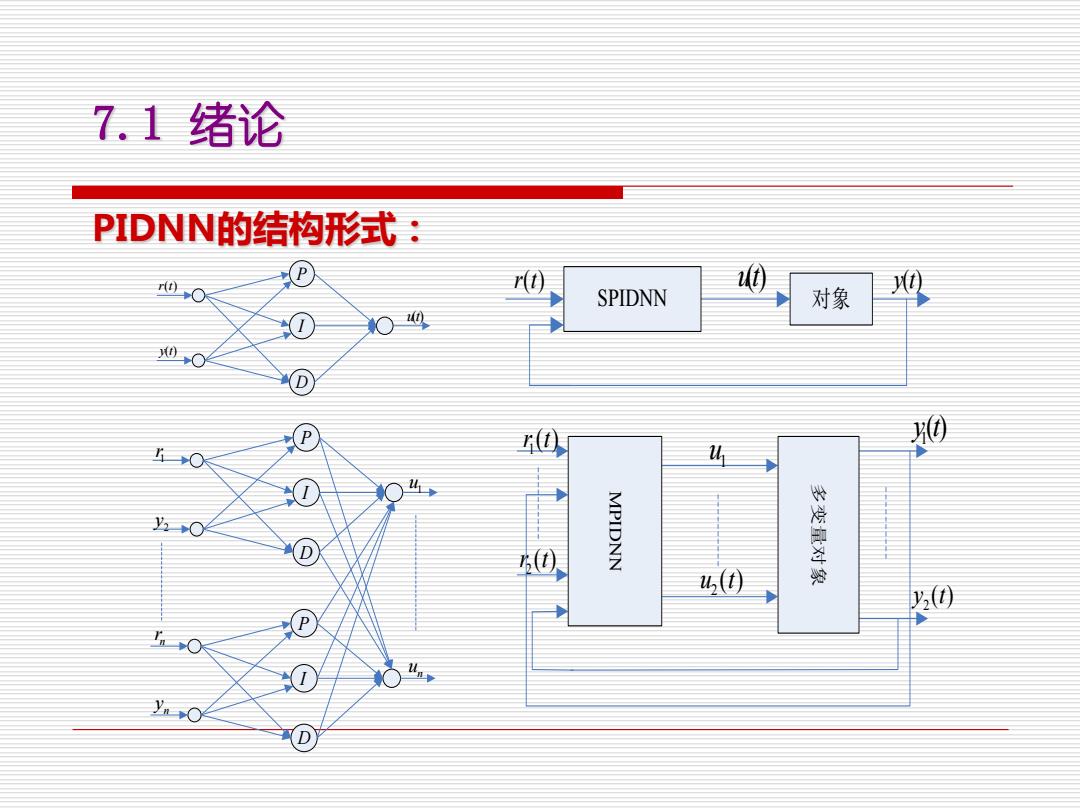
7.1绪论 PIDNN的结构形式: P r(1) ⑩ SPIDNN 对象 ① D u MPIDNN u(t) (0 yO
PIDNN的结构形式: 7.1 绪论 P ID rt() yt() ut() r t( ) ut() yt( ) SPIDNN 对象 P ID P ID 1r 2 y n r n y 1 u n u 1r t( ) 1 u 2r t( ) 2 u t( ) 2 y t( ) 1yt() MPIDNN 多变量对象

7,2PID神经元的计算方法 1)比例元 O比例元的输入为4因=冕,W ② 比例元的状态函数4,()=net,( ③比例元的输出函数 1 u()>1 向=以优】=u() -1≤u()≤1 -1 u,(份<-1
7.2 PID神经元的计算方法 ① 比例元的输入为 1 1 ( ) ( ) n j ij i j net k w x k − = = 1) 比例元 ② 比例元的状态函数 ( ) ( ) j j u k net k = ③ 比例元的输出函数

7.2PID神经元的计算方法 2)积分元 u(k)=g,[net,(k),u,(k-1]=u,(k-1)+net (k) 积分元的输入和输出函数与比例函数相同。 3)微分元 u,(k)=golnet,(k),net (k-1]=net (k)-net (k-1) 微分元的输入和输出函数与比例函数相同
7.2 PID神经元的计算方法 2) 积分元 ( ) [ ( ), ( 1)] ( 1) ( ) j I i j j j u k g net k u k u k net k = − = − + 积分元的输入和输出函数与比例函数相同。 3) 微分元 ( ) [ ( ), ( 1)] ( ) ( 1) j D j j j j u k g net k net k net k net k = − = − − 微分元的输入和输出函数与比例函数相同

7.3PID神经元网络 将PID和一般神经元网络融合起来的方法包括两个步骤: ①将PID功能引入神经网络的神经元中,构成PID神经元 (第二节完成); ②. 按照PID神经元的控制规律的基本模式,用这些基本神 经元构成新的神经元网络,并找到合理有效的计算与学 习方法(下节完成)
7.3 PID神经元网络 将PID和一般神经元网络融合起来的方法包括两个步骤: ① 将PID功能引入神经网络的神经元中,构成PID神经元 (第二节完成); ② 按照PID神经元的控制规律的基本模式,用这些基本神 经元构成新的神经元网络,并找到合理有效的计算与学 习方法(下节完成)