
第1章测试系统特性分析 概述 二 测量误差 测试系统的静态特性 四、 测试系统的动态特性 五、 测试系统实现精确测量的条件 六、测试系统的负载效应
第1章 测试系统特性分析 一、概述 二、测量误差 三、测试系统的静态特性 四、测试系统的动态特性 五、测试系统实现精确测量的条件 六、测试系统的负载效应

概述 。信号与系统紧密相关。 被测的物理量亦即信号作用于一个测试系统, 而该系统在输入信号亦即激励的驱动下对它 进行“加工”,并将经“加工”后的信号进 行输出。 输出信号的质量必定差于输入信号的质量。 受测试系统的特性影响; 受信号传输过程中干扰的影响
一、概述 ⚫ 信号与系统紧密相关。 ⚫ 被测的物理量亦即信号作用于一个测试系统, 而该系统在输入信号亦即激励的驱动下对它 进行“加工”,并将经“加工”后的信号进 行输出。 ⚫ 输出信号的质量必定差于输入信号的质量。 – 受测试系统的特性影响; – 受信号传输过程中干扰的影响
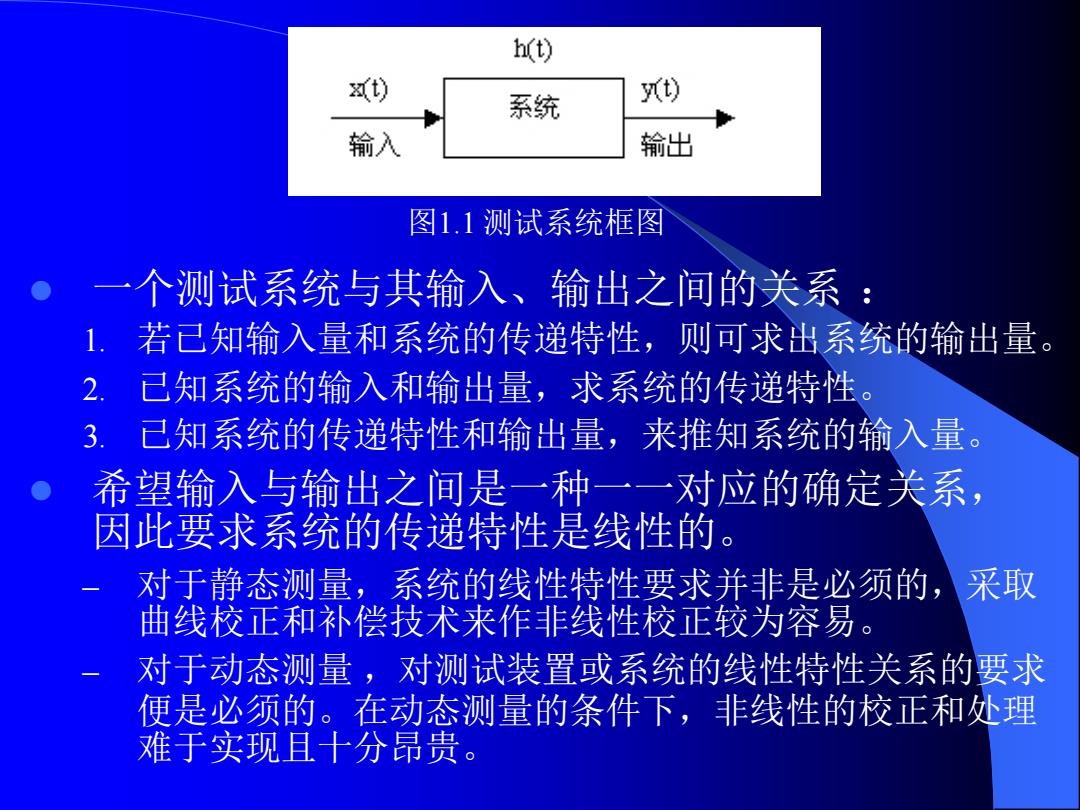
h(t) 式) 系统 y(t) 输入 输出 图1.1测试系统框图 一个测试系统与其输入、输出之间的关系: 1.若已知输入量和系统的传递特性,则可求出系统的输出量。 2.已知系统的输入和输出量,求系统的传递特性。 3. 已知系统的传递特性和输出量,来推知系统的输入量。 希望输入与输出之间是一种一一对应的确定关系, 因此要求系统的传递特性是线性的。 对于静态测量,系统的线性特性要求并非是必须的,采取 曲线校正和补偿技术来作非线性校正较为容易 0 对于动态测量,对测试装置或系统的线性特性关系的要求 便是必须的。在动态测量的条件下,非线性的校正和处理 难于实现且十分昂贵
⚫ 一个测试系统与其输入、输出之间的关系 : 1. 若已知输入量和系统的传递特性,则可求出系统的输出量。 2. 已知系统的输入和输出量,求系统的传递特性。 3. 已知系统的传递特性和输出量,来推知系统的输入量。 ⚫ 希望输入与输出之间是一种一一对应的确定关系, 因此要求系统的传递特性是线性的。 – 对于静态测量,系统的线性特性要求并非是必须的,采取 曲线校正和补偿技术来作非线性校正较为容易。 – 对于动态测量 ,对测试装置或系统的线性特性关系的要求 便是必须的。在动态测量的条件下,非线性的校正和处理 难于实现且十分昂贵。 图1.1 测试系统框图

二、测量误差 。定义: -误差E是指示值与真值或准确值的差: E=Xm-X (1.1) Xm一指示值; x一真值或准确值。 校正值或修正值B是与误差E的数值相等但符号 相反的值: B-X-Xm (1.2)
二、测量误差 ⚫ 定义: – 误差E是指示值与真值或准确值的差: E=xm-x (1.1) xm-指示值; x-真值或准确值。 – 校正值或修正值B是与误差E的数值相等但符号 相反的值 : B=x-xm (1.2)

。分类一(根据误差的性质): 系统误差: 定义:每次测量同一量时,呈现出相同的或确定性方 式的那些测量误差。 ● 产生原因:由标定误差、持久发生的人为误差、不良 仪器造成的误差、负载产生的误差、系统分辨率局限 产生的误差等因素所产生。 随机误差: ● 定义:每次测量同一量时,其数值均不一致、但却具 有零均值的那些测量误差。 产生的原因有:测量人员的随机因素、设备受干扰、 实验条件的波动、测量仪器灵敏度不够等。 -过失误差或非法误差: 。意想不到而存在的误差。 ● 如实验中因过失或错误引起的误差,实验之后的计算 误差等
⚫ 分类一(根据误差的性质): – 系统误差: ⚫ 定义:每次测量同一量时,呈现出相同的或确定性方 式的那些测量误差。 ⚫ 产生原因:由标定误差、持久发生的人为误差、不良 仪器造成的误差、负载产生的误差、系统分辨率局限 产生的误差等因素所产生。 – 随机误差: ⚫ 定义:每次测量同一量时,其数值均不一致、但却具 有零均值的那些测量误差。 ⚫ 产生的原因有:测量人员的随机因素、设备受干扰、 实验条件的波动、测量仪器灵敏度不够等。 – 过失误差或非法误差: ⚫ 意想不到而存在的误差。 ⚫ 如实验中因过失或错误引起的误差,实验之后的计算 误差等
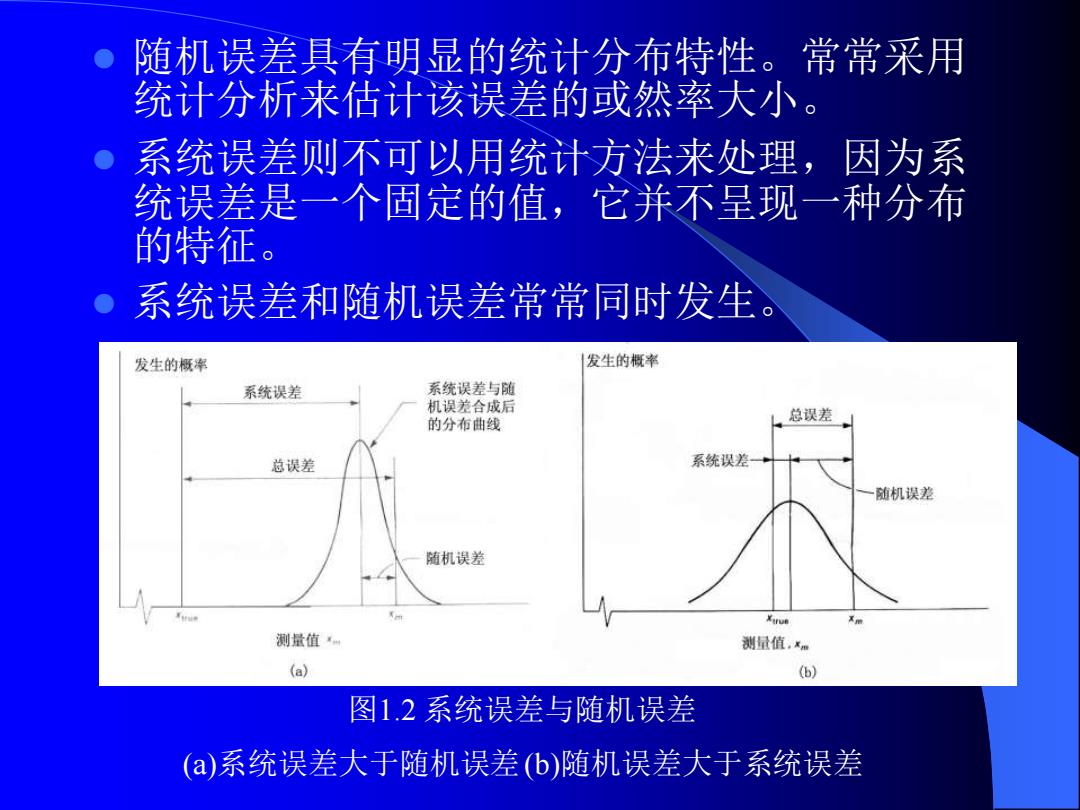
随机误差具有明显的统计分布特性。常常采用 统计分析来估计该误差的或然率大小。 系统误差则不可以用统计方法来处理,因为系 统误差是一个固定的值,它并不呈现一种分布 的特征。 系统误差和随机误差常常同时发生 发生的概率 发生的概率 系统误差 系统误差与随 机误差合成后 的分布曲线 总误差 总误差 系统误差· 随机误差 随机误差 Xurue 测量值 测量值,m (a) 6) 图1.2系统误差与随机误差 (a)系统误差大于随机误差(b)随机误差大于系统误差
⚫ 随机误差具有明显的统计分布特性。常常采用 统计分析来估计该误差的或然率大小。 ⚫ 系统误差则不可以用统计方法来处理,因为系 统误差是一个固定的值,它并不呈现一种分布 的特征。 ⚫ 系统误差和随机误差常常同时发生。 图1.2 系统误差与随机误差 (a)系统误差大于随机误差(b)随机误差大于系统误差

。分类二(根据测量的类型): -静态误差: 。定义:用来确定时不变测量值的线性测量仪器, 其传递特性为一常数。而相应的非线性测量仪器 的输入一输出关系是用代数方程或超越方程来 描述的。因而所产生的误差一般仅取决于测量值 大小而其本身不是时间的函数。这种误差称静态 误差。 动态误差: 。定义:在测量时变物理量时,要用微分方程来描 述输入—输出关系。此时产生的误差不仅取决 于测量值的大小,而且还取决于测量值的时间过 程。将这种误差称动态误差
⚫ 分类二(根据测量的类型): – 静态误差: ⚫ 定义:用来确定时不变测量值的线性测量仪器, 其传递特性为一常数。而相应的非线性测量仪器 的输入——输出关系是用代数方程或超越方程来 描述的。因而所产生的误差一般仅取决于测量值 大小而其本身不是时间的函数。这种误差称静态 误差。 – 动态误差: ⚫ 定义:在测量时变物理量时,要用微分方程来描 述输入——输出关系。此时产生的误差不仅取决 于测量值的大小,而且还取决于测量值的时间过 程。将这种误差称动态误差

三、测试系统的静态特性 当被测量是恒定的、或是慢变的物理量 时,涉及到系统的静态特性。 静态特性包括: 1.重复性 2.漂移: 3.误差 4.精确度: 5.分辨率 6.线性度; 7.非线性
三、测试系统的静态特性 ⚫ 当被测量是恒定的、或是慢变的物理量 时 ,涉及到系统的静态特性。 ⚫ 静态特性包括: 1. 重复性; 2. 漂移; 3. 误差; 4. 精确度; 5. 分辨率; 6. 线性度; 7. 非线性

重复性(亦称精度): 表示由同一观察者采用相同的测量条件、方法及仪器 对同一被测量所做的一组测量之间的接近程度。 表征测量仪器随机误差接近于零的程度。 漂移: 仪器的输入未产生变化时其输出所发生的变化。 由仪器的内部温度变化和元件的不稳定性引起。 2 误差: 仪器的误差有两种表达方式: 绝对误差:用专门的测量单位来表示; 相对误差:表达为被测量的一个百分比值,或表达 为某个专门值比如满量程指示值的一个百分比
1. 重复性(亦称精度): • 表示由同一观察者采用相同的测量条件、方法及仪器 对同一被测量所做的一组测量之间的接近程度。 • 表征测量仪器随机误差接近于零的程度。 2. 漂移: • 仪器的输入未产生变化时其输出所发生的变化。 • 由仪器的内部温度变化和元件的不稳定性引起。 3. 误差: • 仪器的误差有两种表达方式: ✓ 绝对误差:用专门的测量单位来表示; ✓ 相对误差:表达为被测量的一个百分比值,或表达 为某个专门值比如满量程指示值的一个百分比

精确度: 测量仪器的指示值和被测量真值的符合 程度,通过所宣称的概率界限将仪器输 出与被测量的真值关联起来 精确度是由诸如非线性、迟滞、温度变 化、漂移等一系列因素所导致的不确定 度之和。 5 灵敏度: 单位被测量引起的仪器输出值的变化 灵敏度有时亦称增益或标度因子
4. 精确度: • 测量仪器的指示值和被测量真值的符合 程度,通过所宣称的概率界限将仪器输 出与被测量的真值关联起来。 • 精确度是由诸如非线性、迟滞、温度变 化、漂移等一系列因素所导致的不确定 度之和。 5. 灵敏度: – 单位被测量引起的仪器输出值的变化。 – 灵敏度有时亦称增益或标度因子