
第六章 状态反馈和状态观测器
第六章 状态反馈和状态观测器

6.1引言 (1)研究自动控制系统有三大命题:模型、分析和综合。 前面几章讨论的是线性系统数学模型的建立,以及系统的分 析问题。 系统的分析是已知系统的结构参数,在外界输入或扰动作 用下,定量或定性分析系统的性能(系统的响应、 稳定性、 和能控行、能观性)问题 系统的综合也称系统的设计问题,与系统分析相反,它是 在给定系统基本结构、参数的前提下,设计一种控制器,它 产生的控制作用能使系统达到期望的性能。 系统的控制有两种:开环控制和闭环控制(反馈控制)。 反馈控制对于系统抗干扰和抗参数变动等方面均有较强的作 用,被广泛应用。反馈有两种形式:状态反馈与输出反馈
6.1 引 言 ⑴ 研究自动控制系统有三大命题:模型、分析和综合。 系统的综合也称系统的设计问题,与系统分析相反,它是 在给定系统基本结构、参数的前提下,设计一种控制器,它 产生的控制作用能使系统达到期望的性能。 前面几章讨论的是线性系统数学模型的建立,以及系统的分 析问题。 系统的分析是已知系统的结构参数,在外界输入或扰动作 用下,定量或定性分析系统的性能(系统的响应、稳定性、 和能控行、能观性)问题 系统的控制有两种:开环控制和闭环控制(反馈控制)。 反馈控制对于系统抗干扰和抗参数变动等方面均有较强的作 用,被广泛应用。 反馈有两种形式:状态反馈与输出反馈

2)状态反馈 在状态空间描述中,系统的状态包含了系统的所有重要 信息,如果系统的反馈信号取之于系统状态或系统输出, 无疑将会获得性能更好的控制。这就是状态反馈。 图6-1是系统控制作用 系统 M是由状态反馈和参考输 A,B,C,D -Kx 入组成的状态反馈系统结 构方块图。 本章将会论及,如果系 控制器 统是能控的,就可以通过 K 选择适当的K来任意配置 系统的极,点。 图6-1
在状态空间描述中 ,系统的状态包含了系统的所有重要 信息,如果系统的反馈信号取之于系统状态或系统输出, 无疑将会获得性能更好的控制。这就是状态反馈。 ( ) 系 统 A,B,C, D K 控制器 x r + −Kx u y 图6-1 图6-1是系统控制作用 是由状态反馈和参考输 入组成的状态反馈系统结 构方块图。 本章将会论及,如果系 统是能控的,就可以通过 选择适当的 来任意配置 系统的极点 。 K u ⑵ 状态反馈
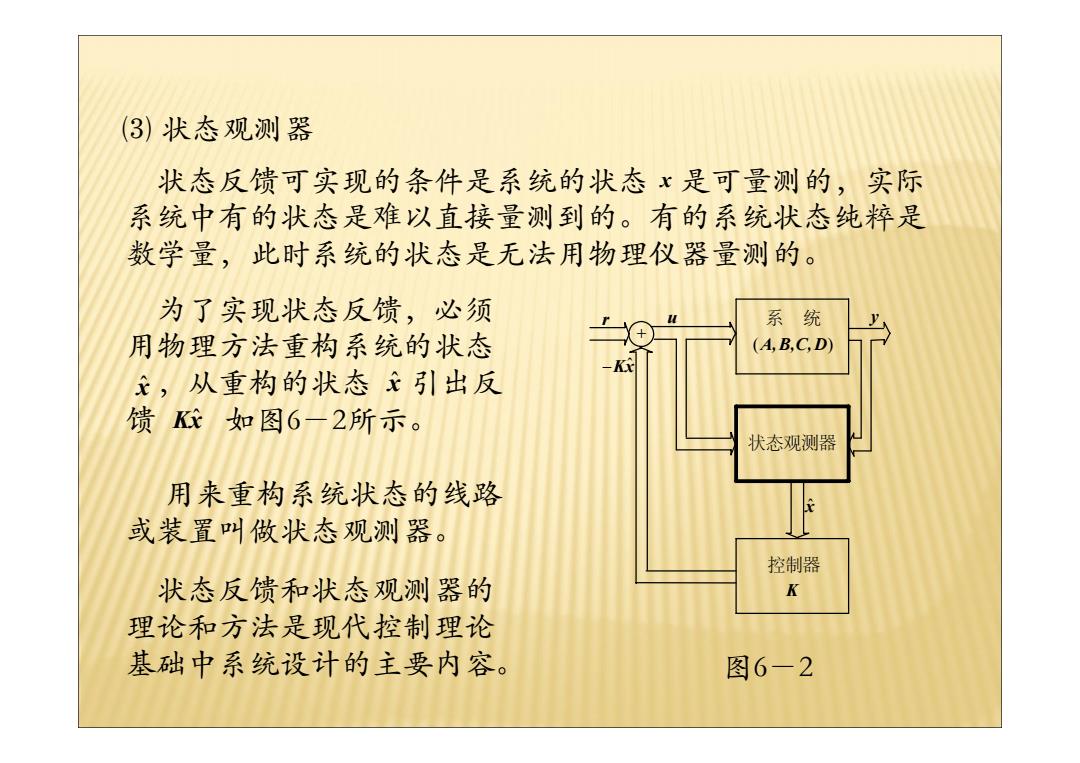
3)状态观测器 状态反馈可实现的条件是系统的状态x是可量测的,实际 系统中有的状态是难以直接量测到的。有的系统状态纯粹是 数学量,此时系统的状态是无法用物理仪器量测的。 为了实现状态反馈,必须 系统 用物理方法重构系统的状态 (A,B,C,D) ,从重构的状态引出反 馈配如图6-2所示。 状态观测器 用来重构系统状态的线路 或装置叫做状态观测器。 控制器 状态反馈和状态观测器的 K 理论和方法是现代控制理论 基础中系统设计的主要内容。 图6-2
⑶ 状态观测器 状态反馈可实现的条件是系统的状态 是可量测的,实际 系统中有的状态是难以直接量测到的。有的系统状态纯粹是 数学量,此时系统的状态是无法用物理仪器量测的。 x 状态观测器 K 控制器 x ˆ r + −Kxˆ u (A,B,C,D) 系 统 y 图6-2 为了实现状态反馈,必须 用物理方法重构系统的状态 ,从重构的状态 引出反 馈 如图6-2所示。 x ˆ x ˆ Kxˆ 用来重构系统状态的线路 或装置叫做状态观测器。 状态反馈和状态观测器的 理论和方法是现代控制理论 基础中系统设计的主要内容

(4)本章主要内容 ①状态反馈:线性定常系统状态反馈对系统的影响,状态反 馈可任意配置系统极,点的条件和计算方法。 ② 状态观测器:状态观测器能重构状态的条件和设计方法。 用求解西尔维斯特(Sylvester)方程的方法设计 状态反馈和状态观测器。 ③状态反馈的应用:系统的镇定、系统解耦和无静差跟踪系 统的综合问题 ④线性二次型最优控制的理论及设计控制器的方法
① 状态反馈:线性定常系统状态反馈对系统的影响, 状态反 馈可任意配置系统极点的条件和计算方法 。 ⑷ 本章主要内容 ② 状态观测器:状态观测器能重构状态的条件和设计方法。 用求解西尔维斯特( )方程的方法设计 状态反馈和状态观测器 。 ③ 状态反馈的应用:系统的镇定 、系统解耦和无静差跟踪系 统的综合问题 ④ 线性二次型最优控制的理论及设计控制器的方法 Sylvester
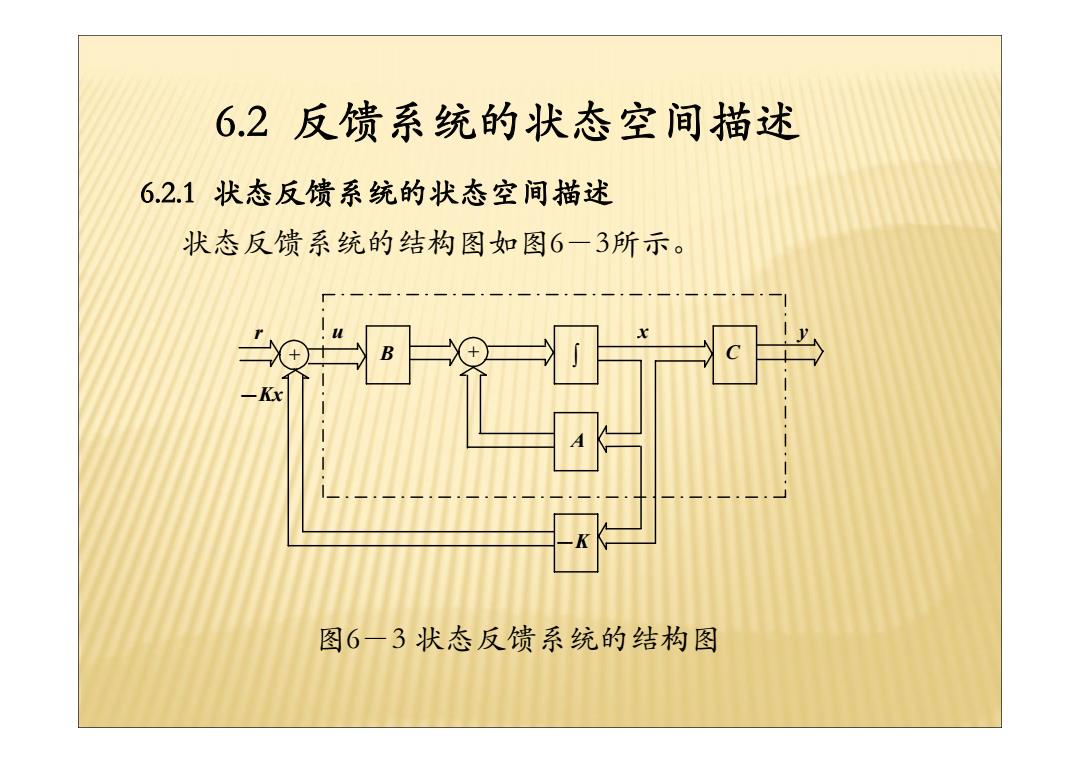
62反馈系统的状态空间描述 6.2.1状态反馈系统的状态空间描述 状态反馈系统的结构图如图6一3所示。 -Kx 图6一3状态反馈系统的结构图
6.2 反馈系统的状态空间描述 A - K B ∫ r u y C x -Kx + + 图6-3 状态反馈系统的结构图 6.2.1 状态反馈系统的状态空间描述 状态反馈系统的结构图如图6-3所示

设原系统的状态空间描述为 ∑: =Ax+Bu (6-1) y=Cx+Du 引入状态反馈,闭环系统的控制规律(输入)为 u=r-Kx (6—2) 式中,r是系统的参考输入,K是p×n状态反馈阵。 闭环系统状态空间描述:将(6一2)代入式(6一1)得 =Ax+B(r-Kx)=(A-BK)x+Br y=Cx+D(r-Kx)=(C-DK)x+Dr 若D=0,则 : 文=(A-BK)x+Br y=Cx
设原系统的状态空间描述为 y Cx Du Σ : x Ax Bu = + & = + 引入状态反馈 ,闭环系统的控制规律(输入)为 Kx u = r -Kx 式中, 是系统的参考输入, 是 状态反馈阵。 r K p × n ( 6-1) ( 6—2) y Cx D r Kx C DK x Dr x Ax B r Kx A BK x Br = + = + = + = + ( ) ( ) ( ) ( ) - - & - - 若 ,则 D = 0 y Cx Σ : x A BK x Br = f & = ( - ) + ( 6—4) ( 6—3) 闭环系统状态空间描述:将( 6-2)代入式( 6-1)得

带状态反馈的闭环系统的传递函数阵为 G(s)=C(sI-(A-BK))-B (6—5) G(s)是q×p阵。 原系统的性能主要由A的特征值(系统的极,点)决定,状态 反馈系统的极,点是A一BK的特征值,有可能通过的选择K来任 意配置系统的极,点
带状态反馈的闭环系统的传递函数阵为 G C I A BK B1 ( ) ( ( )) − f s = s − - ( 6—5) (s) G f 是 阵。 q × p 原系统的性能主要由 的特征值(系统的极点)决定,状态 反馈系统的极点是 的特征值,有可能通过的选择 来任 意配置系统的极点。 A -BK K A

6.2.2 输出反馈系统的状态空间描述 图6一4输出反馈系统的结构图 输出反馈系统的控制规律是 (6-6) 式中,F是pxg输出反馈阵。代入式(6一1)得 =(A-BFC)x+Br y=(C-DFC)x+Dr (6-7)
6.2.2 输出反馈系统的状态空间描述 图6-4输出反馈系统的结构图 输出反馈系统的控制规律是 式中, 是 输出反馈阵。代入式 F p × q ( 6—1) 得 (6-6) + + A B C − F − Fx ∫ r u y x y C DFC x Dr x A BFC x Br = + = + ( ) ( ) - & - (6-7)

若D=0,则有 Ed: =(A-BFC)x+Br (6-8) y=Cx 带输出反馈的闭环系统的传递函数阵为 Gor(s)=C(sI-(A-BFC))-B (6-9) Gg(s)是9×p阵。 原系统的传递函数阵为 G(s)=C(sI-A)B (6-10) 则 G(s)=G(s)(I+FG(s) (6-11) 或 Gr(s)=(I+FG(s))G(s) (6-12) 输出反馈也可以通过F来改变系统的极,点,但它不能像状态 反馈那样任意配置系统的极,点。因为通常方程℉C=K的解不 存在
若 ,则有 D = 0 y Cx Σ : x A BFC x Br = cf & = ( - ) + 带输出反馈的闭环系统的传递函数阵为 G C I A BFC B1 ( ) ( ( ))− cf s = s − - Gcf (s)是 阵。 q× p G C I A B1 ( ) ( ) − s = s − 1 ( ) ( )( ( )) − s = s + s Gcf G I FG 则 ( ) ( ( )) ( ) 1 s s s Gcf I FG G− = + 或 输出反馈也可以通过 来改变系统的极点,但它不能像状态 反馈那样任意配置系统的极点。因为通常方程 的解不 存在。 F FC = K 原系统的传递函数阵为 (6-8) (6-9) (6-10) (6-11) (6-12)