
上誉文通大¥ SHANGHAI JIAO TONG UNIVERSITY 第六章状态反馈与最优控制 6.1问题的提出 目前为止,我们已经: >建立了系统的状态空间模型 >提出了基于状态空间模型的系统的运动分析 >探讨了系统的性能:稳定性、能控性、能观性 用在哪里?->设计控制系统! 系统的控制方式一开环控制、闭环控制(反馈控制)
第六章 状态反馈与最优控制 6.1 问题的提出 目前为止,我们已经: ¾ 建立了系统的状态空间模型 ¾ 提出了基于状态空间模型的系统的运动分析 ¾ 探讨了系统的性能:稳定性、能控性、能观性 用在哪里?->设计控制系统! 系统的控制方式-开环控制、闭环控制(反馈控制)

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 经典控制:只能用系统输出作为反馈控制器的输入 现代控制:由于状态空间模型刻画了系统内部特征,故而 还可用系统内部状态作为反馈控制器的输入 根据用于控制的系统信息:状态反馈、输出反馈 控制系统的动态性能,主要由其状态矩阵的特征值 (即闭环极点)决定 基于状态空间表达式,可以通过形成适当的反馈控 制,进而配置系统的极点,使得闭环系统具有期望的 动态特性
控制系统的动态性能,主要由其状态矩阵的特征值 (即闭环极点)决定 基于状态空间表达式,可以通过形成适当的反馈控 制,进而配置系统的极点,使得闭环系统具有期望的 动态特性 经典控制:只能用系统输出作为反馈控制器的输入 现代控制:由于状态空间模型刻画了系统内部特征,故而 还可用系统内部状态作为反馈控制器的输入 根据用于控制的系统信息:状态反馈、输出反馈
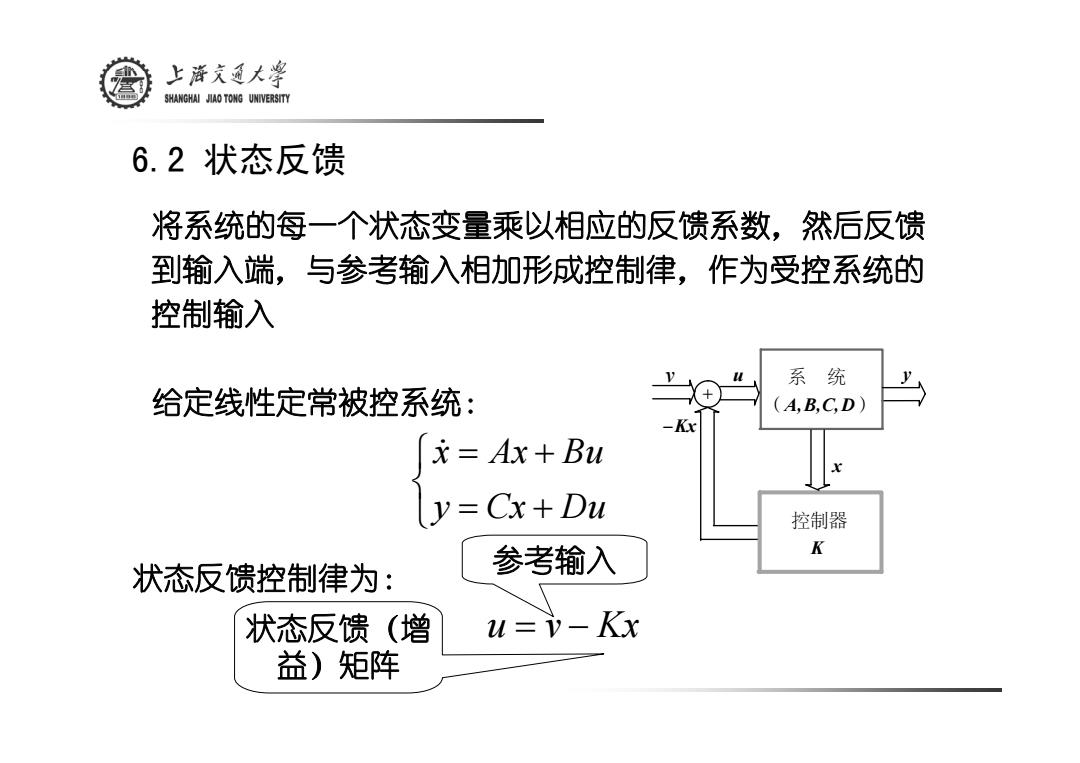
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 6.2状态反馈 将系统的每一个状态变量乘以相应的反馈系数,然后反馈 到输入端,与参考输入相加形成控制律,作为受控系统的 控制输入 系统 给定线性定常被控系统: A,B,C,D) -Kx x=Ax+Bu y=Cx+Du 控制器 参考输入 K 状态反馈控制律为: 状态反馈(增 u=i-Kx 益)矩阵
将系统的每一个状态变量乘以相应的反馈系数,然后反馈 到输入端,与参考输入相加形成控制律,作为受控系统的 控制输入 给定线性定常被控系统: ⎩ ⎨ ⎧ = + = + y Cx Du x& Ax Bu 状态反馈控制律为: 状态反馈(增 益)矩阵 参考输入 6.2 状态反馈 u = v − Kx ( ) 系 统 A,B,C, D K 控制器 x v + −Kx u y
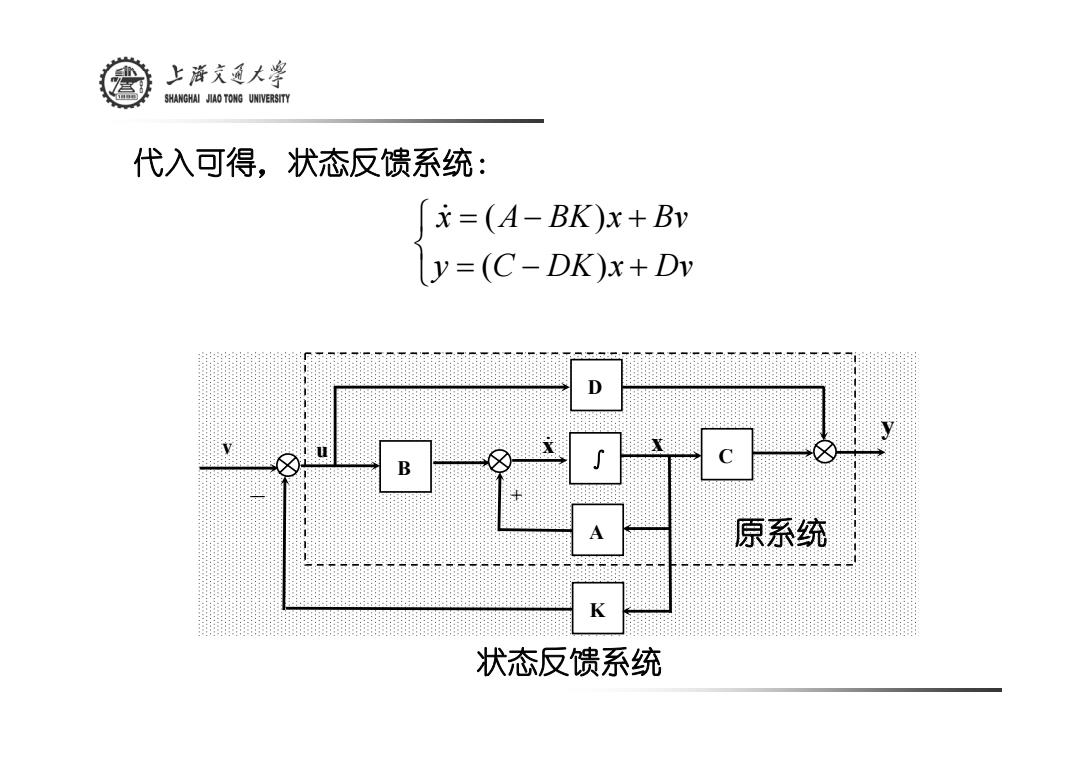
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 代入可得,状态反馈系统: =(A-BK)x+Bv y=(C-DK)x+Dv D B 原系统 K 状态反馈系统
代入可得,状态反馈系统: ∫ v u B C y D A K — + x& x 状态反馈系统 原系统 ⎩ ⎨ ⎧ = − + = − + y C DK x Dv x A BK x Bv ( ) & ( )

上誉文廷大¥ SHANGHAI JIAO TONG UNIVERSITY 若控输入不直接作用到输出,即D=0,则: =(A-BK)x+Bv y=Cx 此时对应的传递函数矩阵为: Gx (s)=C(sI-(A-BKB 对应特征方程: a(2)=2I-A+BK=0 状态反馈阵的引入可以改变闭环系统的特征值,从而使系 统达到所要求的性能
若控制输入不直接作用到输出,即D=0,则: 状态反馈阵 K的引入可以改变闭环系统的特征值,从而使系 统达到所要求的性能 此时对应的传递函数矩阵为: Gk ( s) () C [sI A BK ] B −1 = − − a ( λ) = λI − A + BK = 0 对应特征方程: ⎩ ⎨ ⎧ = = − + y Cx x& ( A BK ) x Bv
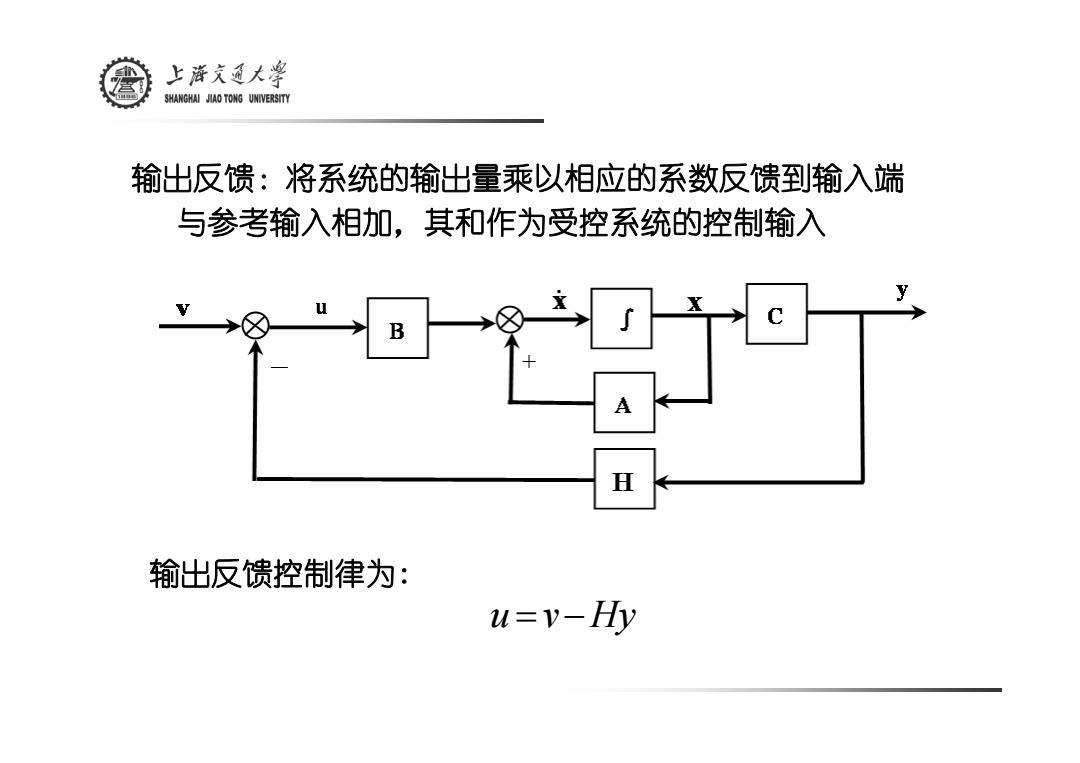
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 输出反馈:将系统的输出量乘以相应的系数反馈到输入端 与参考输入相加,其和作为受控系统的控制输入 B 输出反馈控制律为: u=v-Hy
输出反馈:将系统的输出量乘以相应的系数反馈到输入端 与参考输入相加,其和作为受控系统的控制输入 u = v −Hy 输出反馈控制律为:

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 输出反馈是特殊的状态反馈 当HC=时,输出反馈等同于全状态反馈 输出反馈系统的状态空间表达式为: =Ax+Bu Ax+B(y-Hy) =Ax+By-BHCx=(A-BHCx+Bv y=Cx 对应的传递函数矩阵为: G(s)=C(sI-A+BHC)B
输出反馈系统的状态空间表达式为 : = Ax + Bv − BHCx = ( ) A − BHC x + Bv x& = Ax + Bu = Ax + B ( v − Hy ) y = Cx 输出反馈是特殊的状态反馈 当 HC=K时,输出反馈等同于全状态反馈 对应的传递函数矩阵为: G s C sI A BHC B 1 ( ) ( ) − = − +

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 例6.2.1试给出引入状态反馈K=[10]后闭环系统的状态 空间模型 X二 8®水 解:引入状态反馈:u=v-Kx 则 =(A-BK)x+Bv y=Cx 4a账i0-b-Bd
例6.2.1 试给出引入状态反馈 后闭环系统的状态 空间模型 x x u y [ ] 0 1 x 1 0 1 0 . 0 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = K =[ ] 1 0 解: 引入状态反馈: u = v − Kx ⎩ ⎨ ⎧ = = − + y Cx x& ( A BK ) x Bv 则 [ ] ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ =⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = 0 0 0 1 0 1 0 1 1 0 0 1 A BK

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 作业5试分析引入状态反馈K=[10]前后系统的能控性和 能观性 8d小-p水
作业5 试分析引入状态反馈 前后系统的能控性和 能观性 x x u y [ ] 0 1 x 1 0 1 0 . 0 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = K = [ 1 0 ]

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 6.3极点配置问题 系统性能:稳态性能和动态性能 稳态性能:稳定性、静态误差 ·动态性能:调节时间、响应速度.. 影响系统稳定性、动态性能的因素: ·极点位置(系统矩阵的特征值) 通过反馈控制器的设计,可使得闭环系统的极点 位于预先给定的期望位置
系统性能:稳态性能和动态性能 • 稳态性能:稳定性、静态误差 • 动态性能:调节时间、响应速度... 影响系统稳定性、动态性能的因素: • 极点位置(系统矩阵的特征值) 通过反馈控制器的设计,可使得闭环系统的极点 位于预先给定的期望位置。 6.3 极点配置问题