
Shanghai Jiao Tong University 第四章经典控制理论与方法:频域方法 上海交通大学自动化系 Department of Automation Shanghai Jiao Tong University
Shanghai Jiao Tong University 第四章 经典控制理论与方法:频域方法

Shanghai Jiao Tong University 背景 ©时域分析法的缺点 ·高阶系统的分析难以进行 当系统某些元件的传递函数难以列写时,整个系统 的分析工作将无法进行 物理意义欠缺 频率响应法 © ·二十世纪三十年代发展起来 。 研究自动控制系统的一种工程方法 ·利用频率特性进行控制系统分析的图解方法 可方便地用于控制工程中的系统分析与设计
Shanghai Jiao Tong University 背景 时域分析法的缺点 • 高阶系统的分析难以进行 • 当系统某些元件的传递函数难以列写时,整个系统 的分析工作将无法进行 • 物理意义欠缺 频率响应法 • 二十世纪三十年代发展起来 • 研究自动控制系统的一种工程方法 • 利用频率特性进行控制系统分析的图解方法 • 可方便地用于控制工程中的系统分析与设计

Shanghai Jiao Tong University 内容 >控制系统的频域分析法 >频率特性 ·Bode图 •最小相位系统 ·性能分析
Shanghai Jiao Tong University 内容 ¾控制系统的频域分析法 ¾频率特性 • Bode图 • 最小相位系统 • 性能分析

Shanghai Jiao Tong University 1、频率特性 元 ©频率特性,又叫频率响应 ·控制系统在频域中的一种数学模型 ©系统频率特性能 ·间接地揭示系统的动态特性和稳态特性 ©频率响应法的优点 ·图解方法研究系统的稳定性 ·不必求解系统的特征根,形象直观和计算量少 。 频率特性可用实验方法测出,具有明确的物理意义 ·对于难以列写微分方程系统来说,具有重要的实际意义 o 可推广应用于某些非线性系统 ·例如含有延迟环节的系统 o 可方便设计出能有效抑制噪声的系统
Shanghai Jiao Tong University 1、频率特性 频率特性,又叫频率响应 • 控制系统在频域中的一种数学模型 系统频率特性能 • 间接地揭示系统的动态特性和稳态特性 频率响应法的优点 • 图解方法研究系统的稳定性 • 不必求解系统的特征根,形象直观和计算量少 • 频率特性可用实验方法测出,具有明确的物理意义 • 对于难以列写微分方程系统来说,具有重要的实际意义 • 可推广应用于某些非线性系统 • 例如含有延迟环节的系统 • 可方便设计出能有效抑制噪声的系统
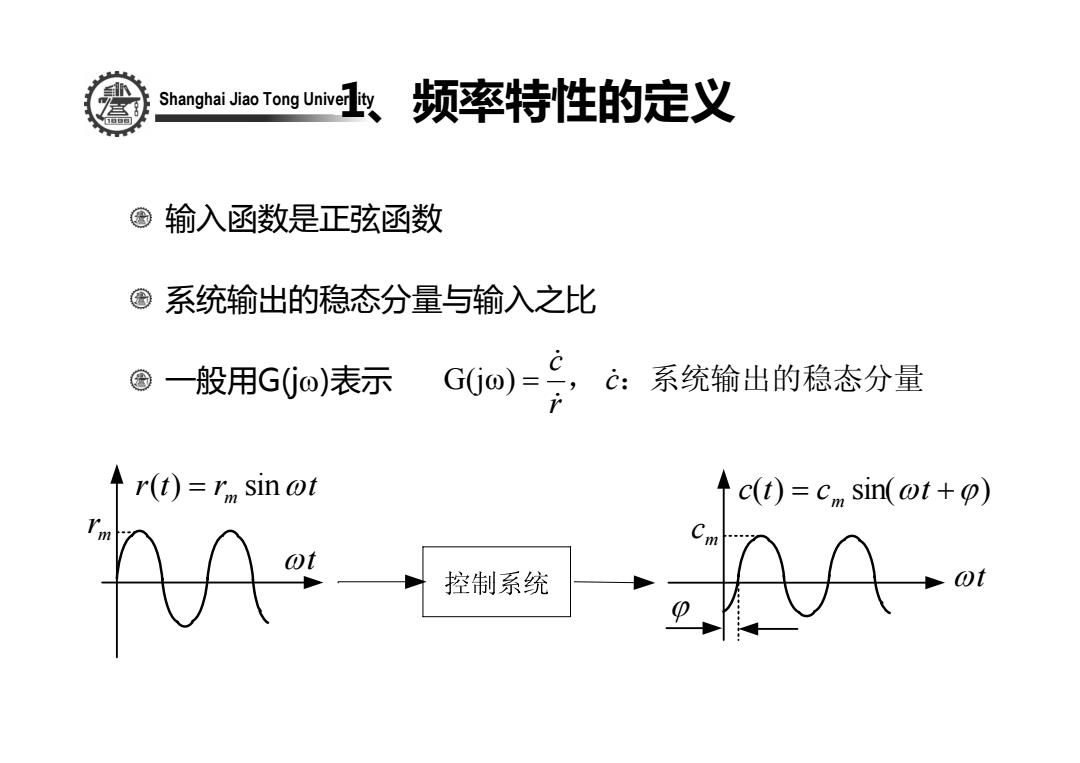
Shanghai Tong Unive?女频率特性的定义 ©输入函数是正弦函数 ©系统输出的稳态分量与输入之比 ©一般用G(jo)表示 G(o)=9,c 系统输出的稳态分量 ↑r(t)=r sin ot ↑c(t)=c sin(ot+p) 控制系统
Shanghai Jiao Tong University 1、频率特性的定义 输入函数是正弦函数 系统输出的稳态分量与输入之比 一般用G(jω)表示 r t r t ( ) = m sinω ωt mr c(t) = c sin(ωt +ϕ) m ωt mc ϕ , c:系统输出的稳态分量 r c & & & G(jω) =

Shanghai Jia Tong Univerity 频率特性的性质 ©频率特性是一种描述系统内在特性的数学模型 ·与传递函数类似,当系统结构参数给定,频率特性也完全确定 。 与外界因素无关 ©系统的稳态输出与输入具有相同的角频率0 。 系统中的储能元件引起的 ·输出与输入幅值之比A(o)是o的函数 ·输出与输入相位移(o)是o的函数 国 频率特性反应了系统性能 ·根据频率特性,可以确定系统的性能指标 ·不同的性能指标,对系统的频率特性提出不同的要求 ©多数实际系统具有低通滤波器的特性 。 即当o→o,幅值比A(o)多趋于0 ©频率特性仅适用于线性元件或系统
Shanghai Jiao Tong University 1、频率特性的性质 频率特性是一种描述系统内在特性的数学模型 • 与传递函数类似,当系统结构参数给定,频率特性也完全确定 • 与外界因素无关 系统的稳态输出与输入具有相同的角频率ω • 系统中的储能元件引起的 • 输出与输入幅值之比A(ω)是ω的函数 • 输出与输入相位移ϕ(ω)是ω的函数 频率特性反应了系统性能 • 根据频率特性,可以确定系统的性能指标 • 不同的性能指标,对系统的频率特性提出不同的要求 多数实际系统具有低通滤波器的特性 • 即当ω→∞,幅值比A(ω)多趋于0 频率特性仅适用于线性元件或系统

Shanghai Jiao Tong Univer ity 频率特性的求取 ©根据定义求取 ·对已知系统的微分方程,把正弦输入函数代入,求其稳态解 ·取输出稳态分量与输入正弦量的复数比即可得到 ©实验法:通过实验的方法直接测得 ©解析法:根据传递函数求取 ·用s=jo代入系统的传递函数 G(s)= C(s)bmsm+bm-ism++bs+bo R(s) ans+an-is-+......+as+ao →Gio)= C(j@)_bm(j@)m+bm-(j@)m+......+bj(j@)+bo R(j@) a(j@)"+a-(jo)+....+a (jo)+ao =A(@)ei()=U(@)+jV(@)
Shanghai Jiao Tong University 1、频率特性的求取 根据定义求取 • 对已知系统的微分方程,把正弦输入函数代入,求其稳态解 • 取输出稳态分量与输入正弦量的复数比即可得到 实验法:通过实验的方法直接测得 解析法:根据传递函数求取 • 用s=jω代入系统的传递函数 A( )e U( ) jV( ) a (j ) a (j ) a (j ) a b (j ) b (j ) b (j ) b R(j ) C(j ) G(j ) a a a a b b b b R(s) C(s) G(s) j ( ) 1 0 n 1 n 1 n n 1 0 m 1 m 1 m m 1 0 n 1 n 1 n n 1 0 m 1 m 1 m m ω ω ω ω ω ω ω ω ω ω ω ω ϕ ω = = + + + + + + + + + ⇒ = = + + + + + + + + = = − − − − − − − − LL LL LL LL s s s s s s

Shaghai iTonverit频率特性的表示方法 解析形式 C(jo) G(joH(j@)= R(j@) 幅频/相频形式 -G(jo)H(j@)ZG(j@)H(j@) ·指数形式 =A(@)ei() 。 实频/虚频形式 =U(o)+iv(@) ·三角函数形式 =A(@)cos(@)+jA(@)sin(@) ©图解形式 jv G(jo) ·Nyquist图 ·Bode图 V(0) ·对数频率特性图 A(0) · 对数幅相频特性图 P(@) 0 U(@)U
Shanghai Jiao Tong University 1、频率特性的表示方法 解析形式 • 幅频/相频形式 • 指数形式 • 实频/虚频形式 • 三角函数形式 图解形式 • Nyquist图 • Bode图 • 对数频率特性图 • 对数幅相频特性图 ( ) cos ( ) ( )sin ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ω ϕ ω ω ϕ ω ω ω ω ω ω ω ω ω ω ω ω ϕ ω A jA U jV A e G j H j G j H j R j C j G j H j j = + = + = = ∠ = jV V ( ) ω A ( ) ω U ( ) ω ϕ ( ) ω G j ( ) ω 0 U

Shanghai Jiao Tong University 内容 >控制系统的频域分析法 >频率特性 ·Bode图 •最小相位系统 ·性能分析
Shanghai Jiao Tong University 内容 ¾控制系统的频域分析法 ¾频率特性 • Bode图 • 最小相位系统 • 性能分析
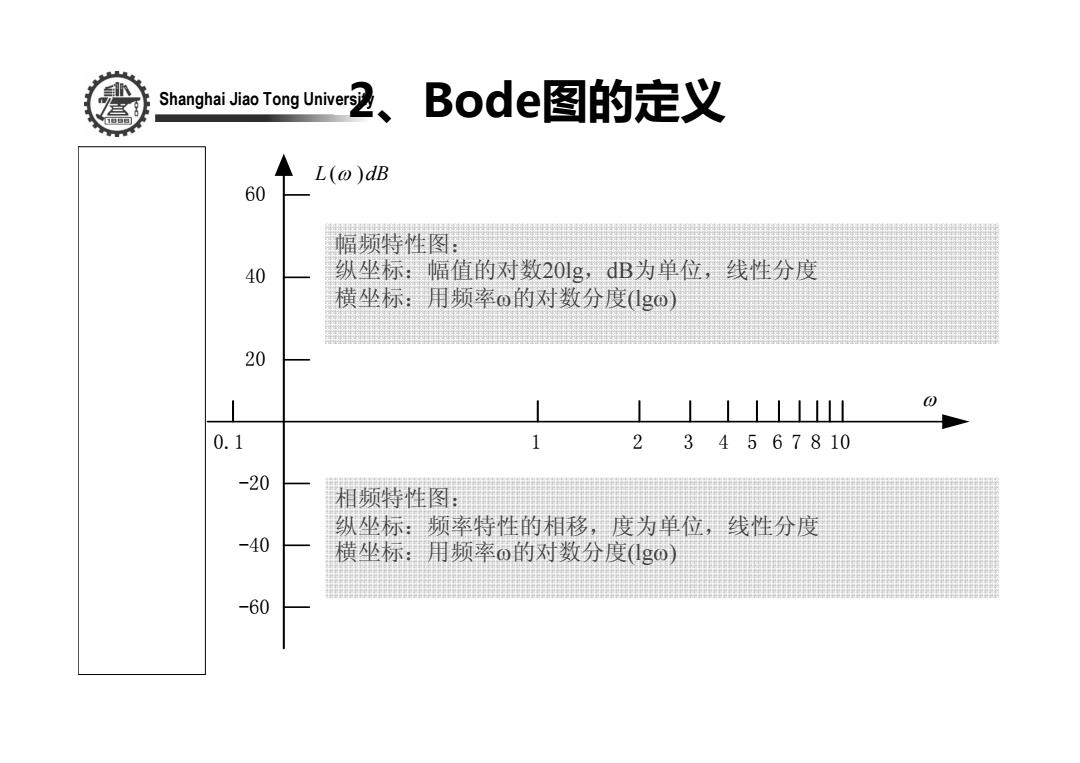
Shanghai Tong Univer2、BOde图的定义 L(@)dB 60 幅频特性图: 40 纵坐标:幅值的对数20lg,dB为单位,线性分度 横坐标:用频率o的对数分度go) 20 L⊥LLL山 0.1 1 234567810 -20 相频特性图: 纵坐标:频率特性的相移,度为单位,线性分度 -40 横坐标:用频率o的对数分度(go) -60
Shanghai Jiao Tong University o − 180 0.1 1 10 20 40 60 -20 -40 -60 o 0 o 90 o 180 o − 90 2 34 6 8 5 7 ω ϕ (ω ) L (ω )dB 2、Bode图的定义 幅频特性图: 纵坐标:幅值的对数20lg,dB为单位,线性分度 横坐标:用频率ω的对数分度(lgω) 相频特性图: 纵坐标:频率特性的相移,度为单位,线性分度 横坐标:用频率ω的对数分度(lgω)