
Shanghai Jiao Tong University 《经典控制理论》:时域分析
Shanghai Jiao Tong University 《经典控制理论》:时域分析 《经典控制理论》:时域分析

Shanghai Jiao Tong University 系统的性能 输出:C()=Cts()+Css() © 系统的动态特性:Cts(t) lim cis(t)=0 t→00 ·系统达到稳态所需时间 过渡期间输出偏离输入的程度 @ 系统的稳态特性:Css(t) ·输入信号只影响稳态部分(线性系统 ) 稳态误差:系统达到稳态后输出与输入的偏差 ©系统的稳定性 ·稳定是系统正常运行的前提 ·控制理论研究的重要课题
Shanghai Jiao Tong University 系统的性能 输出:c(t) = cts(t) + css(t) 系统的动态特性: cts(t) • 系统达到稳态所需时间 • 过渡期间输出偏离输入的程度 系统的稳态特性: css(t) • 输入信号只影响稳态部分(线性系统) • 稳态误差:系统达到稳态后输出与输入的偏差 系统的稳定性 • 稳定是系统正常运行的前提 • 控制理论研究的重要课题 lim ( ) 0 ts t c t →∞ =

Shanghai Jiao Tong University 内容 >控制系统的时域分析法 >稳定性 ·稳态性能 ·动态性能
Shanghai Jiao Tong University 内容 ¾控制系统的时域分析法 ¾稳定性 • 稳态性能 • 动态性能

1.稳定的充要条件 Shanghai Jiao Tong University ④闭环传递函数:中(S) Φ(s)= C(s)_bns"+bnm-sm-+…+bs+b= B(s) R(s) anS”+an-1s-+…+as+a0 D(s) 。m≤n ·C(S:输出信号拉氏变换 R(S:输入信号拉氏变换 ·D(S)=0:特征方程 ·pi(i=1,,n):特征方程的根
Shanghai Jiao Tong University 1. 稳定的充要条件 1. 稳定的充要条件 ( ) ( ) ( ) ( ) ( ) 1 0 1 1 1 0 1 1 D s B s a s a s a s a b s b s b s b R s C s s n n n n m m m m = + + + + + + + + Φ = = − − − − L L

Shanghai Jiao Tong University 1、稳定的充要条件 ©线性系统稳定的充要条件 ·闭环系统特征方程的所有根均具有负实部 ·或者说,闭环传递函数的极点均分布在平面的左半部 ©性质 ·稳定性仅取决于系统自身的固有特性,而与外界条件无关 ·稳定系统的脉冲响应随t→0,必趋于零,不稳定系统趋于0 稳定系统在幅值有界的输入信号下,输出也必幅值有界 特征根 s3+4s2+5s+2=0 C(s) 1 R(S)s3+4s2+5s+2 → (s+1)(s2+3s+2)=(s+1)2(s+2)=0 4-8-8,是条名 闭环系
Shanghai Jiao Tong University 1. 稳定的充要条件 1. 稳定的充要条件 线性系统稳定的充要条件 • 闭环系统特征方程的所有根均具有负实部 • 或者说,闭环传递函数的极点均分布在平面的左半部 性质 • 稳定性仅取决于系统自身的固有特性,而与外界条件无关 • 稳定系统的脉冲响应随t→∞,必趋于零,不稳定系统趋于∞ • 稳定系统在幅值有界的输入信号下,输出也必幅值有界 4 5 2 1 R(s) C(s) 3 2 + + + = s s s 1, 1, 2 ( 1)( 3 2) ( 1) ( 2) 0 s 4 5 2 0 1 2 3 2 2 3 2 = − = − = − + + + = + + = + + + = s s s s s s s s 特征根 s s 闭环系 统稳定

1.稳定性判别方法 Shanghai Jiao Tong University 直接求根 解微分方程:方程阶次较高时难以应用 。 根轨迹法(图解求根) ·绘制闭环极点随开环某参数变化的轨迹 ·利用计算机数值解或符号解 ©求特征根的范围 ·劳斯判据:根据特征方程系数判定(代数方法) Nyquist判据和Bode图(半图解法) ·根据开环频率特性判断闭环系统的稳定性 ·由于频率特性曲线易由实验获取,故该方法较实用 ©李雅普诺夫判据:用于非线性、任意阶系统 ©波波夫法:用于研究非线性鲁里叶型的时变系统 ©相平面法:多用于一、二阶非线性系统
Shanghai Jiao Tong University 1. 稳定性判别方法 1. 稳定性判别方法 直接求根 • 解微分方程:方程阶次较高时难以应用 • 根轨迹法(图解求根) • 绘制闭环极点随开环某参数变化的轨迹 • 利用计算机数值解或符号解 求特征根的范围 • 劳斯判据:根据特征方程系数判定(代数方法) • Nyquist判据和Bode图(半图解法) • 根据开环频率特性判断闭环系统的稳定性 • 由于频率特性曲线易由实验获取,故该方法较实用 李雅普诺夫判据:用于非线性、任意阶系统 波波夫法:用于研究非线性鲁里叶型的时变系统 相平面法:多用于一、二阶非线性系统

Shanghai Jiao Tong University 1.劳斯判据 系统稳定性 ·取决于特征根的分布 ·根是由闭环系统特征方程的系数决定的 ©劳斯(Routh)稳定判据 ·由特征方程的系数来分析系统的稳定性的一种代数判据 ©所有根均分布在左半平面的必要条件 ·设线性系统的特征方程为: ansn an-isn-1 +......as1 +ao=0 ·方程所有系数均为正数 ·若特征方程中任一系数为负或缺项(系数为零),则系统不稳定 ©适用条件 ·系统的特征方程为代数方程,且所有系数为实数
Shanghai Jiao Tong University 1. 劳斯判据 1. 劳斯判据 系统稳定性 • 取决于特征根的分布 • 根是由闭环系统特征方程的系数决定的 劳斯 (Routh) 稳定判据 • 由特征方程的系数来分析系统的稳定性的一种代数判据 所有根均分布在左半平面的必要条件 • 设线性系统的特征方程为: ansn + an-1sn-1 + …… + a1s1 + a0 = 0 • 方程所有系数均为正数 • 若特征方程中任一系数为负或缺项(系数为零),则系统不稳定 适用条件 • 系统的特征方程为代数方程,且所有系数为实数

Shanghai Tong Unversity1、劳斯判据:例 -0.77±0.9i 5s4+3s3+4s2+6=0 0.47±0.8i 5s4+4s3-2s2+3+5=0 -1±0.4i 0.6t0.68i 534+4s3+252+s+5=0 -0.87±0.7i 0.47±0.76i
Shanghai Jiao Tong University1. 劳斯判据:例 1. 劳斯判据:例 5 3 4 6 0 4 3 2 s + s + s + = 5 4 2 5 0 4 3 2 s + s − s + s + = 5 4 2 5 0 4 3 2 s + s + s + s + = ‐0.77 ± 0.9i 0.47 ± 0.8i ‐1 ± 0.4i 0.6 ± 0.68i ‐0.87 ± 0.7i 0.47 ± 0.76i

Shanghai J Tong University】、j 劳斯判据步骤 将特征方程式的系数 80 an-2 an-4 an-6… 按下列规则排成两行 an-3 an-5 an-7… b b, b3 ©建立劳斯表 Sh-3 C2 4…0444 ·又叫劳斯阵列 ©根据劳斯判据判别 b=da-idn-2-andn=3 b2=a-1-4-a,a-s 系统的稳定性 an- an- 表中第一列各值为正, b3=a1-14m-6-0,4n-7 则系统稳定; an-1 ·若劳斯表中第一列出 C1= ban-3-anb2 C,=bidr-s-drby 现负值,则系统不稳定 b b 实部为正的根的数目,等于表中第一列系数符号改变的次数
Shanghai Jiao Tong University1. 劳斯判据步骤 1. 劳斯判据步骤 将特征方程式的系数 按下列规则排成两行 建立劳斯表 • 又叫劳斯阵列 根据劳斯判据判别 系统的稳定性 • 表中第一列各值为正, 则系统稳定; • 若劳斯表中第一列出 现负值,则系统不稳定 • 实部为正的根的数目,等于表中第一列系数符号改变的次数 c c b b b ...... ...... s c c ...... s b b b ....... s a a a a ...... s a a a a ...... 1 1 5 1 3 2 1 1 3 1 2 1 1 1 6 7 3 1 1 4 5 2 1 1 2 3 1 1 2 n-3 1 2 3 n-2 n-1 n-3 n-5 n-7 n-1 n n-2 n-4 n-6 n b b a a b b b a a b a a a a a a a a a a a a a a a n n n n n n n n n n n n n n n n n n n − − − − − − − − − − − − − − − − − = − = − = − = − =
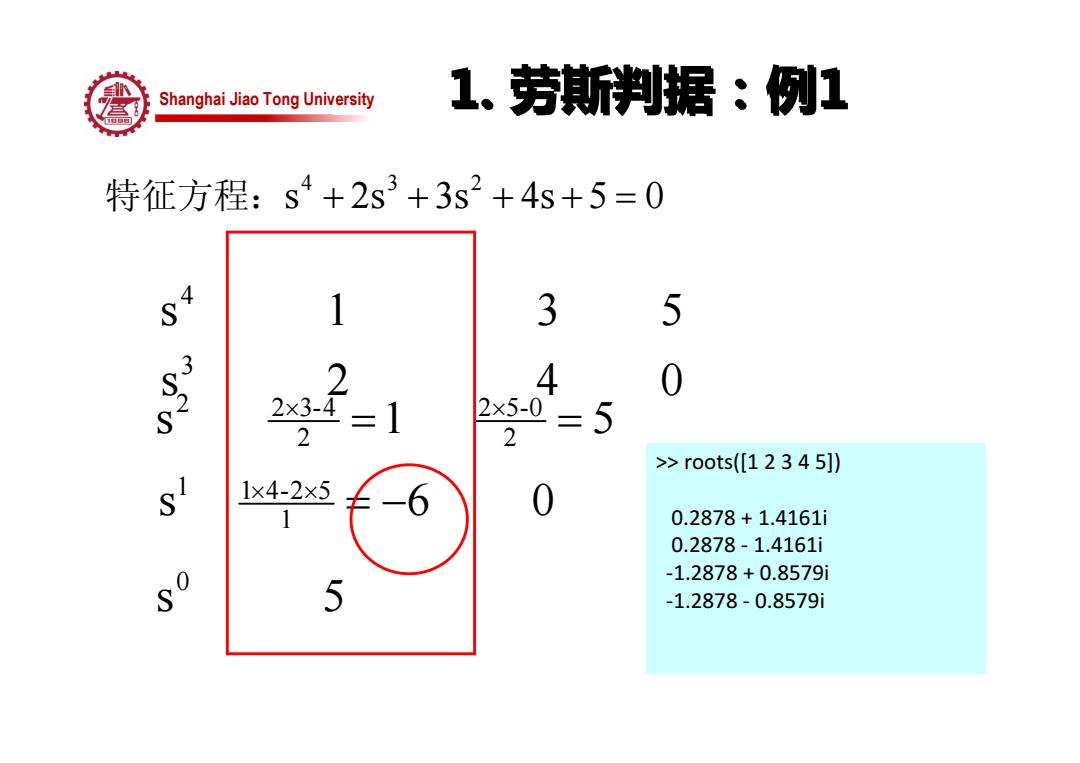
Shanghai Jiao Tong University 1.劳斯判据:例1 特征方程:S4+2s3+3s2+4s+5=0 1 3 5 23-=1 2 4 0 2×5-0 二 2 5 2 >>roots([12345]) s 1x4-2x5 1 0.2878+1.4161i 0.2878-1.4161i -1.2878+0.8579i 5 -1.2878-0.8579i
Shanghai Jiao Tong University 1. 劳斯判据:例1 1. 劳斯判据:例1 s 2s 3s 4s 5 0 4 3 2 + + + + = s 1 5 2 2 5-0 2 2 2 3-4 = = × × s 6 0 1 1 1 4-2 5 = − × × s 5 0 s 2 4 0 s 1 3 5 3 4 >> roots([1 2 3 4 5]) 0.2878 + 1.4161i 0.2878 ‐ 1.4161i ‐1.2878 + 0.8579i ‐1.2878 ‐ 0.8579i 特征方程: