
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 第五章系统稳定性 5.1稳定性的经典定义 实际系统正常工作的前提是系统必须是稳定的 系统稳定性有几种不同的定义 稳定性经典定义:对系统闭环传递函数定义的稳定性,是有 界输入有界输出稳定性(BIBO稳定性) 定义5.1.1老虑线性系统,如果由有界给定值输入所产生 的系统输出也是有界的,则称系统是BIB0稳定的
第五章 系统稳定性 5.1 稳定性的经典定义 实际系统正常工作的前提是系统必须是稳定的 系统稳定性有几种不同的定义 稳定性经典定义:对系统闭环传递函数定义的稳定性,是有 界输入有界输出稳定性(BIBO稳定性 ) 定义5.1.1 考虑线性系统,如果由有界给定值输入所产生 的系统输出也是有界的, 则称系统是BIBO稳定的

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 定理5.1.1单变量线性系统的BIB0稳定的充分必要条件是 所有闭环极点都具有负实部 例5.1.1设闭环系统的状态空间描述为 -10 1 x- x+ 0 2.5 0 y=[1 1] 其传递函数为 8(s)=c(SI-A)b= (s-2.5)1 (s+1)(s-2.5)(s+1) 所以系统是BIB0稳定的
定理5.1.1 单变量线性系统的BIBO稳定的充分必要条件是 所有闭环极点都具有负实部 例5.1.1 设闭环系统的状态空间描述为 [ ] x x x 1 1 0 1 0 2.5 1 0 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ + ⎦ ⎤ ⎢ ⎣ ⎡ − = y & u 其传递函数为 ( 1 ) 1 ( 1)( 2.5 ) ( 2.5 ) ( ) ( ) 1 + = + − − = − = − s s s s g s c sI A b 所以系统是BIBO稳定的

上濟究通大学 SHANGHAI JIAO TONG UNIVERSITY 5.2内部稳定性 稳定性一输出稳定,也就是当系统在干扰取消后,在一定时 间内,其输出会恢复到原来的稳态输出 内部稳定性一针对系统内部状态,反映的是系统内部状态受 干扰信号的影响。当扰动信号取消后,系统的内部状态会在 一定时间内恢复到原来的平衡状态,则称系统内稳定 定义5.2.1考虑线性系统,如果在系统任何一点有界输入 在其他点所产生的输出都是有界的,则称系统是内稳定的
5.2 内部稳定性 稳定性-输出稳定,也就是当系统在干扰取消后,在一定时 间内,其输出会恢复到原来的稳态输出 定义5.2.1 考虑线性系统,如果在系统任何一点有界输入 在其他点所产生的输出都是有界的,则称系统是内稳定的 内部稳定性-针对系统内部状态,反映的是系统内部状态受 干扰信号的影响。当扰动信号取消后,系统的内部状态会在 一定时间内恢复到原来的平衡状态,则称系统内稳定
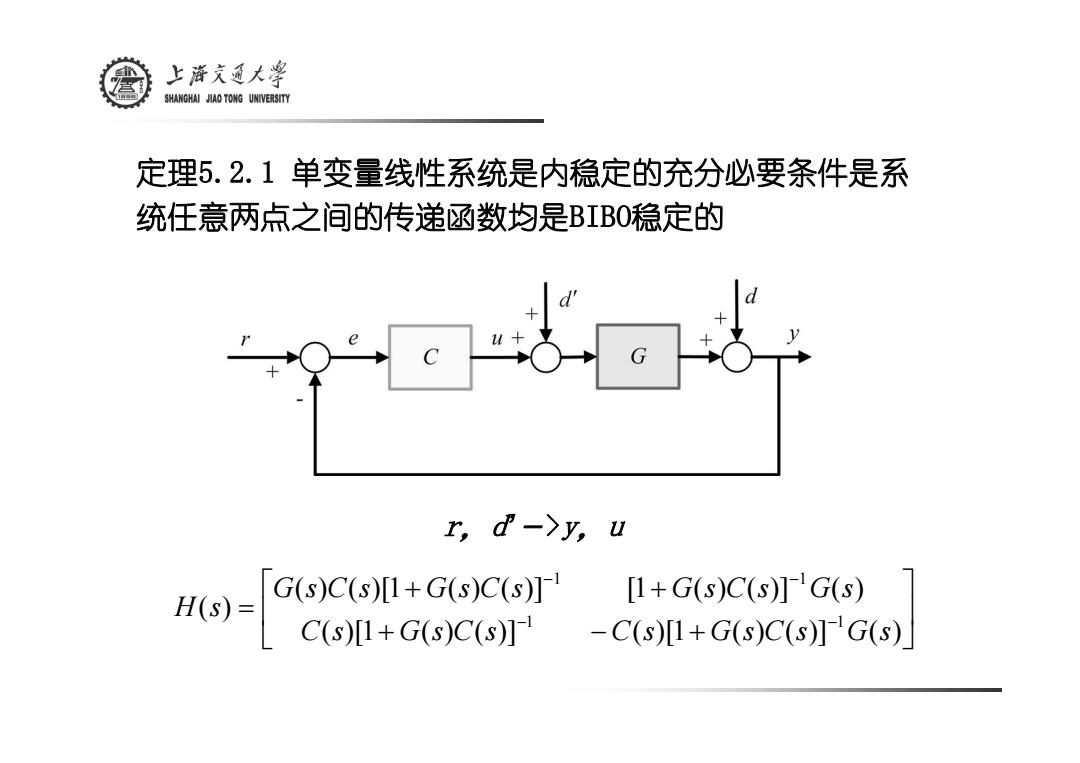
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 定理5.2.1单变量线性系统是内稳定的充分必要条件是系 统任意两点之间的传递函数均是BIBO稳定的 r,d->y,u H(S)= G(s)C(s)[1+G(s)C(s)]1 [1+G(s)C(s)]G(s) C(s)[I+G(s)C(s)】 -C(s)1+G(s)C(s)1G(s)
定理5.2.1 单变量线性系统是内稳定的充分必要条件是系 统任意两点之间的传递函数均是BIBO稳定的 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − + + + = − − − − ( )[ 1 ( ) ( )] ( )[ 1 ( ) ( )] ( ) ( ) ( )[ 1 ( ) ( )] [ 1 ( ) ( )] ( ) ( ) 1 1 1 1 C s G s C s C s G s C s G s G s C s G s C s G s C s G s H s r,d’ - >y,u
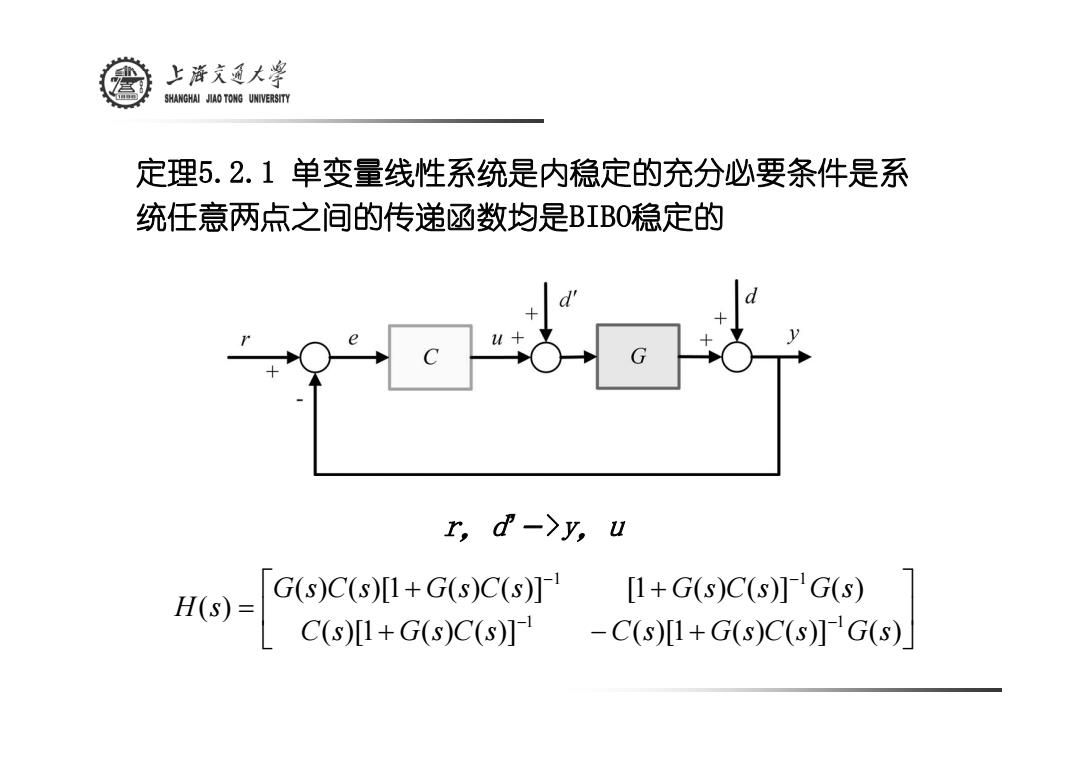
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 定理5.2.1单变量线性系统是内稳定的充分必要条件是系 统任意两点之间的传递函数均是BIBO稳定的 r,d->y,u H(S)= G(s)C(s)[1+G(s)C(s)]1 [1+G(s)C(s)]G(s) C(s)[I+G(s)C(s)】 -C(s)1+G(s)C(s)1G(s)
定理5.2.1 单变量线性系统是内稳定的充分必要条件是系 统任意两点之间的传递函数均是BIBO稳定的 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − + + + = − − − − ( )[ 1 ( ) ( )] ( )[ 1 ( ) ( )] ( ) ( ) ( )[ 1 ( ) ( )] [ 1 ( ) ( )] ( ) ( ) 1 1 1 1 C s G s C s C s G s C s G s G s C s G s C s G s C s G s H s r,d’ - >y,u

上誉文廷大¥ SHANGHAI JIAO TONG UNIVERSITY 作业4单变量线性系统如下: -1 C(s)=5 、 1 G(S) S+1 (s+1)(s-1) 试分析其稳定性和内部稳定性
作业4 单变量线性系统如下: 1 1 ( ) + − = s s C s ( 1)( 1 ) 1 ( ) + − = s s G s 试分析其稳定性和内部稳定性

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 5.3李雅普诺夫稳定性 定义:如果对于给定的任意实数£>0,都对应地存在另一 实数δ>0,使系统满足 |x0-x≤6 的任一初始状态x,的响应都满足 x0)-xe≤& t≥to 则平衡状态x是李雅普诺夫意义上稳定的
定义: 如果对于给定的任意实数 ,都对应地存在另一 实数 ,使系统满足 ε > 0 δ > 0 x 0 − x e ≤ δ 的任一初始状态 的响应都满足 x 0 − ≤ ε e x(t) x 0 t ≥ t 则平衡状态 是李雅普诺夫意义上稳定的 x e 5.3 李雅普诺夫稳定性

上文大学 SHANGHAI JIAO TONG UNIVERSITY 稳定性定义的平面几何表示 设系统初始状态x,位于平衡状态x。为球心、半径为δ的 闭球域内,如果系统稳定,则状态方程的解在在t>t0的所有 时间内,都位于以xe为球心,半径为ε的闭球域内 S(E) S(e) S(e) S(5) S(5) (a)李推普诺夫意义下的稳定性 ()渐近稳定性 (c)不稳定性
稳定性定义的平面几何表示 设系统初始状态 x0 位于平衡状态 x e 为球心、半径为δ的 闭球域内,如果系统稳定,则状态方程的解在在t≥t0的所有 时间内,都位于以 xe 为球心,半径为ε的闭球域内 (a)李雅普诺夫意义下的稳定性 (b)渐近稳定性 (c)不稳定性

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 李亚普诺夫判定方法 如果/(x)>0,则称其是正定的 基本思路: 定义一个虚构的正定标量能量函数V(x),根据(x)的符号性 质,可以判断系统的状态稳定性 能量函数称为李亚普诺夫函数 物理原理:若系统贮存的能量随时间推移而衰减,系统迟早 会到达平衡状态 假设:系统的状态方程为x=f(x,t),xe=0为平衡状态,即 元。=f0,t)=0
李亚普诺夫判定方法 基本思路: 定义一个虚构的正定标量能量函数 ,根据 的符号性 质,可以判断系统的状态稳定性 V(x) V(x) & 能量函数称为李亚普诺夫函数 如果 ,则称其是正定的 V(x) > 0 物理原理:若系统贮存的能量随时间推移而衰减,系统迟早 会到达平衡状态 假设:系统的状态方程为 xe=0为平衡状态,即 x& = f (x,t), x & e = f (0,t) = 0

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 李亚普诺夫稳定性定理: 如果在xe某一邻域内,存在一标量函数V(x)满足以下条件: 1)V(x)是正定的, 正定矩阵:各主 2)(x)是负定的, 子式均大于零 则系统在原点处的平衡状态是渐进稳定的 定理5.3.1线性定常系统x=Ax的零平衡状态xe=0为 渐进稳定的充要条件是:对任意给定正定实对称阵Q,如下 李亚普诺夫方程 AP+PA=-O 存在唯一的正定的对称解P 常取Q-1
李亚普诺夫稳定性定理: 如果在xe某一邻域内,存在一标量函数 满足以下条件: 1) 是正定的, 2) 是负定的, V ( x ) & V ( x ) V ( x ) 则系统在原点处的平衡状态是渐进稳定的 定理5.3.1 线性定常系统 的零平衡状态xe=0为 渐进稳定的充要条件是:对任意给定正定实对称阵 Q,如下 李亚普诺夫方程 存在唯一的正定的对称解P A P PA Q T + = − 正定矩阵:各主 子式均大于零 x& = Ax 常取 Q = I V x Px T =