
第四章 线性控制系统的能控性和能观性
1 第四章 线性控制系统的能控性和能观性

基本概念 。能控性和能观性是表征系统结构特性的两个重要 概念 。能控性和能观性的概念,对系统的控制和状态估 计问题的研究有重要意义 。粗略地讲,能控性分析系统状态能否被输入控制 ,而能观性分析系统初始状态能否从对系统输出 的观测来得到
2 基本概念 能控性和能观性是表征系统结构特性的两个重要 概念 能控性和能观性的概念,对系统的控制和状态估 计问题的研究有重要意义 粗略地讲,能控性分析系统状态能否被输入控制 ,而能观性分析系统初始状态能否从对系统输出 的观测来得到。���
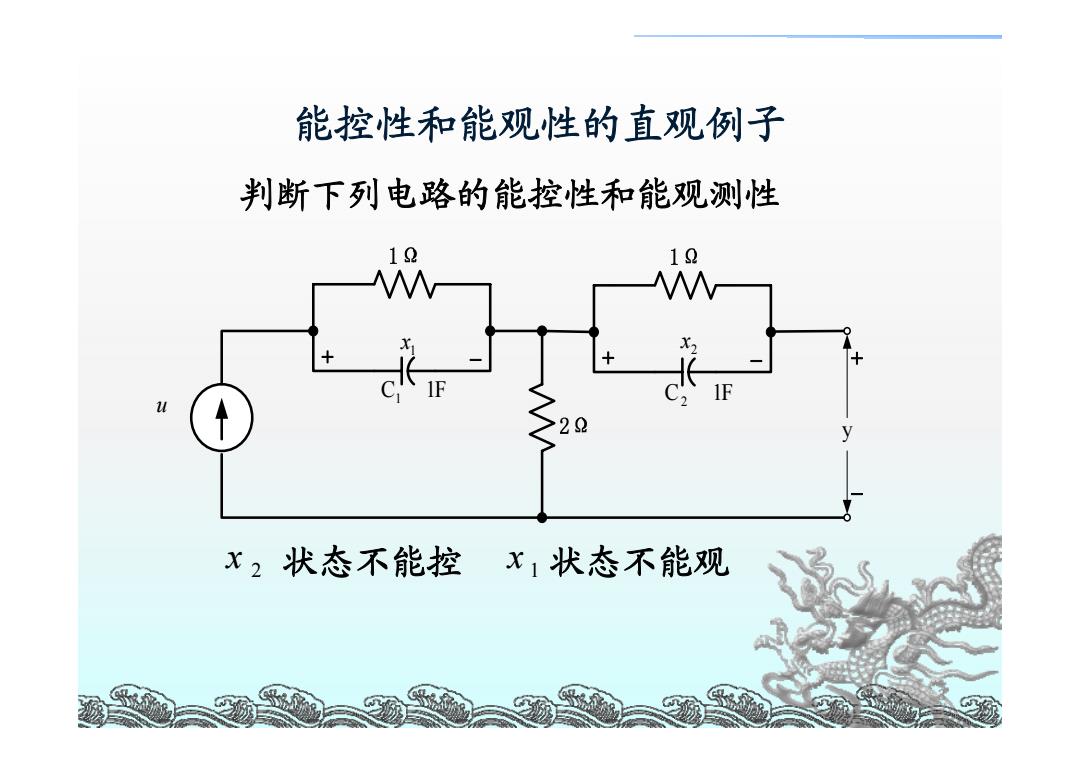
能控性和能观性的直观例子 判断下列电路的能控性和能观测性 12 10 22 y x2状态不能控 x1状态不能观
3 能控性和能观性的直观例子 u 1 x + − C1 1F 2 x + − C2 1F + − y x 2 状态不能控 1 x 状态不能观 判断下列电路的能控性和能观测性

本章主要内容 4.1线性定常系统的能控性 4.2线性定常系统的能观性 4.3线性时变系统的能控性和能观性 4.4离散时间系统的能控性和能观性 4.5能控性与能观性的对偶关系 4.6能控标准型和能观标准型 4.7线性系统的结构分解
4 本章主要内容 4.1 线性定常系统的能控性 4.2 线性定常系统的能观性 4.3 线性时变系统的能控性和能观性 4.4 离散时间系统的能控性和能观性 4.5 能控性与能观性的对偶关系 4.6 能控标准型和能观标准型 4.7 线性系统的结构分解

4.1线性定常系统的能控性 。能控性是系统在控制作用ū(t)的控制下, 系统状态向量x(t)的转移能力 。能控性和输出y(t)无关,只需从系统的状 态方程出发研究系统的能控性
5 4.1 线性定常系统的能控性 能控性是系统在控制作用u(t)的控制下, 系统状态向量x(t)的转移能力 能控性和输出y(t)无关,只需从系统的状 态方程出发研究系统的能控性��

4.1.1能控性定义 定义4-1[能控性]线性连续定常系统的状态方程 x=Ax+Bu (4-1) 如果对任意初始状态x()=x,和任意终端状态()=x 存在一个无约束容许输入(t),能在有限时间区间[,4] 内,使系统状态由飞,转移到X,则称此系统或(A,B)对 是状态完全能控的,或简称此系统或(A,B)对是能控的。 否则,则称此系统或(A,B)对是状态不完全能控的,或 简称不能控。 说明: •对状态转移的轨迹没有规定,表征了能控性的定性特点 •无约束容许输入是指的每个分量的幅值没有加以限 制,但W的每个分量均需在时间区间[to,4]上平方可积
6 4.1.1 能控性定义 定义4-1[能控性]线性连续定常系统的状态方程 (4 —1) 如果对任意初始状态 和任意终端状态 , 存在一个无约束容许输入 ,能在有限时间区间 内,使系统状态由 转移到 ,则称此系统或 对 是状态完全能控的,或简称此系统或 对是能控的。 否则,则称此系统或 对是状态不完全能控的,或 简称不能控。 说明: •对状态转移的轨迹没有规定,表征了能控性的定性特点 •无约束容许输入是指 的每个分量的幅值没有加以限 制,但 的每个分量均需在时间区间 上平方可积 x& = Ax Bu + 0 0 x x ( ) t = 1 x x ( ) = f t u( )t [ , ] 0 1 t t 0 x x f ( ) A,B ( ) A,B ( ) A,B u u [ , ] 0 1 t t
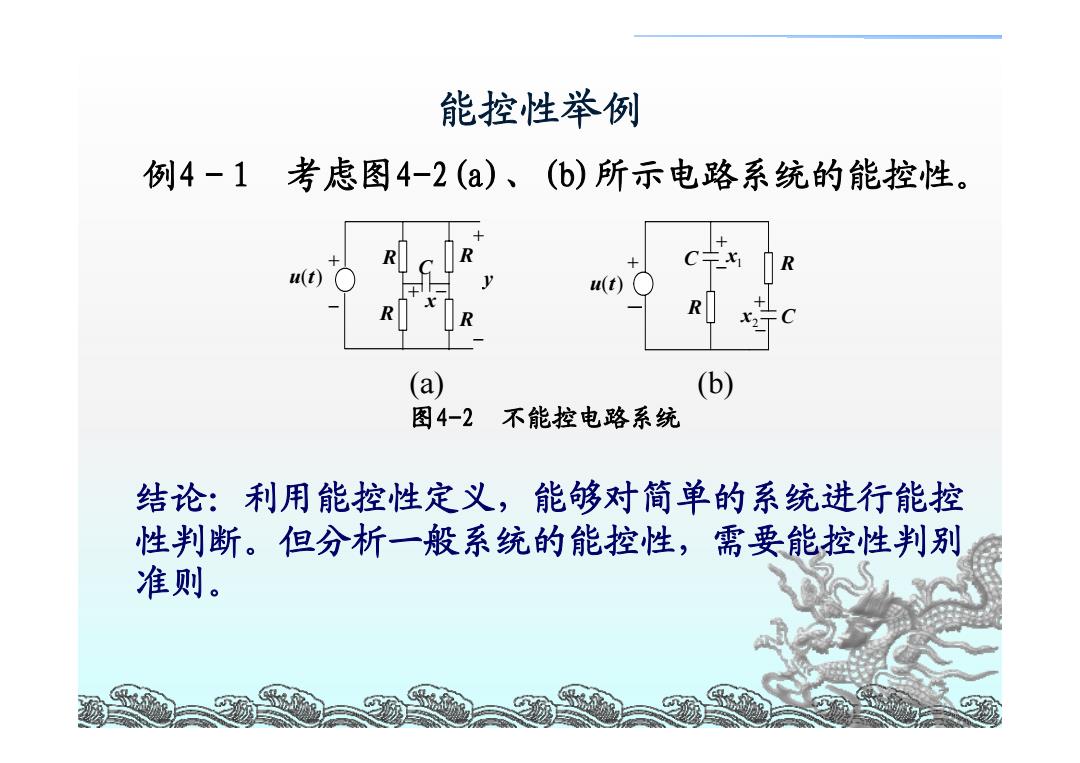
能控性举例 例4-1考虑图4-2(a)、(b)所示电路系统的能控性。 u(t) u(t) (a) (b) 图4-2 不能控电路系统 结论:利用能控性定义,能够对简单的系统进行能控 性判断。但分析一般系统的能控性,需要能控性判别 准则
7 能控性举例 例4-1 考虑图4-2(a)、(b)所示电路系统的能控性。 u(t) + − R R R + − C x y C C R R u(t) + + − − 1 x 2 x + − R + − (a) (b) 图4-2 不能控电路系统 结论:利用能控性定义,能够对简单的系统进行能控 性判断。但分析一般系统的能控性,需要能控性判别 准则

4.1.2线性定常系统的能控性判据 1、线性定常系统的能控性判据 定理4-1[能控性格拉姆矩阵判据]线性连续定常系统 x=Ax+Bu 为完全能控的充分必要条件是,存在时刻>0,使 如下定义的格拉姆矩阵 W(0,t)=∫eBB'e"d (4一3) 为非奇异 证明:见教材P112 格拉姆矩阵判据主要用于理论分析和推导
8 4.1.2 线性定常系统的能控性判据 定理4-1[能控性格拉姆矩阵判据]线性连续定常系统 为完全能控的充分必要条件是,存在时刻 ,使 如下定义的格拉姆矩阵 (4 —3) 为非奇异。 x& = Ax Bu + 0 t1 > 1 1 0 (0, ) A A W BB t T t Tt c t e e dt = ∫ 证明:见教材 P112 格拉姆矩阵判据主要用于理论分析和推导 1、线性定常系统的能控性判据

定理4-2[能控性秩判据]线性连续定常系统 x=Ax+Bu 为完全能控的充分必要条件为 rank[B AB…A"-B]=n (4—13) 式中,n为矩阵A的维数。 U=[B AB ..A"-B] (4—14) 称为系统的能控性判别矩阵。 证明:见教材P113 秩判据在线性定常系统的能控性判别中被经常应用 式(4一13)等价于矩阵U行满秩
9 定理4-2[能控性秩判据]线性连续定常系统 为完全能控的充分必要条件为 (4 —13) 式中,n为矩阵 A的维数。 (4 —14) 称为系统的能控性判别矩阵。 x Ax Bu & = + 1 [ ] B AB A Bn rank n − L = 1 U B AB A B [ ] n − = L 证明:见教材 P113 秩判据在线性定常系统的能控性判别中被经常应用 式 (4—13 )等价于矩阵 行满秩。 U

推论: (1)对于单输入系统,能控性判别矩阵为方阵,则有 (A,b)能控台U非奇异←台detU≠0 dtU的值表示了系统能控的程度,即能控度。 detU的值大表示系统远离不能控,即能控度大。 能控度的有物理意义为当通过状态反馈移动极,点位置时, 同样的移动距离,能控度越大,所需反馈增益越小,反 之,所需反馈增益越大。 对于多输入系统有类似的关系和性质。 (2)对于多输入系统,U阵非方,U严U为方阵,则有 (A,B)能控→UTU非奇异 则能控度即为detU'U的值
10 推论: (1)对于单输入系统,能控性判别矩阵为方阵,则有 能控 非奇异 的值表示了系统能控的程度,即能控度。 的值大表示系统远离不能控,即能控度大。 能控度的有物理意义为当通过状态反馈移动极点位置时, 同样的移动距离,能控度越大,所需反馈增益越小,反 之,所需反馈增益越大。 对于多输入系统有类似的关系和性质。 (2)对于多输入系统, 阵非方, 为方阵,则有 能控 非奇异 则能控度即为 的值。 ( ,) A b ⇔ U ⇔ det 0 U ≠ detU detU T U U U (,) A B T ⇔U U det T U U