
上游究通大学 SHANGHAI JIAO TONG UNIVERSITY 第三章线性系统的响应分析 3.1分析的目的 在已知外部输入 初始状态 系统状态响应 状态空 信号和系统初始 间模型 状态的情形下, 输入信号 根据状态空间模 线性系统 型来确定系统状 状态空 零输入响应 态的时间响应 初始状态 间模型 数学上可归结 系统状态响应 为求解系统的 状态空 输入信号 间模型 动态方程 零状态响应
第三章 线性系统的响应分析 3.1 分析的目的 在已知外部输入 信号和系统初始 状态的情形下, 根据状态空间模 型来确定系统状 态的时间响应 线性系统 数学上可归结 为求解系统的 动态方程

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 3.2零输入响应 零输入响应:输入信号0时系统由初始条件引起的响应 零输入响应可由齐次状态方程描述:(t)=Ax(t) 通常取初始时刻为,=0 方程的解具有以下形式:x(t)=e“x(O) 物理意义:将系统从初始时刻t的初始状态x(t)转移到t 时刻的状态x(t)。故Φ(t)=e"又称为状态转移矩阵 问题的关键:状态转移矩阵的计算
零输入响应: 输入信号u=0时系统由初始条件引起的响应 零输入响应可由齐次状态方程描述 : 3.2 零输入响应 x &(t) = Ax(t) x(t) e x(0) At = 物理意义: 将系统从初始时刻 的初始状态 转移到 时刻的状态 。故 又称为状态转移矩阵 0t t x(t) ( ) 0 x t 方程的解具有以下形式: 问题的关键: 状态转移矩阵的计算 通常取初始时刻为 t0 = 0 At Φ(t) = e

上誉文廷大¥ SHANGHAI JIAO TONG UNIVERSITY 拉氏变换法: 拉氏变换 (t)=Ax (t)sx(s)-x(0)=Ax(s) 整理 (sI-4)x(s)=x(O) 整理 拉氏逆变换 xs)=s-A)'xO)三>x)=L《s1-Ah0) *k9J2 x(t)-e4x(O)
拉氏变换法: sx(s)− x(0) = Ax(s) (sI − A)x(s) = x(0) ( )( ) (0) 1 x s sI A x − = − ( ) [( ) ] (0) 1 1 x t L sI A x − − = − [( ) ] −1 −1 e = L sI − A At x &(t ) = Ax (t ) 拉氏变换 拉氏逆变换 整理 整理 x(t) e x(0) At =

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 例3.2.1已知系统状态方程为 =2 初始条件为x0b 试求系统零输入响应 解: x(t)=er·x(0) 4[24
x x⎥⎦⎤ ⎢⎣⎡− − = 2 3 0 1 & ⎥⎦⎤ ⎢⎣⎡ = 01 x(0) 例3.2.1 已知系统状态方程为 初始条件为 试求系统零输入响应 解: ( ) = e ⋅ x(0) t t A x ⎥⎦⎤ ⎢⎣⎡ +− =⎥⎦⎤ ⎢⎣⎡− − −⎥⎦⎤ ⎢⎣⎡ − = 2 31 2 3 0 1 0 0 s s s s sI A

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 2 1 1 s+31 (SI-A)= 1 +1s+2 s+1S+2 (s+1)(s+2)-2 2 2 -1 2 S+1S+2 +1S+2 2e--e2 e-e21 0=e=Ls-0']=-2e+2e-e+ 则: mem-公2J川l e 2e--e-2 -2e+2e21
⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ + + + − + + + − + − + + − + =⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + + + − = − 2 2 1 1 2 2 1 2 2 1 1 1 2 1 1 2 2 3 1 ( 1)( 2 ) 1 ( ) 1 s s s s s s s s s s s s sI A 2 2 1 1 2 2 2e e e e ( ) e [( ) ] 2e 2e e 2e tt tt t t tt t Φ t Ls −− −− − − −− −− ⎡ − − ⎤ == − = ⎢ ⎥ ⎣− + −+ ⎦ A I A ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − + − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + − − = ⋅ = − − − − − − − − − − − − t t t t t t t t t t t t t t 2 2 2 2 2 2 2 e 2 e 2 e e 0 1 2 e 2 e e 2 e 2 e e e e x ( ) e x ( 0 ) A 则:

上誉文廷大¥ SHANGHAI JIAO TONG UNIVERSITY 3.3零状态响应 零状态响应:初始状态x(t,)=0时系统由输入信号引起 的响应 系统状态响应由非齐次状态方程描述:文=Ax+Bu x-Ax=Bu 移项 整理 e-4[x(t)-Ax(t)]=e-Bu(t) eBud)
零状态响应: 初始状态 时系统由输入信号引起 的响应 3.3 零状态响应 x& = Ax + Bu ( ) 0 x t 0 = x& − Ax = Bu 整理 系统状态响应由非齐次状态方程描述: 移项 e [ x ( t ) Ax ( t)] e Bu ( t ) − At − At & − = [e x( )t ] e Bu( )t dt d −At −At =

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 两边积分得 ex()=eBulry 系统零状态响应为 x(t)=[e-Bulr)dr 因此,线性系统的系统状态响应为零输入响应和零状态响 应的叠加 x()=eMx()+[e-Bu(r)dr
系统零状态响应为 () ( ) ( ) ( ) τ τ τ x t e x t e Bu d t At A t ∫ − = + 0 0 ( ) ( ) ( ) τ τ τ x t e Bu d t A t ∫ − = 0 因此,线性系统的系统状态响应为零输入响应和零状态响 应的叠加 两边积分得 () ( ) τ τ τ e x t e Bu d t At A ∫ − − = 0
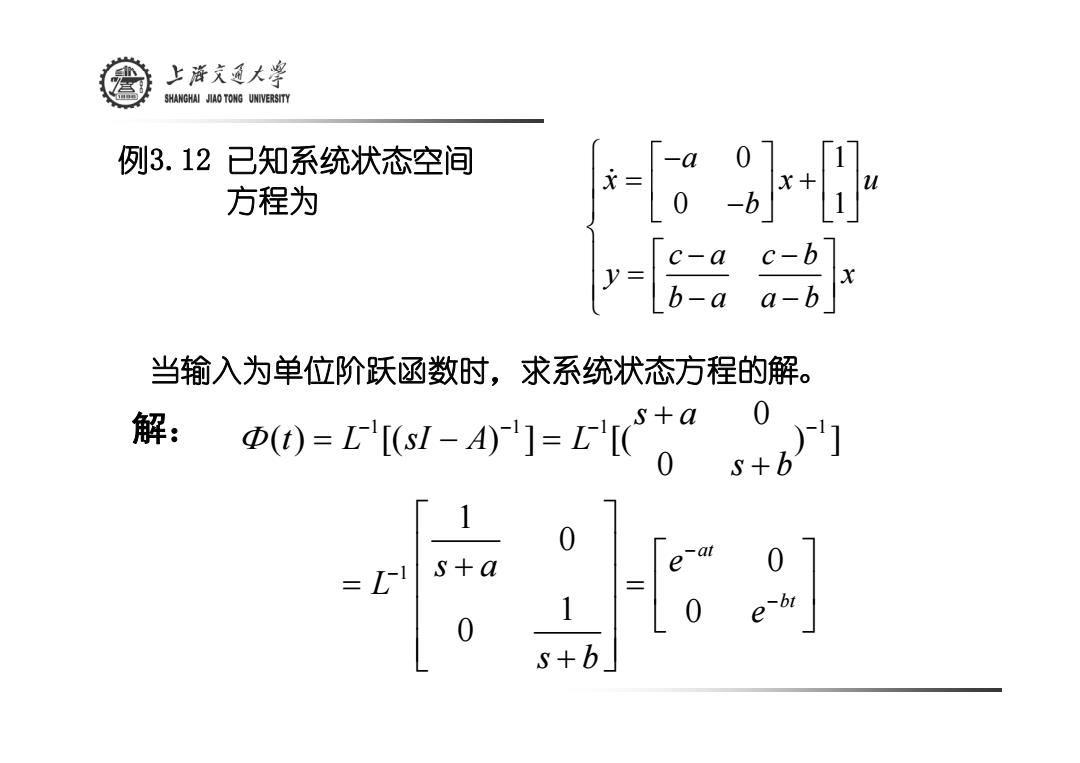
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 例3.12 已知系统状态空间 方程为 -b c-a y=b-a 当输入为单位阶跃函数时,求系统状态方程的解。 解: 0-a-I-Ers9g1 -at =L1 s+a 0 0
例3.12 已知系统状态空间 方程为 当输入为单位阶跃函数时,求系统状态方程的解。 0 1 0 1 a x xu b ca cb y x ba ab ⎧ −⎡ ⎤ ⎡⎤ ⎪ = + ⎢ ⎥ ⎢⎥ ⎪ ⎣ − ⎦ ⎣⎦ ⎨ ⎪ ⎡ ⎤ − − = ⎪ ⎢ ⎥ ⎩ ⎣ ⎦ − − & 解: 1 11 1 1 0 ( ) [( ) ] [( ) ] 0 1 0 0 1 0 0 at bt s a t L sI A L s b s a e L e s b Φ − −− − − − − + = − = + ⎡ ⎤ ⎢ ⎥ + ⎡ ⎤ = = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎢ ⎥ ⎣ ⎦ +

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY u(t)=1() .x()=()x(0)+(t-)Bu()dt 8mgl 0小 1-e)+ex(0) a
0 ( ) 1 ( ) 0 2 ( ) 1 1 ( ) 0 2 2 ( ) ( ) (0) ( ) ( ) 0 0 (0) 1 0 0 (0) 1 1 (1 ) (0) (0) (0) 1 (1 ) (0) t at a t t bt b t at at at a t t bt b t bt bt x t t x t Bu d e e x d e e x e ex e x e a d e x e e ex b τ τ τ τ Φ Φ τ ττ τ τ − −− − −− − − − − − − − − − − ∴= + − ⎡⎤ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ = + ⎢⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎡ − + ⎡ ⎤ ⎢ ⎡ ⎤ =+ = ⎢ ⎥ ⎢ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ − + ⎣ ∫ ∫ ∫ ⎤ ⎥ ⎥ ⎢ ⎥ ⎢ ⎥⎦ u(t)=1( t)

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 32 作业2如图的RLC电路, 0.5F 选X1=i,X2=uc,y=ue, 状态空间描述为 母 少设4,=0,七周,计算系统的零箱入响应 2)设u(t)=l(t),计算系统的零状态响应
作业2 如图的RLC电路, 选 , 状态空间描述为 ~ u 3Ω y 1H 0.5F + − + − c c x = i, x = u , y = u 1 2 [ ] ⎥⎦⎤ ⎢⎣⎡ = ⎥⎦⎤ ⎢⎣⎡ ⎥ +⎦⎤ ⎢⎣⎡⎥⎦⎤ ⎢⎣⎡− − ⎥ =⎦⎤ ⎢⎣⎡ 2 1 2 1 2 1 0 1 0 1 2 0 3 1 x x y u x x x x & & 2)设 ,计算系统的零状态响应 u(t) =1(t) 1) 设 , ,计算系统的零输入响应 t 0 = 0 ⎥⎦⎤ ⎢⎣⎡ = 01 x0