
第五章 最小实现
第五章 最小实现

5.1引言 建立系统的状态空间描述的方法: 机理建模:系统的物理机理、结构和参数→系统的状 态空间描述 模型转换:系统的传递函数阵→系统的状态空间描述 根据系统的传递函数阵求取系统的状态空间描述的问题 称为实现(realization)问题。求得的状态空间描述是该传 递函数阵的一个实现。 现实系统分为两大类:正常系统(式(5一1)所示)和奇 异系统或广义系统(式(5-9)所示) 本章只讨论正常系统的实现问题
5.1 引 言 建立系统的状态空间描述的方法: 机理建模:系统的物理机理、结构和参数 系统的状 态空间描述 ⇒ 模型转换:系统的传递函数阵 系统的状态空间描述 ⇒ 根据系统的传递函数阵求取系统的状态空间描述的问题 称为实现( )问题。求得的状态空间描述是该传 递函数阵的一个实现。 realization 现实系统分为两大类:正常系统(式(5-1)所示)和奇 异系统或广义系统(式(5-9)所示)。 本章只讨论正常系统的实现问题

·正常系统的实现问题: 已知传递函数阵G),如果存在一个有限维的状态空间描述 (t)=Ax(t)+Bu(t) (5-1) y(t)=Cx(t)+Du(t) 式(5一1)的模型可简单表示为(4,B,C,D),满足 G(s)=C(sI-A)B+D 则称A,B,C,D)是G(s)的一个实现。 ●实现研究的问题 (1)G(s)可实现为(4,B,C,D)的条件问题 (2)G(s)实现的方法
正常系统的实现问题: 已知传递函数阵 ,如果存在一个有限维的状态空间描述 G(s) x( ) Ax( ) Bu( ) y( ) Cx( ) Du( ) & t tt ttt = + = + (5-1) 式(5—1)的模型可简单表示为 ,满足 (A,B,C, D) 1 G( ) C( I A) B D s s − =− + 则称 是 的一个 (A,B,C, D) G(s) 实现。 • • 实现研究的问题 ⑴ 可实现为 的条件问题 G(s) ⑵ G(s) 实现的方法 (A,B,C, D)

·最小实现 如果(A,B,C,D)是G(s)的一个实现,则其所有等价系统也都是其 实现。 G(s)可有不同维数的实现,其中维数最小的实现称为最小实 现。它描述了系统的既能控又能观的部分。通常要求的实现 为最小实现。 ●本章内容: G(s)可实现的条件。 最小实现的方法:单变量系统的最小实现。 多变量系统的最小实现
本章内容: 可实现的条件。 最小实现的方法:单变量系统的最小实现。 多变量系统的最小实现。 •最小实现 如果 是 的一个实现,则其所有等价系统也都是其 实现 。 (A,B,C, D) G(s) G(s) • 可有不同维数的实现,其中维数最小的实现称为最小实 现。它描述了系统的既能控又能观的部分。通常要求的实现 为最小实现。 G(s)

5.2实现和最小实现 5.2.1Gs)可实现为正常系统的条件 (1)传递函数(阵)的正则性 有理函数8)= d(s), 分子与分母多项式ns和s的次数 分别记为6n(s)和6d(s)。 定义有理函数gs)当s一∞时, 若g(oo)=常数(6n(s)=6ds),g就称为正则有理函数。 若g(o)=0(6n(s)()),gs)就是非正则有理函数
5.2 实现和最小实现 5.2.1 可实现为正常系统的条件 G(s) ⑴ 传递函数(阵)的正则性 有理函数 ,分子与分母多项式 和 的次数 分别记为 和 。 ( ) ( ) ( ) n s g s d s = n (s) d(s) δ ( ) n s δ d (s) ① 定义 有理函数 当 时, 若 常数( ), 就称为正则有理函数 。 若 ( ), 就是严格正则有理函数 。 若 ( ), 就是 非正则有理函数 。 g(s) s → ∞ g( ) ∞ = δ δ n s ds () () = g(s) g() 0 ∞ = δ δ n s ds () () δd(s)

有理函数阵G(s) 若G(o=0, 则G()是严格正则有理函数阵(其每个元均为 6n(s)s))。 正则也称真,严格正则也称严格真,非正则也称非真。 传递函数阵 G(s)=C(sI-A)B+D 其正则性由下式判定 0 严格正则 lim G(s)= D 正则 (5-2) 、0 非正则
有理函数阵 若 ,则 是严格正则有理函数阵(其每个元均为 )。 若 , 是常数阵, 是正则有理函数阵(其每个元 均为 ,且至少一个元 )。 若 (至少一个元为 ),则 是非正则有理函数 阵(至少一个元 )。 G(s) G(∞) = 0 G(∞) = D G(s) G(s) δ n (s) δd(s) δ n (s) = δd(s) ∞ G(s) 正则也称真,严格正则也称严格真,非正则也称非真。 传递函数阵 G = C I − A B + D −1 (s) (s ) 其正则性由下式判定 ⎪⎩ ⎪⎨⎧ ∞ = →∞ D 0 lim G(s) s 严格正则 正则 非正则 (5-2)

2 不可简约传递函数s)阶次 正则有理函数(s)的阶次 正则有理函数gs)是一个有理分式(多项式分式) 8(s)= n(s) d(s) (5-3) 一般可写成 g(s)= n(s)r(s) d(s)r(s) (5-4) 式中,()为任意多项式,表示分子、分母的公因子。 传递函数是系统的输入输出描述,描述的是系统既能控又能 观部分,它总是互质的。如果没有说明,传递函数定义为不 可简约的,即s)和d(s)是互质的或没有公因子,并且总是把ds) 化为首一多项式。 称ds)为)的特征多项式,并将传递函数s)的阶次定义为 特征多项式d(s)的阶次,记为degg(s)
② 不可简约传递函数 阶次 正则有理函数 的阶次 g(s) 正则有理函数 是一个有理分式 g(s) (多项式分式 ) ( ) ( ) ( ) d s n s g s = g(s) (5-3) 一般可写成 ( ) ( ) ( ) ( ) ( ) d s r s n s r s g s = (5-4) 式中, 为任意多项式,表示分子、分母的公因子。 r(s) 传递函数是系统的输入输出描述,描述的是系统既能控又能 观部分,它总是互质的。如果没有说明,传递函数定义为不 可简约的,即 和 是互质的或没有公因子,并且总是把 化为首一多项式。 n(s) d(s) d(s) 称 为 的特征多项式,并将传递函数 的阶次定义为 特征多项式 的阶次,记为 。 d(s) g(s) g(s) d(s) deg g(s)

例5-1 8(s)= (s-1)2 3(s3-1) s-1是分子、分母的公因子,所以g)的互质分式为 s+1 3s2+s+1)) 特征多项式为(s2+s+1),degg(s)=2。 ③不可简约传递函数阵G(s)的特征多项式是:G(s)的所有子 式的首一最小公倍分母(简称最小公分母)。 G(s)的特征多项式的阶次定义为Gs)的阶次,记为dgGs)。 在计算Gs)的特征多项式时,所有子式都必须是不可简约的 或互质的
例5-1 3( 1) ( 1) ( ) 3 2 − − = s s g s 是分子、分母的公因子,所以 的互质分式为 , 特征多项式为 , 。 s −1 g(s) 3( 1) 1 2 + + + s s s ( 1) 2 s + s + deg g(s) = 2 ③ 不可简约传递函数阵 的特征多项式是: 的所有子 式的首一最小公倍分母(简称最小公分母)。 G(s)的特征多项式的阶次定义为 的阶次,记为 。 G(s) G(s) G(s) degG(s) 在计算 的特征多项式时,所有子式都必须是不可简约的 或互质的。 G(s)

例5-2 1 G(s)= S+1 S+1 1 1 3(s+1) 3(s+1) 111 一次子式:一次子式是G(s)的所有诸元,即+1,s+1,3s+D 1 3(s+1) 二次子式:二次子式是G(s)的所有2×2的二次行列式,本例 中只有 1111 0 3s+)s+13s+Ds+1 G(s)的特征多项式(所有子式的首一最小公分母)是s+1,dgGs)=1。 即该传递函数阵是1阶的
例5-2 ⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡ + + + + = 3( 1) 1 3( 1) 1 1 1 1 1 ( ) s s s s G s 一次子式:一次子式是 的所有 诸元,即 , , , ; 3( 1) 1 s + , 1 1 s + , 1 1 s + , 3( 1) 1 s + ; 二次子式:二次子式是 的所有 的二次行列式,本例 中只有 0 1 1 3( 1) 1 1 1 3( 1) 1 = + × + − + × s + s s s 的特征多项式(所有子式的首一最小公分母)是, 。 即该传递函数阵是1阶的。 G(s) s +1 degG(s) =1 G(s) G(s) 2× 2
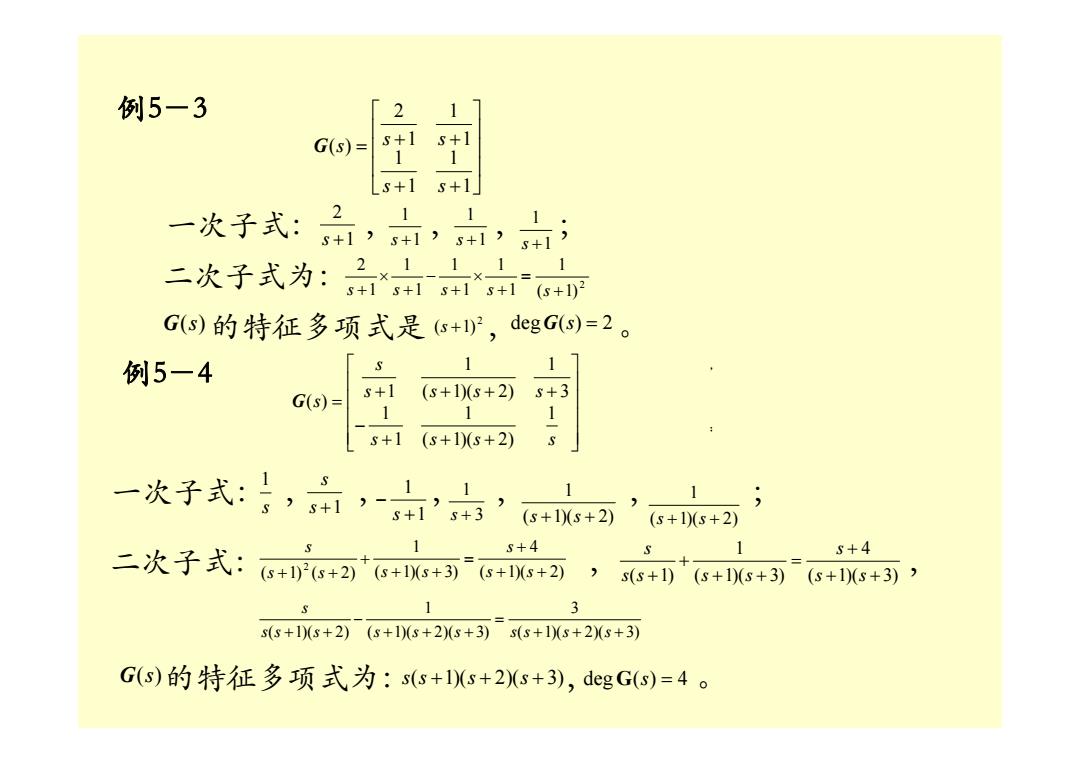
例5-3 2 1 G(s)= S+1 s+1 1 1 Ls+1 s+1 一次子式: 11 1 S+1)s+12s+1’ 5+1) 二次子式为:2×11x1 、1 s+1s+1s+1s+1(s+1)2 G(s)的特征多项式是s+12,degG(s)=2。 例5-4 1 1 G(s)= S+1 (s+1)(s+2) +3 1 1 1 s+1 (s+1)(s+2) 一次子式: 1 1 S+1s+3 (s+1)(s+2) (s+1)(s+2) 二次子式: S 1 S+4 S 1 S+4 (s+1)2(s+2)(s+1(s+3)(s+10(s+2)) s(s+1)(s+1)(s+3)(s+1)(s+3)’ 1 3 s(s+1)(s+2)(s+1)(s+2)(s+3)s(s+1)(s+2)(s+3) G(s)的特征多项式为:s(s+1)s+2s+3),dgG(s)=4
例5-3 ⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡ + + + + = 1 1 1 1 1 1 1 2 ( ) s s s s G s 一次子式: 1 ,,,; 2s + 1 1 1 s + 1 1 s + 1s + 二次子式为: 2 ( 1) 1 1 1 1 1 1 1 1 2 + = + × + − + × s + s s s s G(s)的特征多项式是 , 。 2 (s +1) degG(s) = 2 例5-4 ⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡ + + + − + + + + = s s s s s s s s s s 1 ( 1)( 2) 1 1 1 3 1 ( 1)( 2) 1 1 G( ) 一次子式: , , , , , ; 二次子式: , , s 1 s +1 s 1 1 + − s 3 1 s + ( 1)( 2) 1 s + s + , ( 1)( 2) 1 s + s + ; ( 1)( 2) 4 ( 1)( 3) 1 ( 1) ( 2) 2 + + + = + + + + + s s s s s s s s ( 1)( 3) 4 ( 1)( 3) 1 ( 1) + + + = + + + + s s s s s s s s ( 1)( 2)( 3) 3 ( 1)( 2)( 3) 1 ( 1)( 2) + + + = + + + − s s + s + s s s s s s s s G(s)的特征多项式为: , 。 s(s +1)(s + 2)(s + 3) degG(s) = 4