
上誉文通大¥ SHANGHAI JIAO TONG UNIVERSITY 第四章能控性和能观性 4.1问题的提出 ®状态方程一反映控制输入对状态的影响 (t)=Ax+Bu ®输出方程一反映系统输出对控制输入和状态的依赖 y=Cx+Du ©响应分析一反映初始状态和输入对系统运行状况的影响 x(to),u(t)→x(t)
状态方程-反映控制输入对状态的影响 输出方程-反映系统输出对控制输入和状态的依赖 响应分析-反映初始状态和输入对系统运行状况的影响 第四章 能控性和能观性 4.1 问题的提出 ( ), ( ) ( ) 0 x t u t → x t x&( t ) = Ax + Bu y = Cx + Du

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 两个基本问题: 1)在有限时间内,控制作用能否使系统从初始状态转移 到要求的状态? 指控制作用对状态变量的影响或控制能力,称之为状 态能控性问题一决定能否实现最优控制 2)在有限时间内,能否通过对系统输出的测定来估计系 统的各个状态? 指系统的输出量对系统状态的识别能力,称之为状态 能观性问题一决定能否实现状态反馈控制
1)在有限时间内,控制作用能否使系统从初始状态转移 到要求的状态? 指控制作用对状态变量的影响或控制能力,称之为状 态能控性问题-决定能否实现最优控制 两个基本问题: 2)在有限时间内,能否通过对系统输出的测定来估计系 统的各个状态? 指系统的输出量对系统状态的识别能力,称之为状态 能观性问题-决定能否实现状态反馈控制

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 例4.1.1分析以下系统的能控性和能观性: X2 L] y=[0-6]x 展开得 =4x+ux2=-5x2+2u y=-6x2 结论:状态变量X1、x2都可通过选择输入而控制 输出y只能反映状态变量x2,所以x1不能观测
结论:状态变量 、 都可通过选择输入 u而控制 输出 y只能反映状态变量 ,所以 不能观测 例4.1.1 分析以下系统的能控性和能观性: y [ ] x u x x x x 0 6 2 1 0 5 4 0 2 1 2 . 1 . = − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ 2 1 1 2 2 6 4 5 2 y x x x u x x u = − & = + & = − + 1 x 2 x 展开得 2 x 1 x

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 例4.1.2老虑以下的 RLC网终 R R 选择电感中的电流以及 u(t) 电容上的电压作为状态 变量,电容上的电压为 R 输出变量,即 =il,x2=uc,y=uc 当R1R4≠R2R3,即电桥不平衡时,输入能控制x1和x2,系 统是能控的
例4.1.2 考虑以下的 RLC网络 选择电感中的电流以及 电容上的电压作为状态 变量,电容上的电压为 输出变量,即 当R1R4≠R2R3,即电桥不平衡时,输入u能控制x1和x2,系 统是能控的 L c c x = i , x = u , y = u 1 2 & & u(t) + − R1 R2 R4 Li uc R3

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 例4.1.3老虑以下的 RLC网络 R u(t) R 同样取 x=il,x2=uc,y=ue 当R1R4=R2R3,即电桥平衡时,电感中的电流作为电路的一 个状态是不能由输出变量来确定的,该系统是不能观测的
例4.1.3 考虑以下的 RLC网络 同样取 当R1R4=R2R3,即电桥平衡时,电感中的电流作为电路的一 个状态是不能由输出变量来确定的,该系统是不能观测的 L c uc x & 1 = i , x&2 = u , y = u(t) + − R1 R2 R4 Li R3 c u

上誉文通大¥ SHANGHAI JIAO TONG UNIVERSITY 4.2能控性的定义 状态方程 (t)=Ax+Bu 能控性: u(t)→x(t) 定义: 如果存在一个分段连续的输入能在有限时间间隔内,使 得系统从任意一个初始状态转移到任意的终止状态,则 称此系统是状态完全能控的,简称系统是能控的
4.2 能控性的定义 x &(t) = Ax + Bu 状态方程 能控性: 定义: 如果存在一个分段连续的输入能在有限时间间隔内,使 得系统从任意一个初始状态转移到任意的终止状态,则 称此系统是状态完全能控的,简称系统是能控的 u(t) → x(t)
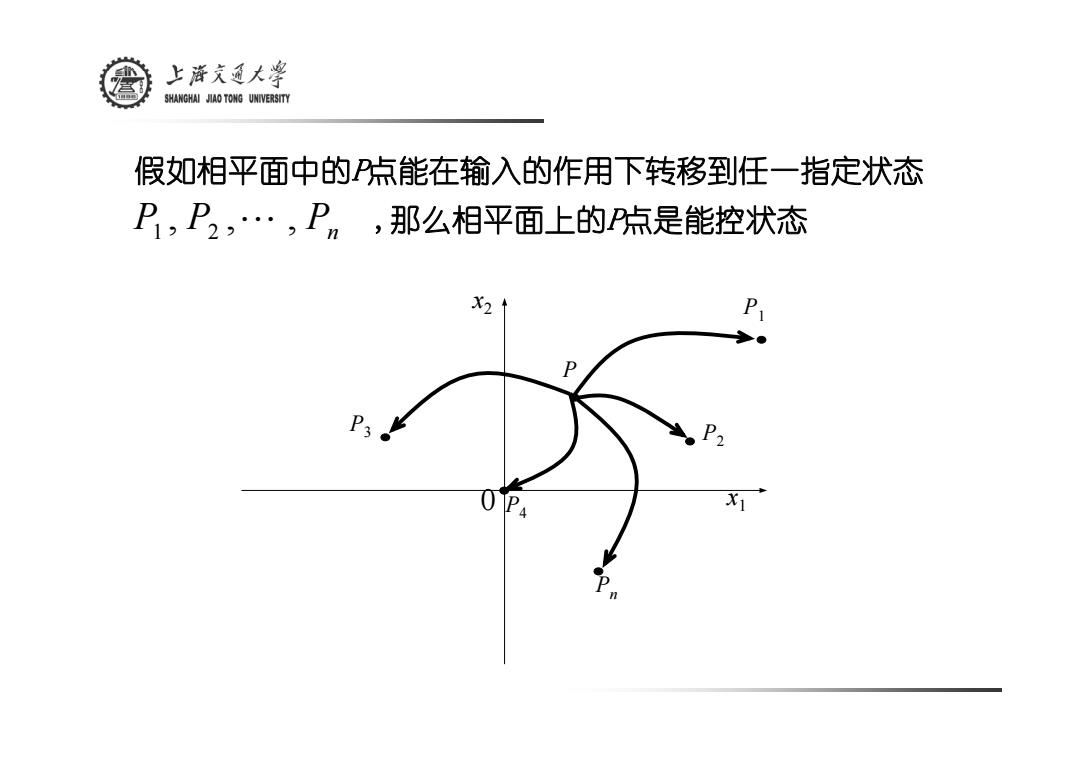
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 假如相平面中的点能在输入的作用下转移到任一指定状态 P,P2,…,P,,那么相平面上的P点是能控状态 P ● P D
假如相平面中的P点能在输入的作用下转移到任一指定状态 P1 2 ,,, P P L n ,那么相平面上的P点是能控状态 P P3 P1 P2 Pn P4 0 x1 x2
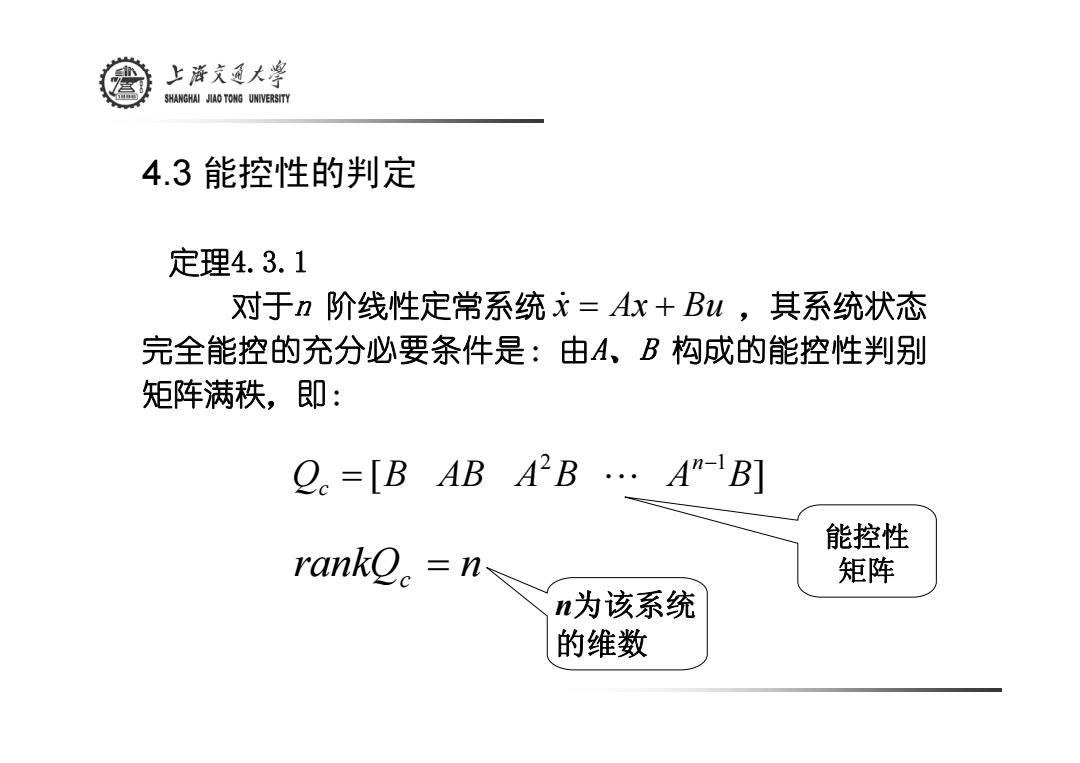
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 4.3能控性的判定 定理4.3.1 对于n阶线性定常系统x=Ax+Bu,其系统状态 完全能控的充分必要条件是:由A、B构成的能控性判别 矩阵满秩,即: Q。=[B AB A2B·A-B] 能控性 rankO。=n 矩阵 n为该系统 的维数
定理4.3.1 对于n 阶线性定常系统 ,其系统状态 完全能控的充分必要条件是:由A、B 构成的能控性判别 矩阵满秩,即: x & = Ax + Bu [ ] 2 1 Q B AB A B A B n c − = L rankQc = n n为该系统 的维数 能控性 矩阵 4.3 能控性的判定

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 例4.3.1判别下列状态方程的能控性。 (1) 小* 解:(1)n=2 Q.=B AB A'B…A-B -a8侧-0 rankO。=1<n .系统状态不完全能控
x x u⎥⎦⎤ ⎢⎣⎡ + ⎥⎦⎤ ⎢⎣⎡ − − = 01 0 1 2 1 & 例4.3.1 判别下列状态方程的能控性。 Q [B AB A B A B] n c 2 −1 = L rankQ n c = 1 < ∴ 系统状态不完全能控。 解:(1) n = 2 ⎥⎦⎤ ⎢⎣⎡ − = = 0 0 1 2 [B AB] (1)
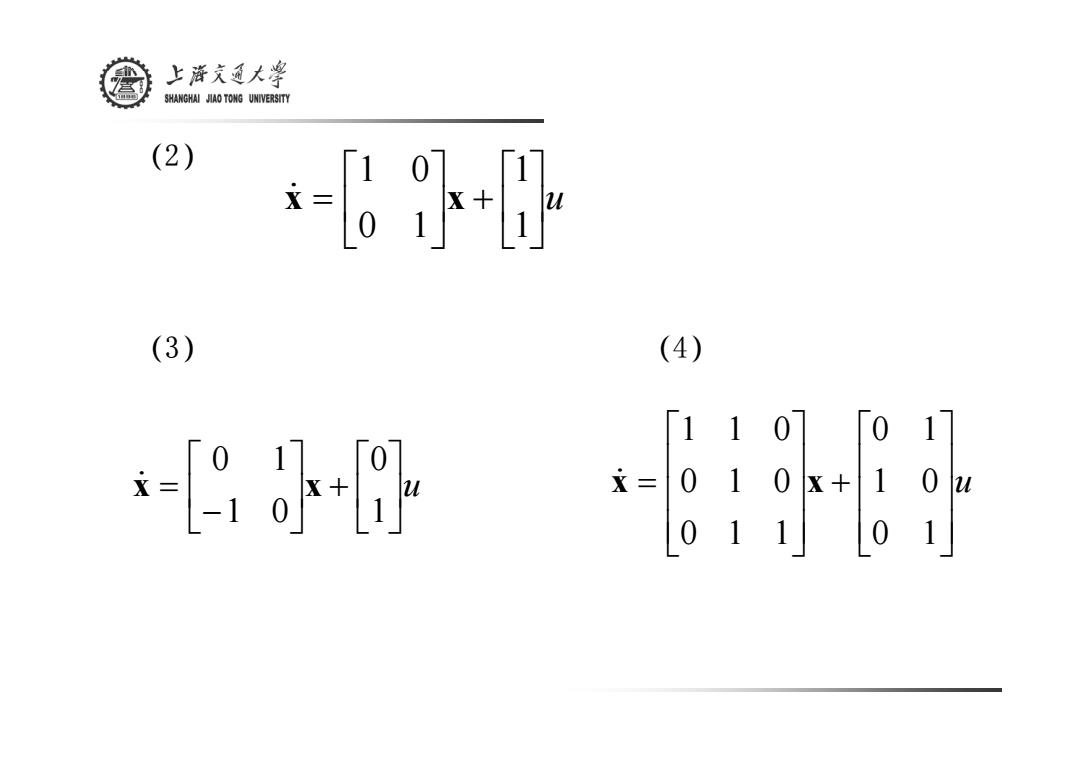
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY (2) 6出 (3) (4) s9小 110 [0 1583
(2) (3) (4) u⎥⎦⎤ ⎢⎣⎡ + ⎥⎦⎤ ⎢⎣⎡ = 11 0 1 1 0 x& x u⎥⎦⎤ ⎢⎣⎡ ⎥ + ⎦⎤ ⎢⎣⎡− = 10 1 0 0 1 x& x u⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡ + ⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡ = 0 1 1 0 0 1 0 1 1 0 1 0 1 1 0 x& x