
第四章 自适应线性神经元 辈自适应线性神经元模型 单个自适应线性神经元的学习方法 辈单层自适应线性神经元的学习方法 奉MATLAB程序仿真 集关于自适应线性神经元的几点说明 2006-11-28 北京科技大学付冬梅
2006-11-28 北京科技大学 付冬梅 2 第四章 自适应线性神经元 自适应线性神经元模型 单个自适应线性神经元的学习方法 单层自适应线性神经元的学习方法 MATLAB程序仿真 关于自适应线性神经元的几点说明

4.1自适应线性神经元模型 线性神经元模型如图所示: I/O关系 a=purelin(W*P+b) 输入 具有向量输入的线性神经元 此处 R=输入神经元 的个数 a purelin(Wp+b) 2006-11-28 北京科技大学付冬梅 3
2006-11-28 北京科技大学 付冬梅 3 4.1自适应线性神经元模型 线性神经元模型如图所示: I/O关系 a=purelin(W*P+b)
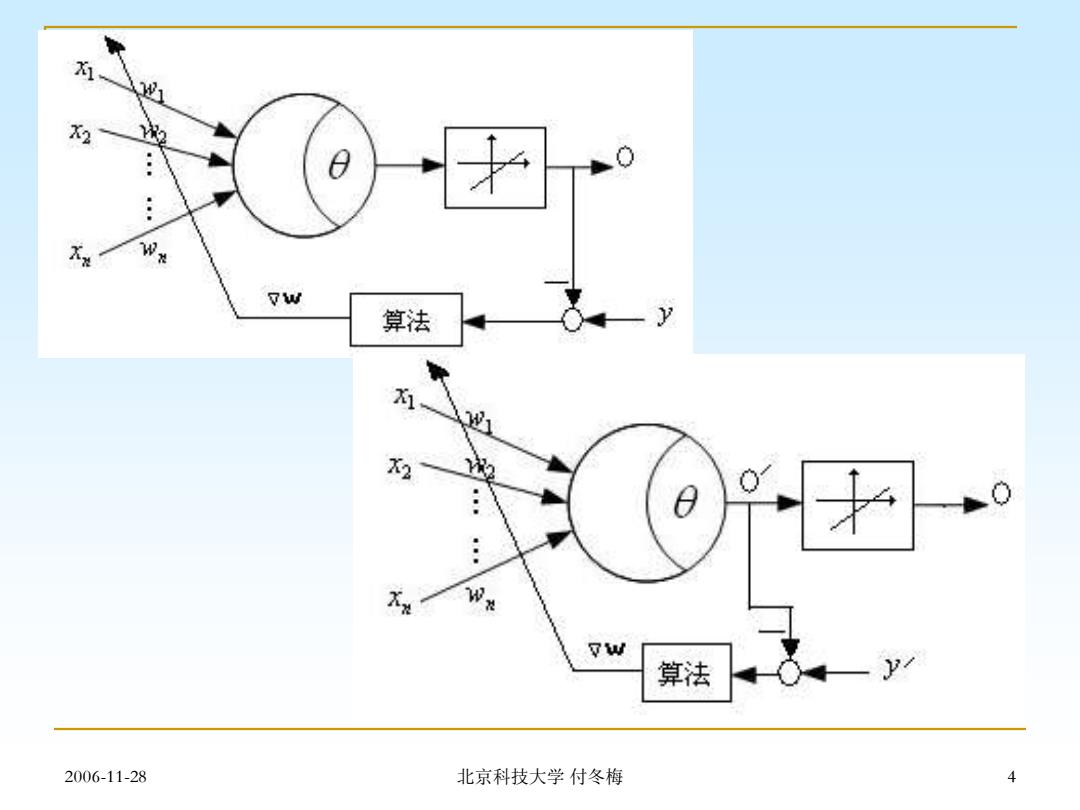
X2 : : w 算法 X2 4 w 算法 2006-11-28 北京科技大学付冬梅 4
2006-11-28 北京科技大学 付冬梅 4
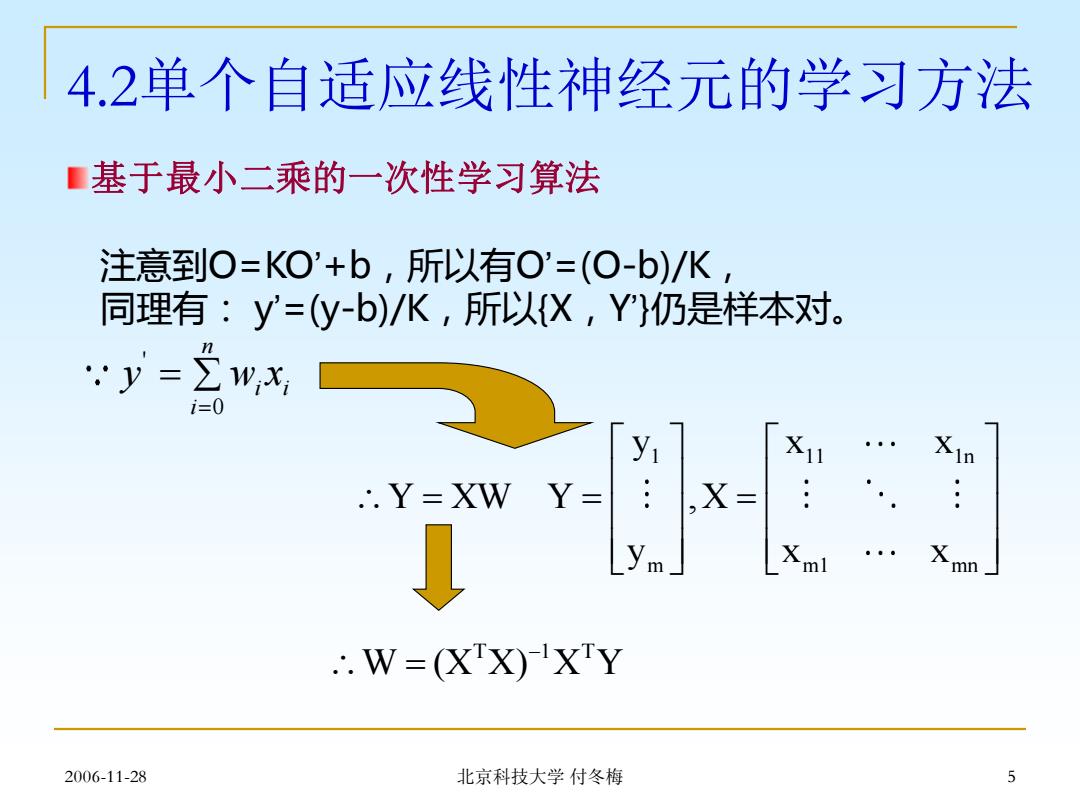
4.2单个自适应线性神经元的学习方法 ■基于最小二乘的一次性学习算法 注意到O=KO'+b,所以有O'=(O-b)/K 同理有:y=y-b)/K,所以X,Y仍是样本对。 y=∑w,x i=0 y X 10 ..Y=XW Y= X ym ∴.W=XX)XY 2006-11-28 北京科技大学付冬梅 5
2006-11-28 北京科技大学 付冬梅 5 基于最小二乘的一次性学习算法 4.2单个自适应线性神经元的学习方法 注意到O=KO’+b,所以有O’=(O-b)/K, 同理有: y’=(y-b)/K,所以{X,Y’}仍是样本对。 ' 0 n i i i y w x = = 1 11 1n m m1 mn y x x Y XW Y ,X y x x = = = W (X X) X Y T 1 T − =

4.2单个自适应线性神经元的学习方法 基于梯度的学习算法(内部反馈) 设经过no次学习以后(即得到第n0个W1w2·wn 后,或者没有初始权值w°w…w后),对于输入x, 感知机的输出为: y(n)=∑w,(n)x=WIX 其中 1Wn+1=-8 Xn+1三1 又设在同样输入X作用下,样本输出y则感知机的输出误差为 e(no)=y-y(no)e2(no)=[y-y(no)] 2006-11-28 北京科技大学付冬梅 6
2006-11-28 北京科技大学 付冬梅 6 基于梯度的学习算法(内部反馈) 后),对于输入 , n0 次学习以后(即得到第 n0 个 w w w 1 2 n j x T j n i j y n wi n xi W X + = = = 1 1 0 0 ( ) ( ) wn+1 = − xn+1 1 ( ) ( ) 0 n0 e n y y j = − 2 0 0 2 e (n ) [ y y(n )] j = − 设经过 后,或者没有初始权值 感知机的输出为: 其中 则感知机的输出误差为: j x j 又设在同样输入 作用下,样本输出 y 1 2 0 0 0 w w wn 4.2单个自适应线性神经元的学习方法

4.2单个自适应线性神经元的学习方法 根据建立在梯度法基础上的最小均方差(LMS)算法得知, 被调整的参数(这里是W「)的修改应该向着梯度的反方向进行, 即:W(no+l)=W(no)-n7(no) 此处梯度为:(no)= de2(no)d(y-W'(no)X) =-2e(n) ow(no) aw(no) 因此我们有:W(n。+1)=W(no)+27e(no)XJ 根据上面的推导,我们可以给出感知器(单个且()=少 权值调整的具体学习步豫: (1)随机初始化权值和阈值: w,(0)=a.random()a≠0,i=1,2,…,n+1 2006-11-28 北京科技大学付冬梅
2006-11-28 北京科技大学 付冬梅 7 根据上面的推导,我们可以给出感知器(单个且 ) 根据建立在梯度法基础上的最小均方差(LMS)算法得知, 被调整的参数(这里是 T W ( 1) ( ) ( ) W n0 + = W n0 − n0 j j T j e n X W n y W n X W n e n n 2 ( ) ( ) ( ( ) ) ( ) ( ) ( ) 0 0 2 0 0 0 2 0 = − − = = j W (n0 +1) =W (n0 ) + 2e(n0 )X f (u) = u )的修改应该向着梯度的反方向进行, 此处梯度为: 因此我们有: 权值调整的具体学习步骤: 即: (1)随机初始化权值和阈值: (0) random( ) 0, 1,2, , 1 w a a i n i = = + 4.2单个自适应线性神经元的学习方法

4.2单个自适应线性神经元的学习方法 (2)在A样本集合{A,B}中,任选一个x或xB作为输入向量, 比如选中xA中的x作为本次的训练,并以此为输入计算 感知机的输出:y=f(WrX) (3)若y=1,则表明分类正确,而不需要调整权值和阈值,如此 可回到(2)步,并重新选一个新的训练样本。如果y=-1 ,表明将X错分到X°类中了,需按下面步骤调整权值。 (4)设no为送代次数,按: w,(n+1)=w,(n)+27y-y'(n)x(n,) 其中:t,4是理想输出,即样本输出)调整权值,此处门 为学习率。y=1为期望输出,直到计算y=】为止。 2006-11-28 北京科技大学付冬梅 8
2006-11-28 北京科技大学 付冬梅 8 为迭代次数,按: 作为输入向量, ,则表明分类正确,而不需要调整权值和阈值,如此 错分到 类中了,需按下面步骤调整权值。 中的 作为本次的训练,并以此为输入计算 A B x 或x A x x ( ) l T l y = f W X 比如选中 (2)在A样本集合{A,B}中,任选一个 感知机的输出: =1 l y = −1 l y l x B ,表明将 x (3)若 可回到(2)步,并重新选一个新的训练样本。如果 0 n 0 0 0 0 ( 1) ( ) 2 (y ( )) ( ) l l w n w n y n x n i i i + = + − qA t y 1 = y = 1 其中: 是理想输出,即样本输出)调整权值,此处 为学习率。 为期望输出,直到计算 为止。 (4)设 4.2单个自适应线性神经元的学习方法

4.2单个自适应线性神经元的学习方法 (5)重新在A,B样本集中选择另一个样本进行学习,即 重复(2)~(5),直到 w,(no+1)=w,(no) 对所有i=1,2,…,n+1均成立,对所有样本均正确 分类,则学习结束。 说明:①上面的算法适合f(u)=ku+b这样连续激动函数,但是 此时不能用y(n)=1或-1来作为迭代的标准,往往以误差 大小作为限制,即在算法的第(3)步中,|y-yKe 则不要调整权值,否则进行(4)步。 ②理想输出不一定非得是+1或-1,可以使其他的实数。 2006-11-28 北京科技大学付冬梅 9
2006-11-28 北京科技大学 付冬梅 9 ( 1) ( ) 0 0 w n w n i + = i i =1,2, , n +1 (5)重新在A,B样本集中选择另一个样本进行学习,即 重复(2)~(5),直到 对所有 均成立,对所有样本均正确 分类,则学习结束 。 f u ku b ( ) = + y (n0 ) =1或 −1 l | y | l y e − ①上面的算法适合 这样连续激励函数,但是 来作为迭代的标准,往往以误差 ,则不要调整权值,否则进行(4)步。 说明: 此时不能用 大小作为限制,即在算法的第(3)步中, ②理想输出不一定非得是+1或-1,可以使其他的实数。 4.2单个自适应线性神经元的学习方法

4.2单个自适应线性神经元的学习方法 基于梯度的学习算法(外部反馈) 设经过no次学习以后(即得到第n0个W1w2·wn 后,或者没有初始权值w°w…w后),对于输入x 感知机的输出为: n+ y(no)=k w;(no)x+b=kw'Xi+b i- 其中 Wn+l =-0 Xn+1三1 又设在同样输入X作用下,样本输出y则感知机的输出误差为 e(no)=y-y(no)e2(no)=[y-y(no)] 2006-11-28 北京科技大学付冬梅 10
2006-11-28 北京科技大学 付冬梅 10 基于梯度的学习算法(外部反馈) 后),对于输入 , n0 次学习以后(即得到第 n0 个 w w w 1 2 n j x 1 0 0 1 ( ) ( ) n j T j i i i y n k w n x b kW X b + = = + = + wn+1 = − xn+1 1 ( ) ( ) 0 n0 e n y y j = − 2 0 0 2 e (n ) [ y y(n )] j = − 设经过 后,或者没有初始权值 感知机的输出为: 其中 则感知机的输出误差为: j x j 又设在同样输入 作用下,样本输出 y 1 2 0 0 0 w w wn 4.2单个自适应线性神经元的学习方法

4.2单个自适应线性神经元的学习方法 基于梯度的学习算法(外部反馈) 根据建立在梯度法基础上的最小均方差(LMS)算法得知, 被调整的参数(这里是W)的修改应该向着梯度的反方向进行, 即:W(n+1)=W(no)-n(n) 此处梯度为: (n)= de2(n) dy-kW"(n )X-b)=-2ke(n) w(n) ow(n) 因此我们有: W(no+1)=W(no)+2nke(no)X 2006-11-28 北京科技大学付冬梅
2006-11-28 北京科技大学 付冬梅 11 根据建立在梯度法基础上的最小均方差(LMS)算法得知, 被调整的参数(这里是 T W ( 1) ( ) ( ) W n0 + = W n0 − n0 2 2 0 0 0 0 0 0 ( ) ( ( ) ) ( ) 2 ( ) ( ) ( ) j T j e n y kW n X b j n ke n X W n W n − − = = = − 0 0 0 ( 1) ( ) 2 ( ) j W n W n ke n X + = + )的修改应该向着梯度的反方向进行, 此处梯度为: 因此我们有: 即: 4.2单个自适应线性神经元的学习方法 基于梯度的学习算法(外部反馈)