
研究实验9报告示范一模糊神经网络与模糊控制的算 法研究 一.研究问题描述: 用模糊控制的方法对含有噪声的不稳定二阶系统进行控制,并与PD方法 的控制结果进行比较。系统离散化方程为: y(k)=0.36y(k-1)-0.132(k-2)+0.117(k-1)+0.076u(k-2)+v(k) 二、要求 1、模糊神经网络结构的选择、实现及其影响的仿真与分析: 2、所用算法的理论描述和程序流图: 3、算法中参数选择的影响分析与仿真; 4、仿真结果的分析与说明。 三.网络结构: 采用二维模糊控制器,模糊控制器的输入系统误差和误差的变化量e和△e分 别划分为7段,均取三角形隶属函数,可产生49条模糊控制规则,经过优化得 到21条规则。如图1所示,系统由四层神经网络构成,功能上分为输入层、模 糊化层、模糊规划层和去模糊化层。输入层为网络输入变量误差x=,,误差变 化x,=△。模糊化层节点的激活函数代表模糊变量的隶属函数,该层的权值o.表 示隶属函数的形状,0。=c表示隶属函数的位置,该层的输出代表模糊化的结果, 即把确定量转化成了隶属度。模糊规则层将上一层模糊化得到的结果两两相乘, 代表模糊规则的规则强度。将模糊规则层的结果传递给去模糊化层。去模糊化层 的各个权值⊙代表模糊规则,根据重心法的去模糊化公式,把规则强度加权求和, 输出即为模糊控制器的输出量
研究实验 9 报告示范——模糊神经网络与模糊控制的算 法研究 一.研究问题描述: 用模糊控制的方法对含有噪声的不稳定二阶系统进行控制,并与 PID 方法 的控制结果进行比较。系统离散化方程为: y k y k k u k u k v k ( ) 0.36 ( 1) 0.132( 2) 0.117 ( 1) 0.076 ( 2) ( ) = − − − + − + − + 二、要求 1、模糊神经网络结构的选择、实现及其影响的仿真与分析; 2、所用算法的理论描述和程序流图; 3、算法中参数选择的影响分析与仿真; 4、仿真结果的分析与说明。 三.网络结构: 采用二维模糊控制器,模糊控制器的输入系统误差和误差的变化量 e 和 e 分 别划分为 7 段,均取三角形隶属函数,可产生 49 条模糊控制规则,经过优化得 到 21 条规则。如图 1 所示,系统由四层神经网络构成,功能上分为输入层、模 糊化层、模糊规划层和去模糊化层。输入层为网络输入变量误差 1 x e = ,误差变 化 2 x e = 。模糊化层节点的激活函数代表模糊变量的隶属函数,该层的权值 ij 表 示隶属函数的形状, c = c 表示隶属函数的位置,该层的输出代表模糊化的结果, 即把确定量转化成了隶属度。模糊规则层将上一层模糊化得到的结果两两相乘, 代表模糊规则的规则强度。将模糊规则层的结果传递给去模糊化层。去模糊化层 的各个权值 代表模糊规则,根据重心法的去模糊化公式,把规则强度加权求和, 输出即为模糊控制器的输出量
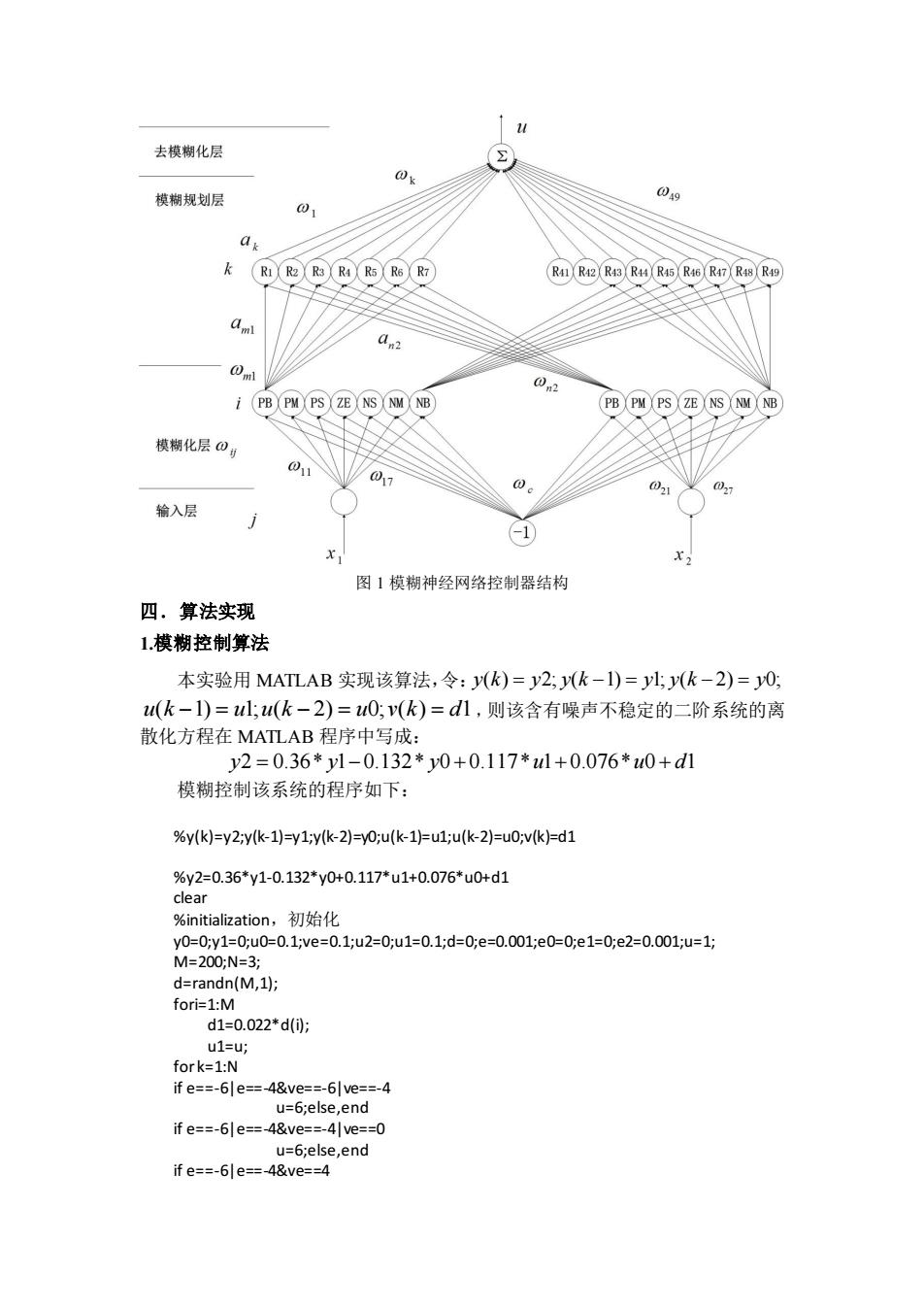
去模糊化层 @k 模糊规划层 09 0 ak (RIR2 R3 R4Rs R6R7 RIR42R43R4R45R46R47R48R49 am an2 Omi 02 i(PB PM PS ZE NS NM NB) (PBPM PS ZENS NM NB 模糊化层0) 011 01 021 07 输入层 图1模糊神经网络控制器结构 四.算法实现 1模糊控制算法 本实验用MATLAB实现该算法,令:y(k)=y2,y(k-1)=yl,y(k-2)=y0; u(k-1)=l;u(k-2)=u0:v(k)=d1,则该含有噪声不稳定的二阶系统的离 散化方程在MATLAB程序中写成: y2=0.36*y1-0.132*y0+0.117*ul+0.076*0+d1 模糊控制该系统的程序如下: %y(k)=y2iyk-1)=y1;yk-2)=y0:u(k-1=u1;u(k-2)=u0v(k)=d1 %y2=0.36*y1-0.132*y0+0.117*u1+0.076*u0+d1 clear %initialization,初始化 y0=0y1=0;u0=0.1ve=0.1;u2=0;u1=0.1;d=0;e=0.001;e0=0;e1=0;e2=0.001;u=1; M=200;N=3; d=randn(M,1); fori=1:M d1=0.022*d(0; u1=u; fork=1:N ife=-6e=-4&ve==-6lve=-4 u=6;else,end ife==-6le=-4&ve==-4|ve==0 u=6;else,end if e==-6|e==-4&ve==4
图 1 模糊神经网络控制器结构 四.算法实现 1.模糊控制算法 本实验用 MATLAB 实现该算法,令:y k y y k y y k y ( ) 2; ( 1) 1; ( 2) 0; = − = − = u k u u k u v k d ( 1) 1; ( 2) 0; ( ) 1 − = − = = ,则该含有噪声不稳定的二阶系统的离 散化方程在 MATLAB 程序中写成: y y y u u d 2 0.36* 1 0.132* 0 0.117* 1 0.076* 0 1 = − + + + 模糊控制该系统的程序如下: %y(k)=y2;y(k-1)=y1;y(k-2)=y0;u(k-1)=u1;u(k-2)=u0;v(k)=d1 %y2=0.36*y1-0.132*y0+0.117*u1+0.076*u0+d1 clear %initialization,初始化 y0=0;y1=0;u0=0.1;ve=0.1;u2=0;u1=0.1;d=0;e=0.001;e0=0;e1=0;e2=0.001;u=1; M=200;N=3; d=randn(M,1); fori=1:M d1=0.022*d(i); u1=u; for k=1:N if e==-6|e==-4&ve==-6|ve==-4 u=6;else,end if e==-6|e==-4&ve==-4|ve==0 u=6;else,end if e==-6|e==-4&ve==4

u=4;else,end if e==-6le==-4&ve==4|ve==6 u=0;else,end ife==-4&ve==-6lve==-4 u=4;else,end ife==-4&ve==-4|ve==0 u=4;else,end ife==-4&ve==4 u=0;else,end ife==-4&ve=4|ve==6 u=-2;else,end if e==0&ve==-6|ve==-4 u=4;else,end ife==0&ve==-2 u=2;else,end if e==0&ve==0 u=0;else,end if e==0&ve==2 u=-2;else,end if e==0&ve==4lve==6 u=-4;else,end ife==2&ve==-6lve==-4 u=2;else,end ife==2&ve==-2 u=0;else,end if e==2&ve==0ve==2 u=-4;else,end if e==2&ve==4|ve==6 u=-4;else,end if e==4|e==6&ve==-6|ve==-4 u=0;else,end ife==4|e==6&ve==-2 u=-4;else,end ife==41e==6&ve=-0 u=-6;else,end ife==4|e==6&ve==4|ve=6 u=-6;else,end u1=u; y2=0.36*y1-0.132*y0+0.117*u1+0.076*u0+d1; y3(0)=y2; up(0)=1; e=(u1/6-y2)*6; e2(0)=e; ve=(e1-e0); ve=round(ve); e=round(e); e0=e1;e1=e;y0=y1;y1=y2;u0=u1; if e<=0.001 break; else end
u=4;else,end if e==-6|e==-4&ve==4|ve==6 u=0;else,end if e==-4&ve==-6|ve==-4 u=4;else,end if e==-4&ve==-4|ve==0 u=4;else,end if e==-4&ve==4 u=0;else,end if e==-4&ve==4|ve==6 u=-2;else,end if e==0&ve==-6|ve==-4 u=4;else,end if e==0&ve==-2 u=2;else,end if e==0&ve==0 u=0;else,end if e==0&ve==2 u=-2;else,end if e==0&ve==4|ve==6 u=-4;else,end if e==2&ve==-6|ve==-4 u=2;else,end if e==2&ve==-2 u=0;else,end if e==2&ve==0|ve==2 u=-4;else,end if e==2&ve==4|ve==6 u=-4;else,end if e==4|e==6&ve==-6|ve==-4 u=0;else,end if e==4|e==6&ve==-2 u=-4;else,end if e==4|e==6&ve==0 u=-6;else,end if e==4|e==6&ve==4|ve==6 u=-6;else,end u1=u; y2=0.36*y1-0.132*y0+0.117*u1+0.076*u0+d1; y3(i)=y2; up(i)=1; e=(u1/6-y2)*6; e2(i)=e; ve=(e1-e0); ve=round(ve); e=round(e); e0=e1;e1=e;y0=y1;y1=y2;u0=u1; if e<=0.001 break; else end

end end M=i; %greapher绘图 i=1:M: subplot(3,1,1) plot(i,up,i,y3,i,y3,'rx") %title('step response of system using FC') xlabel('k'),ylabel('up and y3') legend('up is input','y3 is output'); subplot(3,1,2) e=0.5*(e2/6).2; plot(e) xlabel((k'),ylabel('误差e) subplot(3,1,3) plot(d*0.022) xlabel((k'),ylabel('噪声d) 2.PD控制算法 为了与模糊控制结果进行比较,采用PID控制算法对上述系统进行控制。 根据速度式的PID算式,针对被控系统选取参数,PID算式变为: M=M-0+061-05k-l+01-2a-+ e(k-2) -ek-) 用MATLAB仿真时,上述PID算式可写成: u2=ul+0.06*(1-0.5*el+0.5*(1-2*el+e0)/(1-el) PID控制算法程序如下: clear y0=0y1=0;u0=0;ve=0.1;u2=0;u1=0;d=0;e=0.01;a=0.01;e0=0;e1=0;e2=0.001;u=6;M=200; N=1; d=randn(M,1); fori=1:M d1=0.022*d(0; u1=u/6; fork=1:N u2=u1+0.06*(1-0.5*e1+0.5*(1-2*e1+e0)/1-e1) u0=u1;u1=u2; y2=0.36*y1-0.32*y0+0.71*u1+0.076*u0+d1 y3(0=y2; up(0=1; e=0.5*(u1/6-y2).2; e2(i)=e; ve=(e1-e0); e0=e1;e1=e, y0=y1; y1=y2; if e<=0.001 break;
end end M=i; %greapher 绘图 i=1:M; subplot(3,1,1) plot(i,up,i,y3,i,y3,'rx') %title('step response of system using FC') xlabel('k'),ylabel('up and y3') legend('up is input','y3 is output'); subplot(3,1,2) e=0.5*(e2/6).^2; plot(e) xlabel('k'),ylabel('误差 e') subplot(3,1,3) plot(d*0.022) xlabel('k'),ylabel('噪声 d') 2.PID 控制算法 为了与模糊控制结果进行比较,采用 PID 控制算法对上述系统进行控制。 根据速度式的 PID 算式,针对被控系统选取参数,PID 算式变为: ( 2) ( ) ( 1) 0.06 1 0.5 ( 1) 0.5 1 2 ( 1) 1 ( 1) e k u k u k e k e k e k − = − + − − + − − + − − 用 MATLAB 仿真时,上述 PID 算式可写成: u u e e e e 2 1 0.06*(1 0.5* 1 0.5*(1 2* 1 0) / (1 1)) = + − + − + − PID 控制算法程序如下: clear y0=0;y1=0;u0=0;ve=0.1;u2=0;u1=0;d=0;e=0.01;a=0.01;e0=0;e1=0;e2=0.001;u=6;M=200; N=1; d=randn(M,1); fori=1:M d1=0.022*d(i); u1=u/6; for k=1:N u2=u1+0.06*(1-0.5*e1+0.5*(1-2*e1+e0)/(1-e1)) u0=u1;u1=u2; y2=0.36*y1-0.32*y0+0.71*u1+0.076*u0+d1; y3(i)=y2; up(i)=1; e=0.5*(u1/6-y2).^2; e2(i)=e; ve=(e1-e0); e0=e1;e1=e; y0=y1; y1=y2; if e<=0.001 break;
else end end end M=i %greapher i=1:M; subplot(3,1,1) plot(i,up,i,y3,i,y3,'rx") %title('step response of system') xlabel('k'),ylabel('up and y3) legend('up is system input','y3 is system output'); subplot(3,1,2) plot(e2) xlabel(('k),ylabel('误差e') subplot(3,1,3) plot(d*0.022) xlabel('k',ylabel('噪声d') 五。实验结果: 1模糊控制仿真 模糊控制仿真结果如图2所示。 ☑Figure1 -▣X File Edit View Insert Tools Desktop Window Help 台日始6®⑨9早公,同日国口回 2 up is input y3 is output 号 20406080100120140160 180200 0.4 02 账 20406080100120140160180200 0.1 ythw nh 0. 0 20406080100120140160180200 图2具有噪声的不稳定系统模糊控制结果
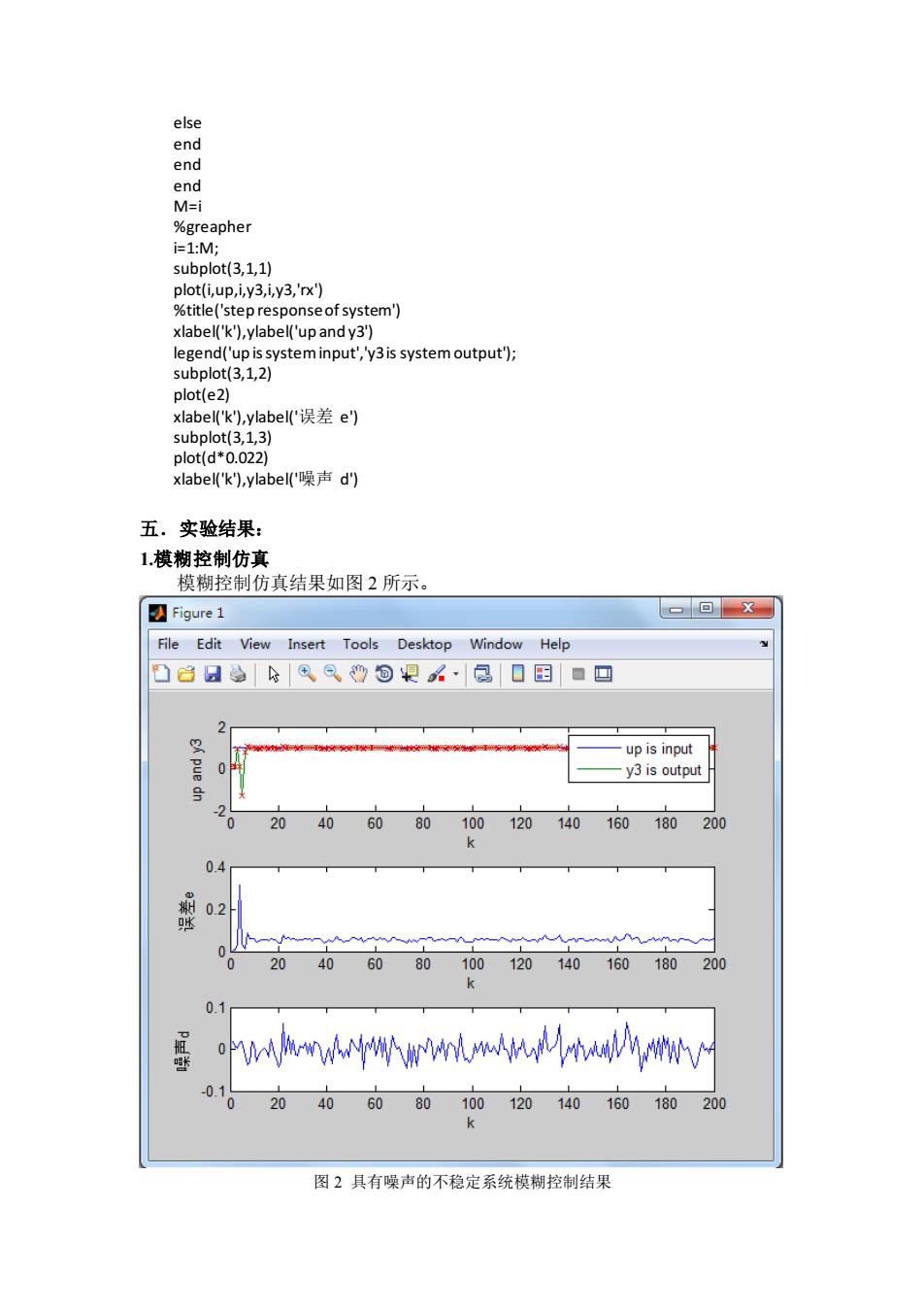
else end end end M=i %greapher i=1:M; subplot(3,1,1) plot(i,up,i,y3,i,y3,'rx') %title('step response of system') xlabel('k'),ylabel('up and y3') legend('up is system input','y3 is system output'); subplot(3,1,2) plot(e2) xlabel('k'),ylabel('误差 e') subplot(3,1,3) plot(d*0.022) xlabel('k'),ylabel('噪声 d') 五.实验结果: 1.模糊控制仿真 模糊控制仿真结果如图 2 所示。 图 2 具有噪声的不稳定系统模糊控制结果

2.PD控制仿真 PID控制仿真结果如图3所示。 ☑Figure1 -回x File Edit View Insert Tools Desktop Window Help 凸启日给®沙回根公易口国■回 15 up is system input pue y3 is system output 号 0. 0 20406080100120140160180200 个 0.5 盥 0 20 406080100120140160 180200 0.1 lmwwmhi人MhMw 0.1 20 4060 80 100 120140 160180 200 图3具有噪声的不稳定系统PID控制结果 六实验总结 经过对比分析实验结果,可以得出以下结论:具有噪声的不稳定系统在使用 模糊控制算法的条件下,系统不断的调整误差,最终使误差控制在5%以内。而 运用常规PID控制器对系统控制的效果要比模糊控制的结果差很多。 由此可见,对于这种具有小噪声的系统,运用模糊控制器进行控制会取得比 传统PID控制更满意的效果
2.PID 控制仿真 PID 控制仿真结果如图 3 所示。 图 3 具有噪声的不稳定系统 PID 控制结果 六.实验总结 经过对比分析实验结果,可以得出以下结论:具有噪声的不稳定系统在使用 模糊控制算法的条件下,系统不断的调整误差,最终使误差控制在 5%以内。而 运用常规 PID 控制器对系统控制的效果要比模糊控制的结果差很多。 由此可见,对于这种具有小噪声的系统,运用模糊控制器进行控制会取得比 传统 PID 控制更满意的效果