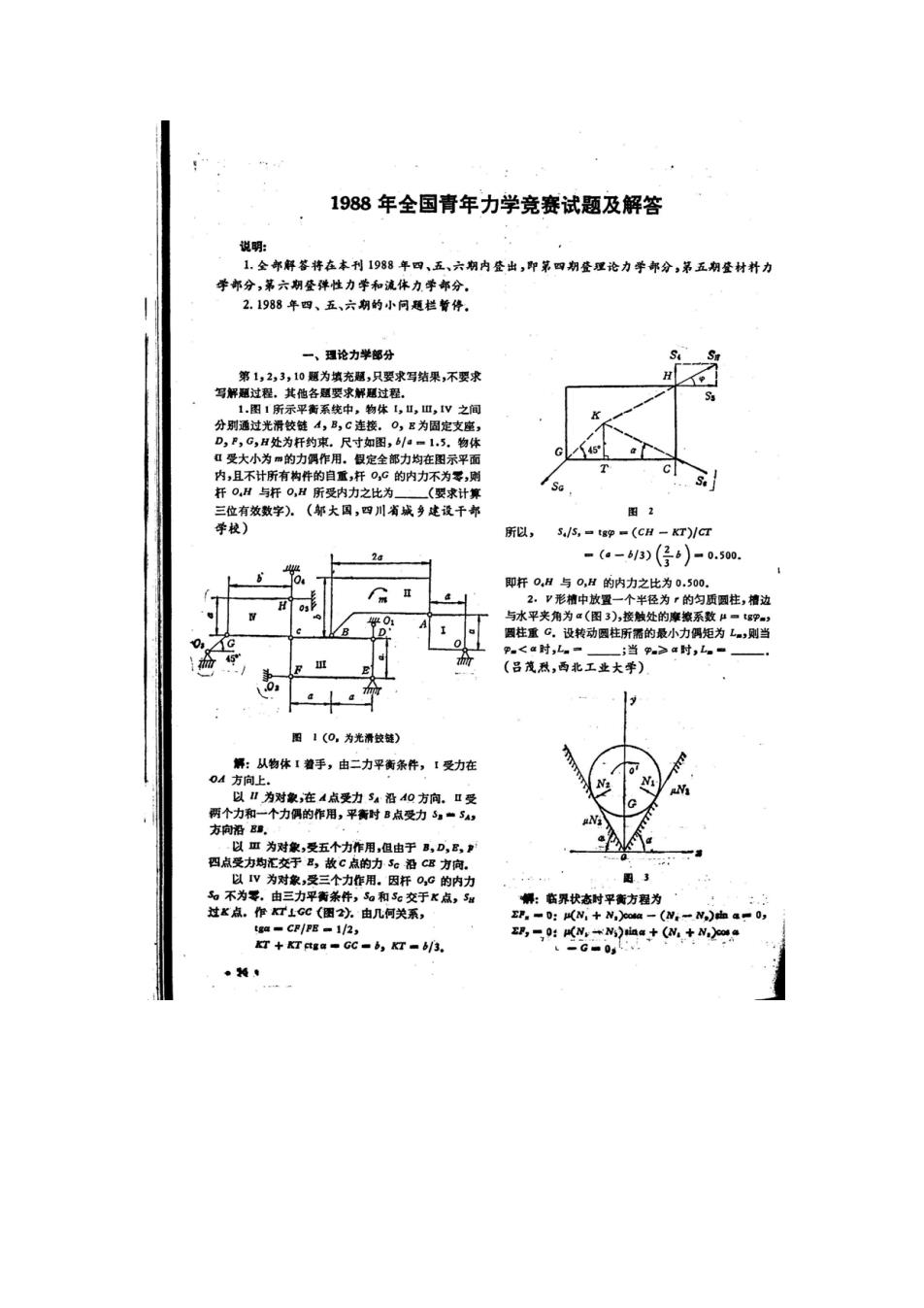
1988年全国青年力学竞赛试题及解答 说明: 1.全部解答将在本刊1988年四、五、六期内登出,即第四期登理论力学部分,第五期登材朴力 学部分,第六期登弹性力学和流体力学部分。 2.1988年四、五、六期的小问题栏箭停. 一、理论力学部分 S 第1,2,3,10题为填充题,只要求写结果,不要求 写解题过程。其他各题要求解题过程, 1.图1所示平衡系统中,物体【,Ⅱ,Ⅲ,V之间 K 分别通过光滑较链4,B,G连接。O,E为固定支座, D,P,G,H处为杆约束.尺寸如图,|a=1.5。物体 Ⅱ受大小为m的力偶作用。假定全部力均在图示平面 内,且不计所有构件的自重,杆0G的内力不为零,则 品 杆O,H与杆O,H所受内力之比为(要求计算 三位有效数字)。(邬大国,四川省城乡建设干部 图2 学校) 所以, /S,tgp -(CH -KT)/CT 24 -a-61)(径0)-0.50. 0 即杆O,H与O,H的内力之比为0,500, 2,V形槽中放置一个半径为?的匀质圆柱,槽边 9 与水平夹角为✉(图3),接触处的摩擦系数肚一gP, 國柱重G,设转动圆柱所需的最小力网矩为L。,则当 0 G p。<时,La=一;当≥a时,。= (吕茂烈,西北工业大学) 0 图1(0,为光滑饺链) 解:从物体1着手,由二力平衡条件,【受力在 0A方向上. N 以Ⅱ为对象,在4点受力Sa沿0方向。Ⅱ受 两个力和一个力偶的作用,平衡时B点受力5“5, 方向沿■。 以亚为对象,受五个力作用,但由于8,D,B,P 四点受力均汇交于B,故C点的力5c沿CB方向。 以W为对象,受三个力作用。因杆O,G的内力 图.3 g不为零.由三力平衡条件,5o和5c交于x点,5 解:临界状态时平衡方程为 过x点.作口1GC(图2功.由几何关系, EF.0:H(N,N,)coa-(Ni-N)gin a03 tga-CF/PE -1/2, z现,=0:以N,*y)恤a+(WtN,94 r+KT ctga●GCb,T■/3. -G0
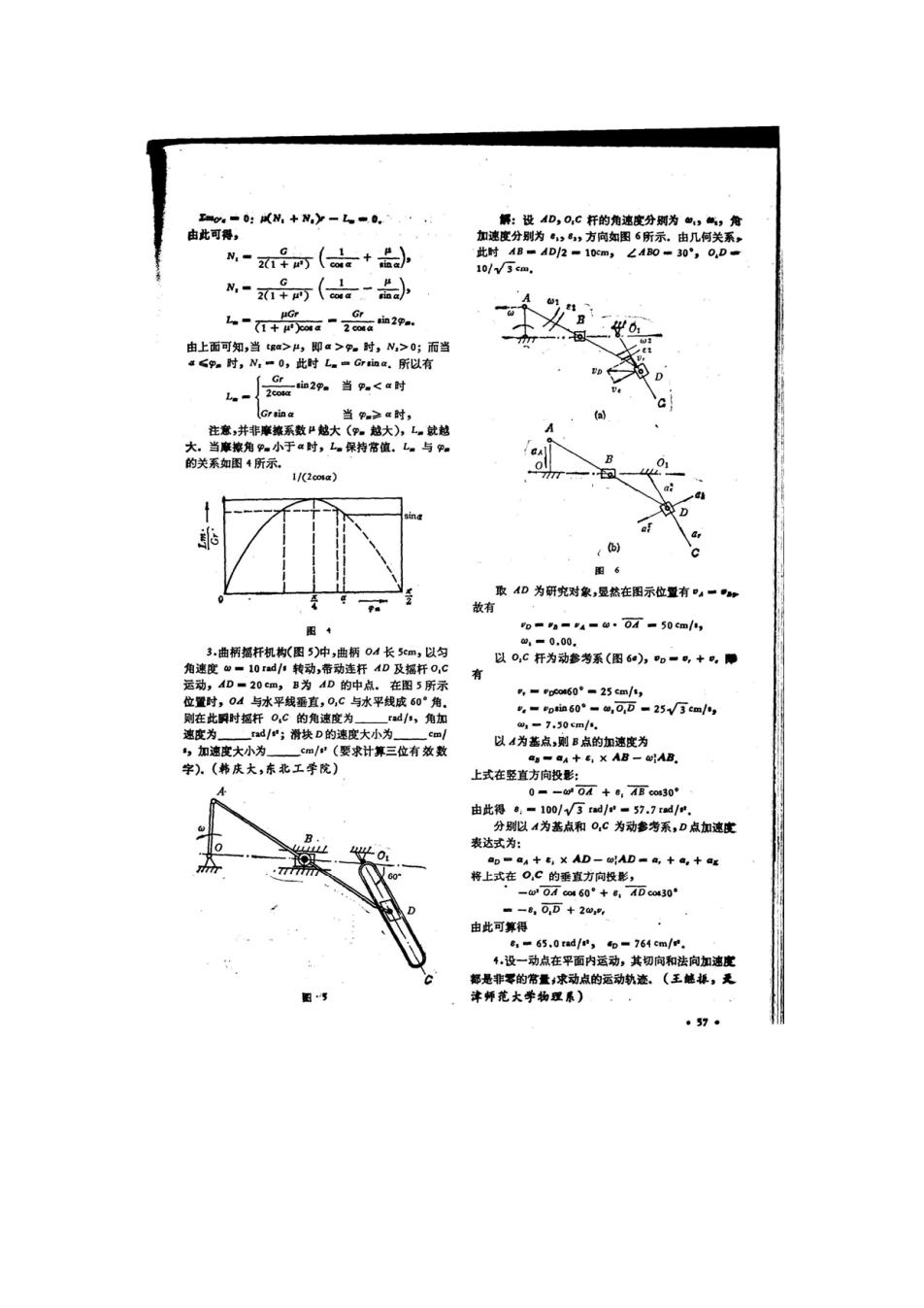
a=0:风N,+N,)y-L。=0. 解:设4D,0,C杆的角速度分别为,气,角 由此可得, 加速度分别为,8,方向如图6所示。由几何关系, M-时(品女t品)》 此时AB=AD/2=10cm,∠A0=30°,0,D- 10/√3cm Ma可(-》 人“+-z8。m 由上面可知,当ga>4,即a>。时,N,>0;而当 &≤Pa时,N,=0,此时L。=Gr sin a。所以有 _Gri血2p.当.<a时 Le- 2cota Grsina 当≥a时, 注意,并非摩擦系数“越大(。越大),L。就越 大。当摩擦角P。小于a时,L。保持常值.L。与p。 的关系如图4所示. 1/(2co4a) 图6 取AD为研究对象,显然在图示位量有·a一 故有 0-a-4-0.0i-50cm, 1=0.00. 3.曲柄摇杆机构(图5)冲,曲柄04长5cm,以匀 以0,C杆为动参考系(图6@),o=,+”,雕 角速度■10rade转动,希动连杆AD及摇杆O,C 有 运动,AD=20cm,B为AD的中点。在图5所示 ,=Peeo60°=25cm/, 位置时,04与水平线垂直,0,C与水平线成60°角. -pim60°-m,0D-25V/万cm, 则在此明时超杆O,C的角速度为 rad/小,角加 01=7,50cm/. 速度为 rad/:;滑块D的速度大小为 cm/ 以A为基点,则B点的加速度为 ,加速度大小为 一cm/:(要求计算三位有效数 as-a+x AB-@AB. 字)。(韩庆大,东北工学院) 上式在竖直方向投影: 0=-0M+8,ABco430° 由此得,-100/√了radr-57.7rd/r 分别以4为基点和0c为动参考系,D点加速度 表达式为: ap=aA+×D-oAD=a,+高,+ag 将上式在O,C的垂直方向投影, -w0icas60°+8,ADco430° =-,0,D+2w,, 由此可算得 6,=65.0ad/,o=764cm/. ,设一动点在平面内运动,其切向和法向加速度 都是非零的常量,求动点的运动轨迹。(王触渠,更 津师范大学物理景) ·57

解:由已知条件, 静止,今小虫突然以相对速度“(常量)沿杆向B来动 4名名如 (图).试写出杆与地面夹角:所满足的微分方程及 初条件。(或斐,救金生,北京大学) 台碧 G1 设青一,(c,),则 名片名-台北 积分上式,得一的,从而有 -0-系w0, 又, -nag-名x.a, 图8 解:(1)初始时为冲击过程(图9). y-m0-a新em00 ()设,0,1,年0,水平方向和竖直方向的漏 积分得,一 量方程为 -1)+血)+n e ’。0+可(2t9-ea0)+n 适当速取坐标系,总可使,一,■0。选取极坐 标系(图7),极角p一日一4,极轴 ,-√+7-,w+了 - tga-tg(8-p)-- 所以。一常数 图 +一常量, 10 就有 :. 即动点的轨遗为对数爆线。 ≥5.员量为细的杆48斜靠在竖直维上,A绮有一 小虫,其质量也为m。撞和地面都是光清的。原系线 。物

其中1为杆长,相对于“固定点”(与4端重合的点)A 设系统质心:的坐标为()(图9),则 的动量矩方程 P 2mc N-2mg -2mye 12 -N(lcosa-)P(Itina-e) -《+业- 运动学关系, -,+7o抽a-0 +[侣+侣-“门} ,-aa-0. 系.-u+2coa, 2 联立求解上述五个方程,得 -(-)ma-(层-》m 的m3 in acosa/[(1+3coe'a)】, =3usin'acosa/[2(1 +3cos'a)], 由此可得运动微分方程为 =3usin acos'a/[2(1 3cos'a)]3 en-2cara+(侵+cor a)p]a 1.musin a(3cos'a -2)/[2(1 3cos'a)], +(2ut-Ia sin acosa l4=mcosc(9co2a-1)/八2(1+30o3a)】. +2(u-1 cos")wd 此时应有1,≥0,,≥0,故初始时应有 aso胥: +(u-是)aa-0 初条件为 (b)1,=0,1,年0(图9b),与上面相似,可列出 三个动力学方程和两个运动学方程: --√写。可用 P=2mi3 一2mR一2m成。(此方程可用来检查B端是否 碰地) -专oaa-0, m,a-[g(au-y+立} 与-子cw20. 2wl co a. 4 由前四个方程可解得: w=6usin acosa/[1(8 -3cos'a)], 最后得运动微分方程, 3usin'acosa/(8-3cos'a), [n(1+e)-eawa+合6+3aa]小a :=usina(4-3cos'a)/(8-3cos'a), I,-5mu cos a/(8-3cos'a). +号(2m+y恤acoa 考虑到第五个方程后,可得初始时应有 [2ur(1 sin'a)-Icos'a ]ud =0. >a√写, 初条件为 (c)其他情形. a-a>r√写, -山-0,当且仅当0-受时才会发生,这已 l=6usin as cosae/[K(8 -3cos ae)]. 包含在()中. 6.一质量为M,半径为6的空心薄圆柱O,在光 1,车0,1,=0,因>0,且沿AB方向,这种情 滑水平面上运动,另一质量为m,半径为(<b)的空 况是不可能发生的。 心薄圆柱O,在圆柱O,的内表面作纯激动(图10), (2)根据前面的分析,可分两种情形讨论。 令日角为O,O,与向下竖直线的夹角。设初始时静止; 0初始时a<um√胥. 且9一月,试写出运动过程中日与日的关系式。(程 稼夫,中国科枝大学) +594

+告(a+e+a6-d +m(6-a8+m[b-(b-aoa9] 10 -常量=m[6-(B一os] 将,中的表达式代人即得 -·品(e- 7 7,若在地球表面上4,B两点间打通一条光滑隧 图16 道,质点m从4点由静止开始,借地心引力落人隧道. 解:设0(x,b,0(,),则 在地球内部地心引力取F一一受,:为地球表面 1=x,+(b-c)sin0, 的重力加速度,R为地球半径,不计地球自转的影响。 %▣b-(6-aos9, ()当4A,B间隧道为直线时(图12),求质点从 动能 T=吉M+之Mb A到B的时间. ()当隧道为ACB折线时,求A到B的最短时 +之(纠+功+之mn 间及最优折线。 (©)求A到B的最短时间及最优隧道的形状. 势能 V=m21 纯滚动条件:(日+p)=(日+). (吕茂烈,西北工业大学) 系统有三个自由度,取广义坐标为x,8,伞(图11). 系统的Lagrange函数为 L-之(w+m)用+nm(b-0eat0 +宁w+m沙+5-0 +m(b-a)a-mg[b-(8-a)cos0]. 图12 解:()设0,为坐标原点,0,B为¥轴,质点 0,点x(图13),则R=一m/R一m,解得 00 -m√ 0 运动周期T-2所,故从4到B的时间为√图, 图11 约42,2分钟。 由Lagrange方程,考虑初条件,‘▣0时,文,=6一 p=0,日=B,得 8L 所, -(M+m)共,+m(5-a)0cos0-常量=0, 的=(4+mp+m6(8-)9-常量=0. OL 所以 --n十6-)ico明 图13 净-平n,20 6 ()以O,为坐标原点,O,B为x轴,质点距A 显然总机械脂守恒,“十 点为.利用()的结果及对称性,在4C段有 r+p-2a+如g+n(6-gcog -受m√受, 60

设质点由4到c的时间为c,则有 这是经典的泛函极值问题,p满足Buler-Lagrange方 c-吉和-支而@(N贯) 程: -款e). -R(0+[1-a(√贯小 因。不显含8,故存在初积分 花-夜c高-R血(94+) -r架-6 -Rcod(8+8)tgoj 在一p处,P一0,可确定积分常数C,由此可 所以k-√.·ra[a(0+ya] 得 由6c/09■0,得 +-台(二) im2(e,+0)-m20-0 由对称性,可只考患>0(>0),得 或 co20+0a)in94=0. 因日4年0,故最大倾角(即最忧折线之夹角∠B4C) 0-常√哥 .--2 积分后 质点通过最优折线之时间(最短时间)为 0-w√二 -%.-2√里ew+82 -√g,o (c)取极轴0P⊥4B(图14,图中9,+8,=0), 势能()=m/(2R),由能量守恒, 这是圆内旋轮线方程(图14),当,一R,日=日。时, 可得 之…+紧, 。-1-9)风 得质点速度为 -√/R-7R. 质点由4经旋轮线到B的时间(最短时间)为 m-2√g·,0 -2·2 -√, rdr ‘7-PX0-可 -√2”去 图14 -·√P-2Wa-. R& 因-仙,且 下面说明方程(*)是圆内旋轮线方程,由图14, d山-√(ry+(0莎-√+F,0 0,R=2ba(b是小圆半径),即 其中=rld8,故有 -女√马 设R=2b+P,即2b=R-p,2(R-b)=R+P, 在△OM5中, 令 ,-√5, rR+(2bcota)-2R.2bcos'a 即2b.2(R-boa--A 则有 -√臣· 所秘m√舌,√哥

是在dOMg中,·对 8+a++受-即0,-(货-)-✉ 又因为 血位+兴 所以 恤-ma-√二F, (传-)--√二 图16. 将碰撞后的△OAB与点P的位形相对碰撞壁AB作 最后 镜面反射(图17),则点P碰撞前后的轨迹仍连接成一 -8+8-费+(侣-心)-4 直线,速度保持不变。 -(倍-) √二 会√二g. 图17 8.质量均为m的两质点P,P,沿一光滑直线Ox 图18中有阴影的三角形表示经反射后和原来的 运动,其位置在距离为,的两壁之问(图15),设质点 △OAB一致的三角形。点P运动到阴影三角形中相同 之间,质点和墙壁之间的碰撞都是完全弹性的。问在 位置的P时,表示两质点P,P,回到了初始状态,此 什么条件下,经过一段时间后,两质点的位置和速度同 时两著的坐标差为 时回到初始状态?若发生两质点同时与一侧壁碰撞的 △r.=2(m+n),△r,=2l. 三体碰撞时,则视为无限短时间内相继发生的两体碰 由图16,两质点的速度比为 撞。(胡守信,吉林大学) 这表明质点组作周期运动的必要条件是它们的速度比 ,/知,为有理数(m,a为整数),包括比值为∞(”,=0) 和0(·,一0),与质点组的初始位置无关,不难说明 这一条件也是充分的, 图15 解:以质点P,,在Ox轴上的坐标,,作为 平面0r,而中一点P的坐标(x,x,),这样,质点组 P,P,的位置和速度可由点P在坐标系中的位置和速 度表示(图16). 因0≤,≤,≤,故P点限制在△0AB中运动」 点P与O4边、AB边和OB边的碰撞,实际上分别 :是质点户,与左壁,质点月与右壁以及两质点之间的 碰撞。因碰撞是完全弹性的,故质点与壁碰撞时速度 反向,P,与P,碰撒后交换速度,所以,对应的P点的 碰撞是相对OA,OB和4B的完全弹性反射,没有 碰撞时和为常数,对应于P点轨迹为直线.以 2时 点P与4B边碰撞为例(即质点P,与右壁碰撞),若 2…

9,半径为,质量为m的均匀圆球在半径为6的 dcosB,0=&sinB(7) 完全粗德的另一围定圆球的外表面上浓动,试建立动 ,e,=(e+b)d,a=,-(a+b)co4p, 球的运动微分方程。当动球转速超过多少时,动球可 a=0、 (8) 以在定球的最高点处稳定地转动。(出题者:程稼 约束条件: 夫,中国科技大学解题者:费书悬,清华大学) ,=:十×(一4,)▣0 ,-4=0,"a十m,=0 -Taoon, m,-g-‘+上6 《9) 将(),(9)代入(6)得到关于自转角速度, 的特性。 ⊙,0,或 的,-常数·(10) 将(7),(8),(9)代人(1),(2),(4),(5)得: m(a+bB+'cos6in月 =F,十mgcosa sin B (11) m(a +bX-acos8 2dgsinB) 0 eF,一mgsi面a (12) 子n(+bXa明-2的) +号a- (13) 号n(+bXa+rcap) 图19 (14) 解:本题中动球受非完整约束,故不能应用拉氏 二类方程;又因要求动球在最高点处转动的稳定条件, 从上面四式中消去术,F,即得动球的运动微分方程 所以也不能用球坐标描述球心的位置,如图19所示, 式: 用卡尔丹角4,B描述动球质心C的位置;建立动坐标 7(a)(ico-2dsinB)+2 系Ox,它相对定坐标系的方位由a,P确定,其角速 -5gsina0 (15) 度为口.坐标系[C,一,】过动球质心C,且与 7(a +68+i sin Bcoep)-2a0,dco 坐标系Oy相平行,动球质心C的速度为”,动球 5gcosasinB=0 (16) 绝对角速度为。动球所受之力为m,N,F,F,。 此方程有特解a”一0,一0,代表动球在固定球的 由质心运动定理向动坐标系Oy:各轴的投影式 最高点处以,自旋的运动。为研究此运动的稳定性, 得: 将4,A看成小量,并在式(15),(16)中略去二阶以上 m(-+De)-F+mgcosasinB (1) 的小量,得到线性化的受扰运动方程: m(e,-0ea十0ee)=F,一mg血a 7(a+b)定+2a9-5ga■0 (2)》 (17) m(+)-N mgcosacos8 (3) 7(a+B)8-2a0d-5g8-0 (18) 由相对质心的动量矩定理在动坐标系【C,一,, 其特征方程为: ,】各轴的投影式得: 17(e+b)从-5e 2a0, A(1)= =0 子(a,-a,+,o)-Pn 4) -24001 7(a+b)-5g 或 49(a+b2+[ea鲥-70(a+b)g] 子n(a-0@+0o)--0”(5) +25g=0 《1財 四个特征根都没设有正实部的条件是:· 子n(,-0,m+0,e)-0 (6) [4-70(e+6)g小-4·25·49a+ by≥0 (20) 运动学关系: a≥35g(a+b6)/d .-0x(a+b% (21) 这就是动球在最高点自转运动的稳定条件(严格地讲, 。g

“这样求得的只是稳定的必要条件).。1 10,内半径R一30cm的空心圆柱0,水平固定 (0)-8(4+2mw) (放置.质量为M,半径为,一10cm的均匀圆环0 可以在圆柱内作纯滚动.质量为m的质点4固联在圆 势能为 环0,的边缘上,当圆环0,处于圆柱0的最低位置 v- -Mg(R-r)cos8-mg(R-r)cos0 +mgro 时,质点4处于圆环的最高位置.设00,与向下竖直 -2(M+m)grcos migrcos20, 线的夹角为0(图20).则,当M=2m时,圆环的稳 V'2(M+m)grsin8-2mgrsin20 定的平衡位置为日■ 二弧度,圆环在此平衡位置 2gr[(Mm)iin-msin20] 附近微振动的周期为秒;当m一2“时,圆环 v"=2gr[(M+m)cos0-2mc0s20] 的稳定的平衡位置为日一 由P”-0,即 一弧度,圆环在此平衡 位置附近微振动的周期为 秒(取重力加速度 i[(M+m)-2eos8]=0 。一980屈米/秒,要求计算三位有效数字).(散全 求得两个平衡位置: 生,北京大学分校,武斐,北京大学) (a)6=0.=0,由Vl。。=2r(M-m)3 M≥m时,0一0为稳定的平衡位置,当Mm时,圆环的稳定的平衡位] (R-)0=网 为0=0.00弧度.此时,(0)=8(M+2m)P=3 由题意,R一3一30cm,故有-28.系统动能 m,V”(0)一2rm,所以微报动周期 K-()型+M(y -√隔-√g =2.54秒. +宁m安ヅ ()当m一2M>M时,國环的稳定的平衡位里 为 -wr0 wboe碧-o0 0-0,-are coM+-are c-0.7233孤度. 2m 此时 《0,)-8(u+2mco号)r -8wr(+4aw是小 微振动周期 图21 -a√隔 6(+e是 其中 ■1.32秒。 拉于道 认44。)、口… 。4