
74 力学与实 2000年第22卷 第四届全国周培源大学生力学竞赛材料力学试题 题-(25分) 题三(20分) 如图所示,狭长矩形截面直杆单侧作用有轴向均 矩形等截面悬臂梁高五宽6,长1.重Q的重 布剪切载荷,其单位长度上的大小为? 物从高H=60Q2 处落到自由端并附着于它.梁的 质量不计,E为材料的弹性模量,I为截面轴惯性 矩 1. (5分)梁内最大神击正应力od,max= 将梁设计成两段等长的阶梯梁(两段各长/2), 图1 粱高力保持不变,各段粱宽度可按要求设计,在梁内 1.(5分)任意截面上的轴力V(x)= 最大冲击正应力不变的条件下,按最省材料原则,阶 与弯矩I(x)= 梯梁在靠自由端一段宽1,靠周定端一段宽2,则 2.(5分)如果平面假设与胡克定律成立,任意 2.(5分)b1/b2= 横截面上正应力σ(红,)= 3.(10分)阶梯梁比等截面梁节省材料(分数或 3.(5分)q、N与M之间的平衡微分关系为 百分数表示) 题四(15分) 4. (10分)任意横裁面上剪应力r(x,)= 如图所示,简支梁AB承受均布载荷,在C, D两点的两个相等的集中力P,在B点的集中力偶 题二(20分) M的作用. U是梁的应变余能(线弹性情形下等于 今有两个相同的L型元件,用螺栓连接,以传递 应变能) 拉力P,几何尺寸如图所示.L型元件是刚体,螺栓 P P 是线性弹性体,其拉压弹性模量为E,许用正应力为 [a]. B C D 2c -M 图3 U 1.(5分) OMT 的几何意义为 2.(5分) 的几何意义为 OU 3.(5分) OU 0q 的几何意义为 图2 题五(20分) 设两L型元件间无初始间欧,也无预紧力,并设 曲杆AB的轴线是半径为R的四分之一圆弧, 在变形过程中两个螺母与L型元件始终贴合,螺栓与 杆的横根面是直径为d的实心圆,d<<R,杆的A 工型元件在孔壁何无相互作用力,则 端周定,B端自由,并在B端作用有垂直于杆轴线 1.(5分)在工型元件孔内一段螺栓的轴力 所在平面的集中力P.已知材料的拉压弹性模量E、 N= 剪切弹性模量G与许用拉应力σ 2.(⑤分)在工型元件孔内一段螺栓的弯矩 1.(10分)按第三强度理论,许用载荷[月= M= 3.(5分)两个L型元件相对转角△6= 2.(10分)在载荷P的作用下,自由端绕杆轴 线的转角BB= 4.(5分)许用拉力[可
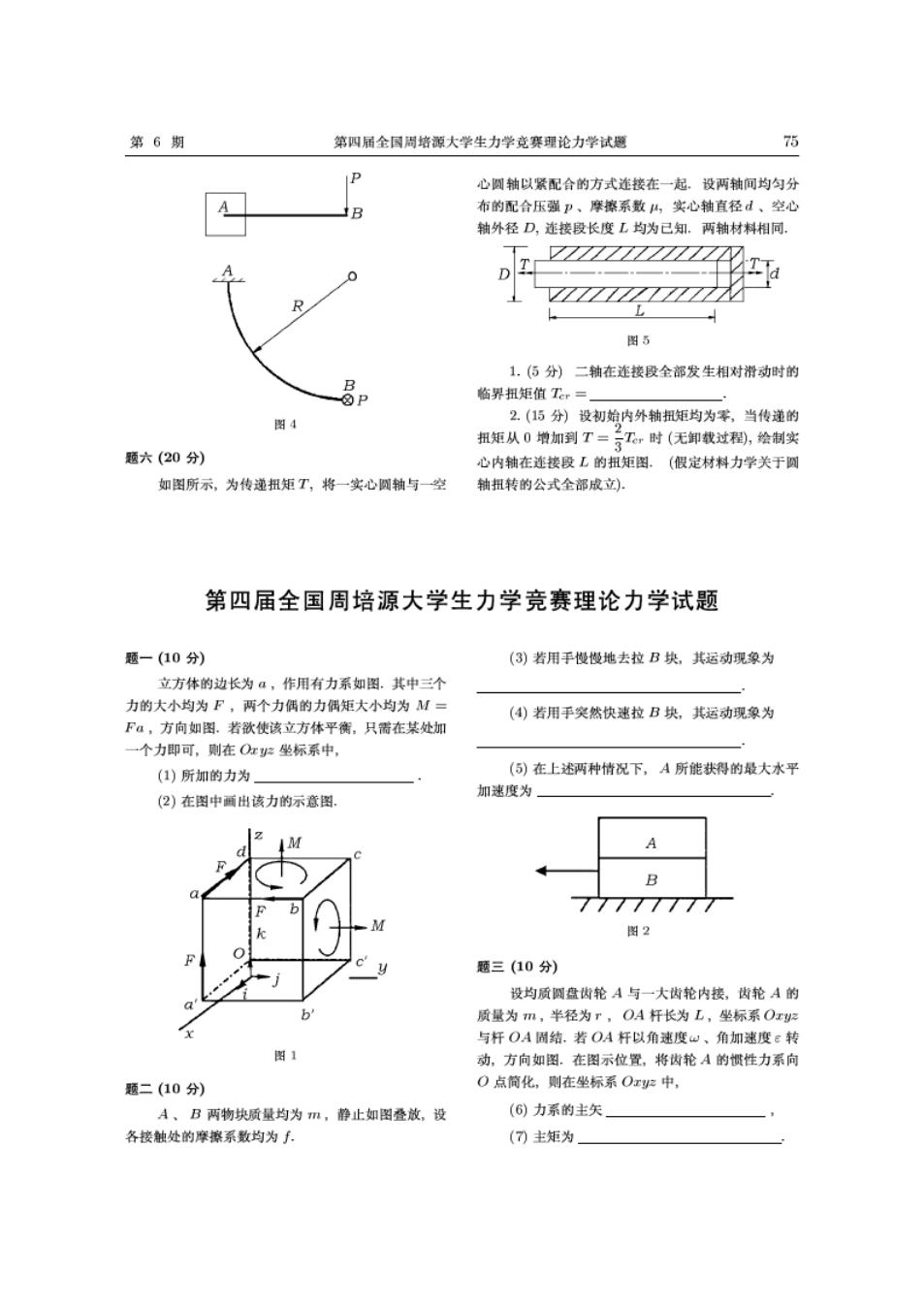
第6期 第四届全同周培源大学生力学竞赛理论力学试题 75 P 心圆轴以紧配合的方式连接在一起.设两轴间均匀分 B 布的配合压强p、摩擦系数山,实心轴直径d、空心 轴外径D,连接段长度L均为已知.两轴材料相同 0 图5 1.(5分)二轴在连接段全部发生相对滑动时的 B 因P 临界扭矩值Tr= 图4 2.(15分)设初始内外轴扭矩均为零,当传递的 扭矩从0增加到T=亏,时(无卸载过程),绘制实 题六(20分) 心内轴在连接段L的扭矩图.(假定材料力学关于圆 如图所示,为传递扭矩T,将一实心圆轴与一空 轴扭转的公式全部成立): 第四届全国周培源大学生力学竞赛理论力学试题 题-(10分) (3)若用手慢慢地去拉B块,其运动现象为 立方体的边长为a,作用有力系如图.其中三个 力的大小均为F,两个力偶的力偶矩大小均为M (4)若用手突然快速拉B块,其运动现象为 Fa,方向如图.若欲使该立方体平衡,只需在某处加 一个力即可,则在O:2坐标系中, (1)所加的力为 (5)在上述两种情况下,A所能获得的最大水平 加速度为 (2)在图中画出该力的示意图, y B 7777777 图2 题三(10分) 设均质圆盘齿轮A与一大齿轮内接,齿轮A的 b 质量为m,半径为r,OA杆长为L,坐标系Ox2 与杆OA圃结.若OA杆以角速度、角加速度e转 图1 动,方向如图。在图示位置,将齿轮A的惯性力系向 题二(10分) O点简化,则在坐标系Ox中, A、B两物块质量均为m,静止如图叠放,设 (6)力系的主矢】 各接触处的摩擦系数均为子. (7)主矩为
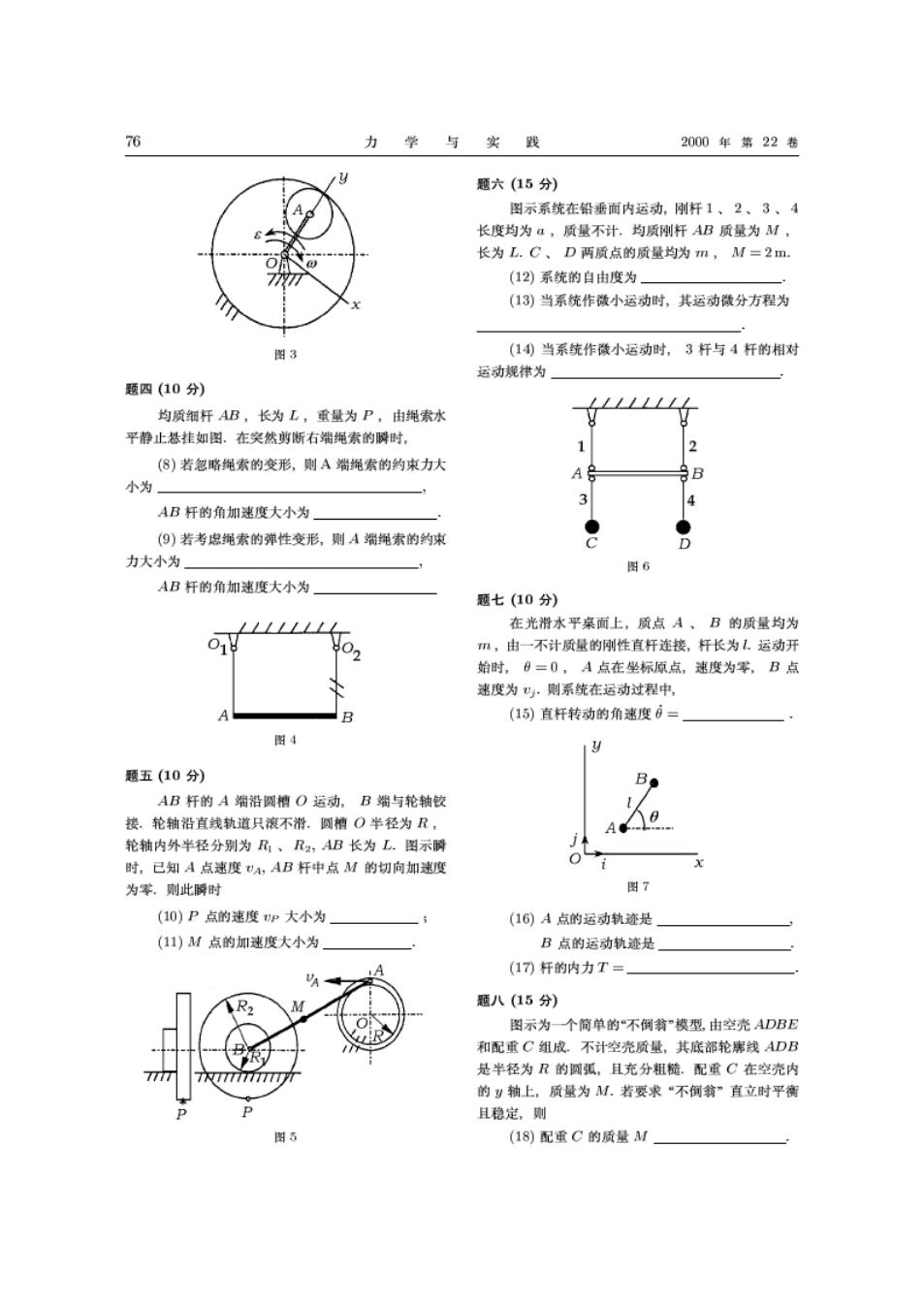
76 力学与实 2000年第22卷 题六(15分) 图示系统在铅垂面内运动,刚杆1、2、3、4 长度均为a,质量不计.均质刚杆AB质量为M, 长为L.C、D两质点的质量均为m,M=2m (12)系统的自由度为 (13)当系统作微小运动时,其运动微分方程为 图3 (14)当系统作微小运动时,3杆与4杆的相对 运动规律为 题四(10分) 均质细杆AB,长为L,重量为P,由绳索水 平静止悬挂如图。在突然剪断右端绳索的瞬时, (⑧)若忽略绳索的变形,则A端绳索的约束力大 小为 AB杆的角加速度大小为 (⑨)若考虑绳索的弹性变形,则A猫绳索的约束 力大小为 图6 AB杆的角加速度大小为 题七(10分) 在光滑水平桌面上,质点A、B的质量均为 m,由一不计质量的刚性直杆连接,杆长为1,运动开 始时,0=0,A点在坐标原点,速度为零,B点 速度为巴,则系统在运动过程中, B (1)直杆转动的角速度6= 图4 题五(10分) AB杆的A端沿圆槽O运动,B端与轮轴皎 接.轮轴沿直线轨道只滚不滑.圆槽O半径为R, 轮轴内外半径分别为B、R2,AB长为L.图示瞬 时,已知A点速度A,AB杆中点M的切向加速度 为军。则此瞬时 图7 (10)P点的速度vP大小为 (16)A点的运动轨迹是 (11)M点的加速度大小为 B点的运动轨迹是 A (17)杆的内力T= R 题八(15分) 图示为一个简单的“不倒翁”模型由空壳ADBE 和配重C组成。不计空壳质量,其底部轮廓线ADB 是半径为R的圆弧,且充分粗髓.配重C在空壳内 N7777777777 的y轴上,质量为M.若要求“不倒翰”直立时平衡 且稳定,则 图5 (18)配重C的质量M

第6期 第四届全同周培源大学生力学竞赛理论力学试题 77 (a)越大越好:(b)越小越好:(c)可为任意值 题九(10分) (d条件不铭不能确定 设Oxy2为参考坐标系,矩形板(三角形为其上 (19)配重C的位置范围 的标志)可绕O点作定点运动.为了使矩形板从状态 y 1创z平面内)运动到状态2(xy平面内肉),根据欧拉 E 转动定理,该转动可绕某根轴的一次转动实现,则在 Oxyz坐标系中 (21)该转轴的单位矢量 (22)转角为 R◆C D 图8 (20)若已知M、R、OC=d,则模型微摆 动的周期 图9