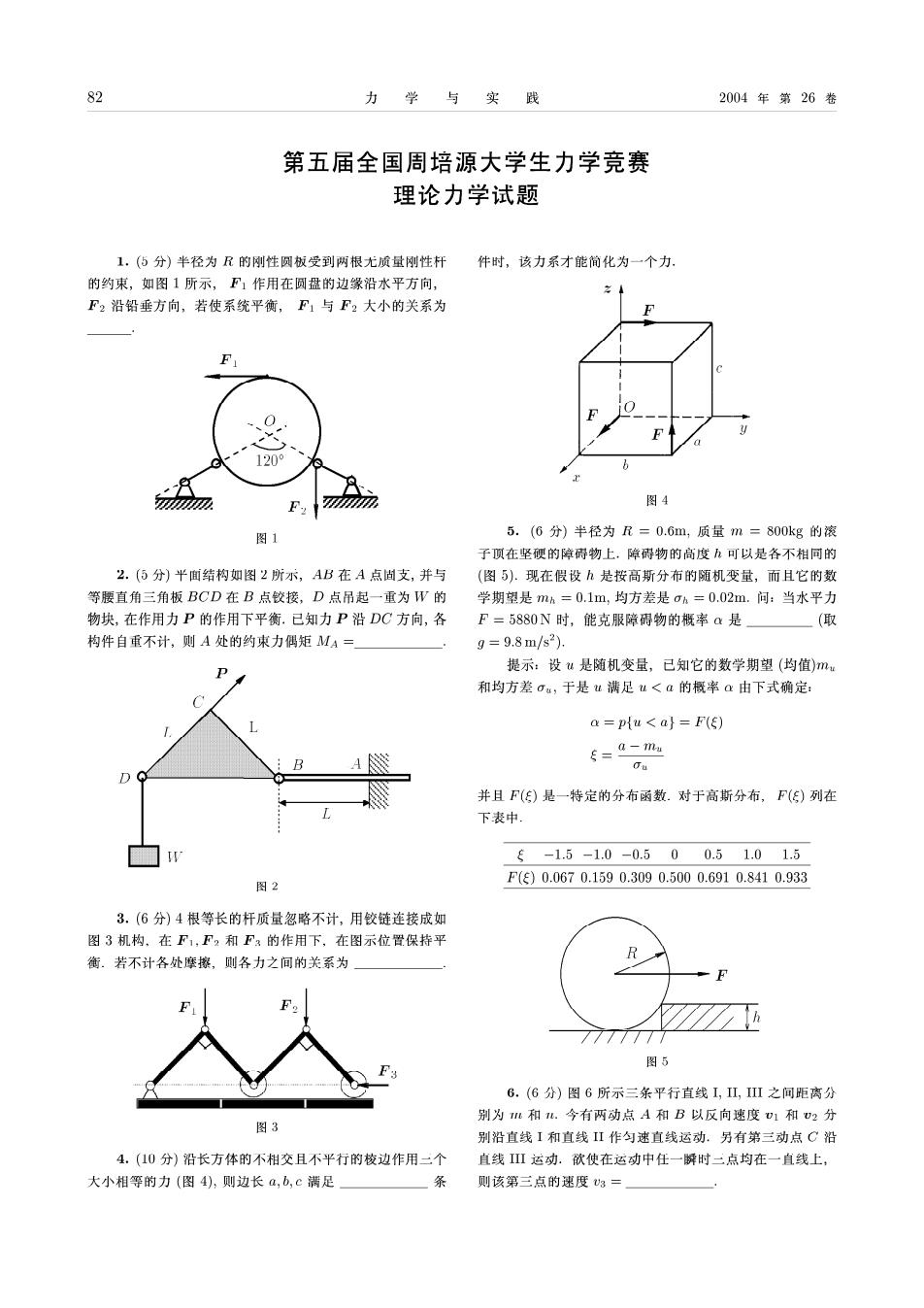
82 力学与实践 2004年第26卷 第五届全国周培源大学生力学竞赛 理论力学试题 1.(5分)半径为R的刚性圆板受到两根尤质量刚性杆 件时,该力系才能简化为一个力. 的约束,如图1所示,F1作用在圆盘的边缘沿水平方向, F2沿铅垂方向,若使系统平衡,F1与F2大小的关系为 120° 图4 图1 5.(6分)半径为R=0.6m,质量m=800kg的滚 子顶在坚硬的障碍物上,障碍物的高度可以是各不相同的 2.(⑤分)平面结构如图2所示,AB在A点卤支,并与 (图5).现在假设h是按高斯分布的随机变量,而且它的数 等腰直角三角板BCD在B点较接,D点吊起一重为W的 学期望是mh=0.1m,均方差是oh=0.02m.问:当水平力 物块,在作用力P的作用下平衡.已知力P沿DC方向,各 F=5880N时,能克服障碍物的概率a是 (取 构件自重不计,则A处的约束力偶矩MA= g=9.8m/s2). P 提示:设u是随机变量,已知它的数学期望(均值)mu 和均方差ou,于是u满足u<a的概率a由下式确定: C a=p{u<a}=F(ξ) B 5=0-mu D 并且F()是一特定的分布函数.对于高斯分布,F()列在 下表中 ξ-1.5-1.0-0.500.51.01.5 图2 F(E)0.0670.1590.3090.5000.6910.8410.933 3.(6分)4根等长的杆质量忽略不计,用铰链连接成如 图3机构,在F1,F2和F?的作用下,在图示位置保持平 衡.若不计各处摩擦,则各力之间的关系为 F. 图5 6.(6分)图6所示三条平行直线I,II,III之间距离分 别为和1.今有两动点A和B以反向速度1和v2分 图3 别沿直线I和直线II作匀速直线运动.另有第三动点C沿 4.(10分)沿长方体的不相交且不平行的棱边作用二个 直线Ⅱ运动.欲使在运动中任一瞬时二点均在一直线上, 大小相等的力(图4),则边长a,b,c满足 条 则该第三点的速度3=
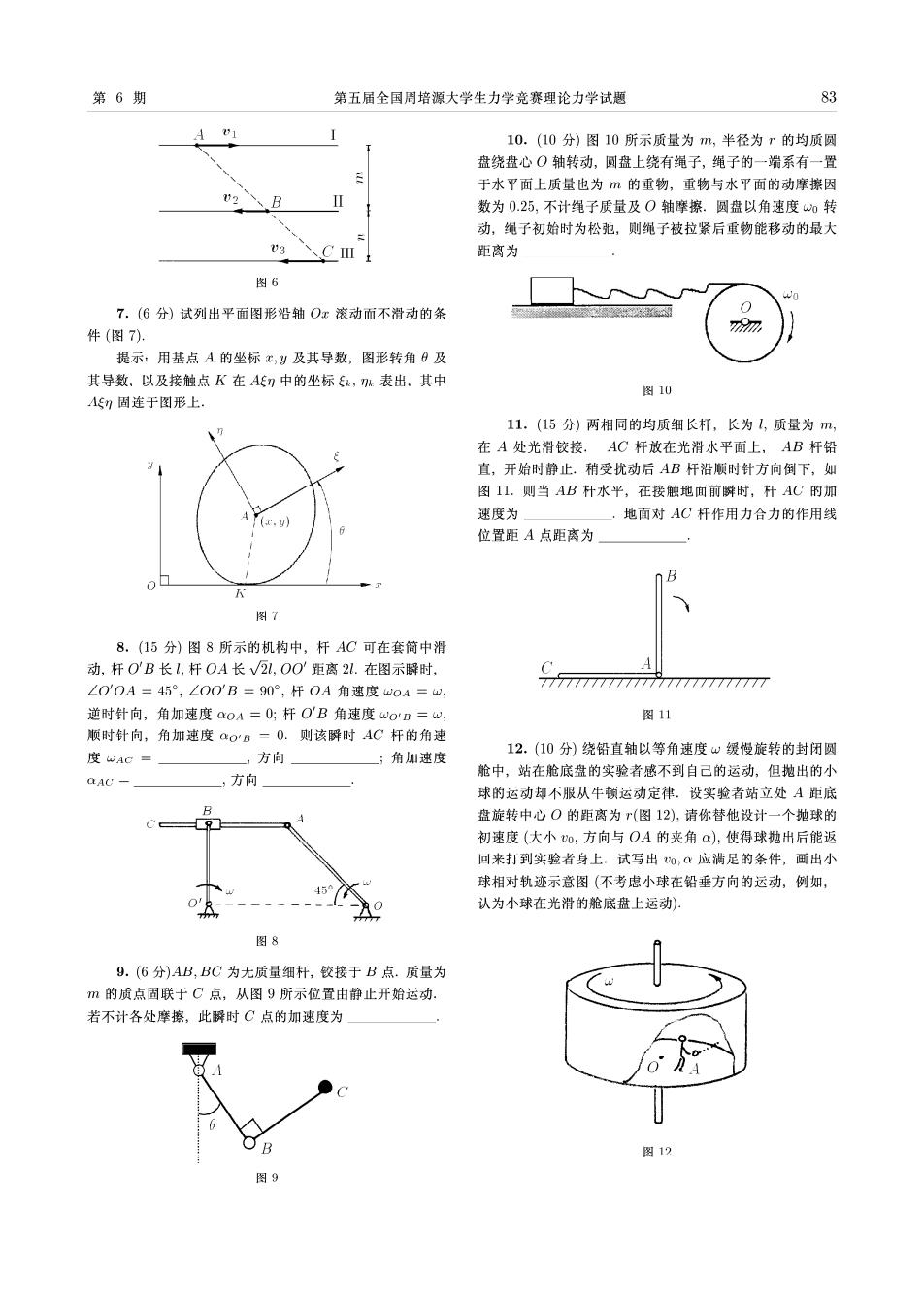
第6期 第五届全国周培源大学生力学竞赛理论力学试题 83 A 01 10.(10分)图10所示质量为m,半径为的均质圆 盘绕盘心O轴转动,圆盘上绕有绳子,绳子的一端系有一置 于水平面上质量也为的重物,重物与水平面的动摩擦因 "2 数为0.25,不计绳子质量及O轴摩擦.圆盘以角速度w0转 动,绳子初始时为松弛,则绳子被拉紧后重物能移动的最大 v3、CⅢ 距离为 图6 7.(6分)试列出平面图形沿轴Ox滚动而不滑动的条 件(图7). 77 提示,用基点A的坐标x,y及其导数,图形转角日及 其导数,以及接触点K在AE7中的坐标5x,k表出,其中 图10 4n固连于图形上. 11.(15分)两相同的均质细长打,长为1,质量为m, 在A处光滑铰接,AC杆放在光滑水平面上,AB杆铅 直,开始时静止,稍受扰动后AB杆沿顺时针方向倒下,如 图11.则当AB杆水平,在接触地面前瞬时,杆AC的加 速度为 ,地面对AC杆作用力合力的作用线 位置距A点距离为 n B 图7 8.(15分)图8所示的机构中,杆AC可在套筒中滑 动,杆OB长1,杆OA长√2l.OO'距离2l.在图示瞬时, ∠00A=45°,∠OOB=90°,杆OA角速度wO4=w, 777777777777777777777777777 逆时针向,角加速度aoA=0;杆O'B角速度o'D=w, 图11 顺时针向,角加速度ao'B-0.则该瞬时AC杆的角速 度wAC= ,方向 ;角加速度 12.(10分)绕铅直轴以等角速度w缓慢旋转的封闭圆 舱中,站在舱底盘的实验者感不到自己的运动,但抛出的小 方向 球的运动却不服从牛顿运动定律,设实验者站立处A距底 B 盘旋转中心O的距离为r(图12),请你替他设计一个抛球的 初速度(大小o,方向与OA的夹角a),使得球抛出后能返 回来打到实验者身上.试写出o,应满足的条件,画出小 球相对轨迹示意图(不考虑小球在铅垂方向的运动,例如, 认为小球在光滑的舱底盘上运动): 图8 9.(6分)AB,BC为尤质量细朴,铰接于B点.质量为 m的质点固联于C点,从图9所示位置由静止开始运动 若不计各处摩擦,此瞬时C点的加速度为 图12 图9

84 力学与实践 2004年第26卷 第五届全国周培源大学生力学竞赛材料力学试题 1.(10分)如图1所示,一根足够长的钢筋,放置在水 为EI,铰接于圆环内侧的直杆CD的拉压刚度为EA,承受 平刚性平台上.钢筋单位长度的重量为q,抗弯刚度为EI 均布切向载荷g和力偶矩Me作用,且Me=2rRq.试确 钢筋的一端伸出桌面边缘B的长度为α,试在下列两种情况 定杆CD的轴力与截面A的内力. 下计算钢筋自由端A的挠度fA. 5.(15分)图5所示放置在弹性基础上的细长杆,长为 (1)载荷F=0;(2)载荷F=qa. 1,两端铰支,承受轴向压力P.试建立临界载荷P,应满足 的方程.设基础反力的集度与梁挠度成正比并与挠度方向相 B 反,比例系数为,杆的抗弯刚度为EI 利性平台 P 杆 图1 777777 77777, 2.(10分)一变厚度薄壁圆管如图2所示,在两端承受 弹性基础 扭力偶矩M作用.已知管长为1,平均半径为R0,最小壁厚 为61,最大壁厚为2,壁厚6随(0≤6≤π)呈线性变化 图5 (上下对称),管材料的切变模量为G.试求方位角为日处的 6.(15分)图6所示均质等截面直梁AB,由高H处水 扭转切应力()与圆管两端相对转角p. 平白由坠落在刚性支座D⊥,梁仍处于弹性变形阶段.设梁 长为2,梁单位长重量为4,梁的抗弯刚度为EI.试求梁的 最大弯矩, B 图2 3.(15分)图3所示矩形藏面等直杆,常温时安装在支 座上.若杆底面与顶面温度分别升高T1与T2,且T。<T 并沿截面高度线性变化,试用能量法求横截面B的转角.设 图6 横截面的高度与宽度分别为h与b,材料的线膨胀系数为α. 7.(20分)图7所示传感器,AB和CD为铜片,其 厚度为宽度为b,长度为l,材料弹性模量为E.它们的自 由端与刚性杆BD刚性联接。 (1)试求截面F-F的轴力与弯矩; (2)如采用电测法测量截面F-F的轴力与弯矩,试确定 图3 贴片与接线方案(选择测量精度较高的方案),并建立由测试 应变计算相应内力的表达式 4.(15分)图4所示结构,已知小曲率圆环的弯曲刚度 6 图7 图4