
近代物理实验讲义 实验14阿贝成像与空间滤波 阿贝(E.Abb)首先提出显微镜成像原理以及随后的阿贝一波特空间滤波实验,在傅里叶 光学早期发展史上做出重要的贡献。这些实验简单、形象,令人信服,对相干光成像的机理及 频谱分析和综合原理做出深刻的解释,同时这种用简单的模板作滤波的方法一直延续至今,在 图像处理技术中仍然有广泛的应用价值。 【实验目的】 1、了解透镜的傅里叶变换性质,加深对空间频率、空间频谱和空间滤波等概念的理解: 2、熟悉阿贝成像原理,从信息量的角度理解透镜孔径对分辨率的影响: 3、完成一维空间滤波、二维空间滤波及高通空间滤波。 【实验原理】 1阿贝成像原理 1873年,德国人阿贝在研究显微镜设计方案时,提出了空间频率、空间频谱及二次衍射成像 的概念,并进行了相应的实验研究。他认为:在相干光照明下,显微镜的成像可分为两个步骤。 第一步是通过物的夫琅禾费衍射,在物镜后焦面上形成一个衍射图样,第二步是这些衍射图样发 出的子波相干涉,在像平面上相干迭加形成物的像,通过目镜可以观察到这个像。 ↑Y 平行光 图141阿贝成像原理示意图 图14.1是阿贝成像原理示意图,图中物G是正弦振幅透射光栅,成像的第一步是光梧的夫 琅禾费衍射。在G上取代表正弦光栖中的某些透光缝4、B、C,由正弦光橱透出的所有方向的光 中,经计算知,只有三个方向的平行光是彼此相长地相干,会聚于焦平面F上,形成1、6和月 1第二步,把这些衍射图样1、6和(看成是相干的子波源,这三列波在像平面H上相干迭加, 就得到正弦光楊的像。 按频谱分析理论,谱面上的每一点均具有以下四点明确的物理意义: (1)谱面上任一光点对应若物面上的一个空间频率成分。 (2)光点离谱面中心的距离,标志着物面上该频率成分的高低,离中心远的点代表物面上的高 频成分,反映物的细节部分。靠近中心的点,代表物面的低频成分,反映物的粗轮廓。中
近代物理实验讲义 96 实验 14 阿贝成像与空间滤波 阿贝(E. Abbe)首先ᨀ出显微镜成像原理以及随后的阿贝—波特空间滤波实验,在傅里叶 光学早期发展史上做出重要的贡献。这些实验简单、形象,令人信服,对相干光成像的机理及 频谱分析和综合原理做出深刻的解释,同时这种用简单的模板作滤波的方法一直延续至今,在 图像处理技术中仍然有广泛的应用价值。 【实验目的】 1、 了解透镜的傅里叶变换性质,加深对空间频率、空间频谱和空间滤波等概念的理解; 2、 熟悉阿贝成像原理,从信息量的角度理解透镜孔径对分辨率的影响; 3、 完成一维空间滤波、二维空间滤波及高通空间滤波。 【实验原理】 1 阿贝成像原理 1873 年,德国人阿贝在研究显微镜设计方案时,ᨀ出了空间频率、空间频谱及二次衍射成像 的概念,并进行了相应的实验研究。他认为:在相干光照明下,显微镜的成像可分为两个步骤。 第一步是通过物的夫琅禾费衍射,在物镜后焦面上形成一个衍射图样,第二步是这些衍射图样发 出的子波相干涉,在像平面上相干迭加形成物的像,通过目镜可以观察到这个像。 图 14.1 阿贝成像原理示意图 图 14.1 是阿贝成像原理示意图,图中物 G 是正弦振幅透射光栅,成像的第一步是光栅的夫 琅禾费衍射。在 G 上取代表正弦光栅中的某些透光缝 A、B、C,由正弦光栅透出的所有方向的光 中,经计算知,只有三个方向的平行光是彼此相长地相干,会聚于焦平面 F 上,形成 f+1、f0 和 f- 1。第二步,把这些衍射图样 f+1、f0 和 f-1 看成是相干的子波源,这三列波在像平面 H 上相干迭加, 就得到正弦光栅的像。 按频谱分析理论,谱面上的每一点均具有以下四点明确的物理意义: (1) 谱面上任一光点对应着物面上的一个空间频率成分。 (2) 光点离谱面中心的距离,标志着物面上该频率成分的高低,离中心远的点代表物面上的高 频成分,反映物的细节部分。靠近中心的点,代表物面的低频成分,反映物的粗轮廓。中

阿贝成像与空间滤波 心亮点是0级衍射即零频,反映在像面上呈现均匀背景 (3)光点的方向,指出物平面上该频率成分的方向,例如横向的谱点表示物面有纵向桶缝。 (4)光点的强弱则显示物面上该频率成分的幅度大小。 由以上定性分析可以看出,阿贝的二次成像理论的第一次衍射是透镜对物作空间傅里叶变换 它把物的各种空间频率和相应的振幅一一展现在它的焦平面上。一般情况下,物体透过率的分布 不是简单的空间周期函数,它们具有复杂的空间须谱,故透镜焦平面上的衍射图样也是极复杂的。 第二次衍射是指空间频谱的衍射波在像平面上的相干迭加。如果在第二次衍射中,物体的全部空 间频谱都参与相干迭加成像,则像面与物面完全相似。如果在展现物的空间频谱的透镜焦平面上 插入某种光学器件(称之为空间滤波器),使某些空间频率成分被滤掉或被改变,则像平面上的像 就会被改变,这就是空间滤波和光学信息处理的基本思想。 在实际光学成像系统中,像和物不可能完全一样。这是由于透镜的孔径是有限的,总有一些 衍射角比较大的高次光线(高频信息)不能进入物镜而被丢掉。所以像的信息总是比物的少些。 由于高频信息主要反映物的细节,因此,无论显微镜有多大的放大倍数,也不可能在像面上分辨 出这些细节。这是限制显微镜分辨本领的根本原因。当物镜孔径极其小时,有可能只有零级衍射 通过物镜,这时像面上有亮的均匀背景而无像分布。 1二维博里叶变换和空间频谱 在信息光学中常用傅里叶变换来表达和处理光的成像过程。 设在物屏XY平面上光场的复振幅分布为g:,),根据傅里叶变换特性,可以将这样一个空 间分布展开成一系列二维基元函数xp2Ux+∫,y川的线性叠加,即 gx-∫∫G(f,)expli2Ux+fHd, (14.1) 式中人为x、y方向的空间频率,即单位长度内振幅起伏的次数,G分表示原函数gx,) 中相应于空间颜率为么、方的基元函数的权重,亦即各种空间频率的成分占多大的比例,也称为 光场(optical field)gx,)的空间频谱。G(,月可由g(x,y)的傅里叶变换求得 G(ff)-ffg(x.y)exp[-i2(fx+fy)rdy (14.2) x,月与G(,分是一对傅里叶变换式,G(,分称为gx,y)的傅里叶的变换,gx,)是G队 )的逆变换,它们分别描述了光场的空间分布及光场的频率分布,这两种描述是等效的。 当gx,)是空间周期函数时,空间频率是不连续的。例如空间周期为的一维函数gx,即 97
阿贝成像与空间滤波 97 心亮点是 0 级衍射即零频,反映在像面上呈现均匀背景。 (3) 光点的方向,指出物平面上该频率成分的方向,例如横向的谱点表示物面有纵向栅缝。 (4) 光点的强弱则显示物面上该频率成分的幅度大小。 由以上定性分析可以看出,阿贝的二次成像理论的第一次衍射是透镜对物作空间傅里叶变换, 它把物的各种空间频率和相应的振幅一一展现在它的焦平面上。一般情况下,物体透过率的分布 不是简单的空间周期函数,它们具有复杂的空间频谱,故透镜焦平面上的衍射图样也是极复杂的。 第二次衍射是指空间频谱的衍射波在像平面上的相干迭加。如果在第二次衍射中,物体的全部空 间频谱都参与相干迭加成像,则像面与物面完全相似。如果在展现物的空间频谱的透镜焦平面上 插入某种光学器件(称之为空间滤波器),使某些空间频率成分被滤掉或被改变,则像平面上的像 就会被改变,这就是空间滤波和光学信息处理的基本思想。 在实际光学成像系统中,像和物不可能完全一样。这是由于透镜的孔径是有限的,总有一些 衍射角比较大的高次光线(高频信息)不能进入物镜而被丢掉。所以像的信息总是比物的少些。 由于高频信息主要反映物的细节,因此,无论显微镜有多大的放大倍数,也不可能在像面上分辨 出这些细节。这是限制显微镜分辨本领的根本原因。当物镜孔径极其小时,有可能只有零级衍射 通过物镜,这时像面上有亮的均匀背景而无像分布。 1 二维傅里叶变换和空间频谱 在信息光学中常用傅里叶变换来表达和处理光的成像过程。 设在物屏 X-Y 平面上光场的复振幅分布为 g(x, y),根据傅里叶变换特性,可以将这样一个空 间分布展开成一系列二维基元函数 exp[i2 ( f x f y)] π x + y 的线性叠加,即 ∫ ∫ +∞ −∞ = x y x + y x y g(x, y) G( f , f ) exp[i2π ( f x f y)]df df (14.1) 式中 fx、fy 为 x、y 方向的空间频率,即单位长度内振幅起伏的次数,G(fx, fy)表示原函数 g(x,y) 中相应于空间频率为 fx、fy 的基元函数的权重,亦即各种空间频率的成分占多大的比例,也称为 光场(optical field)g(x,y)的空间频谱。G(fx, fy)可由 g (x,y)的傅里叶变换求得 ∫∫ +∞ −∞ G f f = g x y −i f x + f y dxdy x y x y ( , ) ( , ) exp[ 2π( )] (14.2) g(x,y)与 G(fx, fy)是一对傅里叶变换式,G(fx, fy)称为 g(x,y)的傅里叶的变换,g(x,y)是 G(fx, fy)的逆变换,它们分别᧿述了光场的空间分布及光场的频率分布,这两种᧿述是等效的。 当 g(x,y)是空间周期函数时,空间频率是不连续的。例如空间周期为 x0 的一维函数 g(x),即

近代物理实验讲义 gxg(+x0.描述空间周期为的一维光栅时,光栅面上光振幅分布可展成傅里叶级数 g)-∑G.expr2寸x)-∑G.exp(2fo) (14.3) 上式中,n=0,±山,±2,:0-1,称为基频:-%,是基频的整数倍频,称为n次谐波的 频率。Gm是gx)的空间颜率,由傅里叶变换得 c-eR-2at. (14.4) 2透镜的二维傅里叶变换性质 在光学上,透镜是一个傅里叶变换器,它具有二维傅里叶变换的本领。理论证明,若在焦距 为F的正透镜L的前焦面(XY面)上放一光场振幅透过率为gx,)的物屏,并以波长为的相 干平行光照射,则在L的后焦面(XY面)上就得到gx,y)的傅里叶变换,即gx,y)的颜谱, 此即夫琅禾费衍射情况。其空间频谱 G元京了∫gep-2m元+示h (14.5) 其中空间频率人人与透镜像方焦面(频谱面)上的坐标有如下关系 f-x'IAF fy-y'/AF (14.6) 里叶变换,这就为函数的傅里叶变换提供了一种光学手段,将抽象的函数演算变成了实实在在的 物理过程。由于亦示分别正比于少所以当入。F一定时,频谱面上远商坐标原点的点对 应于物频谱中的高频部分,中心点x与y0,=0对应于零频。 4空间滤波和光信息处理 光信息处理是通过空间滤波器来实现的,所谓空间滤波器是指在图14.1中透镜的后焦平面上 放置某种光学元件来改造或选取所需要的信息,以实现光信总处理。这种光学器件称为空间滤波 器。 图142给出了几种常用的空间滤波器。 ()低通滤波:目的是滤去高频成分,保留低频成分。由于低频成分集中在谱面的光轴(中心)附 近,高频成分落在远离中心的地方,经低通滤波后图像的精细结构将消失,黑白突变处也变得模 糊。 (b)高通滤波:目的是滤去低频成分而让高频成分通过,其结果正好与低通滤波相反,使物的细节
近代物理实验讲义 98 g(x)=g (x+x0)。᧿述空间周期为 x0 的一维光栅时,光栅面上光振幅分布可展成傅里叶级数 ( ) = ∑ exp( 2 ) = ∑ exp( 2 ) 0 g x G i f x G i nf x n π n n π (14.3) 上式中,n=0,±1,±2,……;f0=1/x0 ,称为基频;fn=nf0,是基频的整数倍频,称为 n 次谐波的 频率。Gn 是 g(x)的空间频率,由傅里叶变换得 g x i nf x dx x G x x n ( ) exp( 2 ) 1 0 / 2 0 / 2 0 0 = − π ∫ + − (14.4) 2 透镜的二维傅里叶变换性质 在光学上,透镜是一个傅里叶变换器,它具有二维傅里叶变换的本领。理论证明,若在焦距 为 F 的正透镜 L 的前焦面(X-Y 面)上放一光场振幅透过率为 g(x,y)的物屏,并以波长为λ的相 干平行光照射,则在 L 的后焦面(Xʹ-Yʹ面)上就得到 g(x,y)的傅里叶变换,即 g(x,y)的频谱, 此即夫琅禾费衍射情况。其空间频谱 ∫ ∫ +∞ −∞ ʹ + ʹ = − ʹ ʹ y dxdy F y x F x g x y i F y F x G( , ) ( , ) exp[ 2 ( )] λ λ π λ λ (14.5) 其中空间频率 fx、fy 与透镜像方焦面(频谱面)上的坐标有如下关系 f x = xʹ/ λF f y = yʹ/ λF (14.6) 显然, ( , ) F y F x G λ λ ʹ ʹ 就是空间频率为( F y F x λ λ ʹ ʹ , )的频谱项的复振幅,是物的复振幅分布的傅 里叶变换,这就为函数的傅里叶变换ᨀ供了一种光学手段,将抽象的函数演算变成了实实在在的 物理过程。由于 F y F x λ λ ʹ ʹ , 分别正比于 xʹ,yʹ,所以当λ、F 一定时,频谱面上远离坐标原点的点对 应于物频谱中的高频部分,中心点 xʹ=yʹ=0,fx=fy=0 对应于零频。 4 空间滤波和光信息处理 光信息处理是通过空间滤波器来实现的,所谓空间滤波器是指在图 14.1 中透镜的后焦平面上 放置某种光学元件来改造或选取所需要的信息,以实现光信息处理。这种光学器件称为空间滤波 器。 图 14.2 给出了几种常用的空间滤波器。 (a)低通滤波:目的是滤去高频成分,保留低频成分。由于低频成分集中在谱面的光轴(中心)附 近,高频成分落在远离中心的地方,经低通滤波后图像的精细结构将消失,黑白突变处也变得模 糊。 (b)高通滤波:目的是滤去低频成分而让高频成分通过,其结果正好与低通滤波相反,使物的细节

阿贝成像与空间滤波 及边缘清晰。 (心)带通滤波:根据需要,有选择的滤掉某些频率成分。 (方向滤波:只让某一方向,例如纵向的频率成分通过,则像面上将突出了物的横向线条。 O 〔a)低通 (b)高通 (c)带通 (b)方向 图142空间滤波器示意图 假如用一块二维矩形光栅作为物,二维矩形光栅的空间结构分布如图14.3(,则在频谱面上 将显示出二维光栅的频谱,如图14.3b)所示。假如用一块有狭缝的屏作空间滤波器,将狭缝水平 放置在F面上,则透过的频率面如图14.3c)所示,此时在像平面上的像将如图14.3()所示。若将 狭缝垂直放置,则透过的频率面如图14.3(e)所示,像平面上的像将如图1430所示。如果让狭缝 45°倾斜,那么透镜的焦平面F上保留的频谱和像平面H上成的像将如图14.3g、h)所示。这表 明用一条狭缝作滤波器,当其取向不同时,可将二维光悟的物处理成上述各种方位的一维光栅的 像。 (a) (c) (e) a (f 图143空间滤波器及空间滤波效果示意图 以上是采用滤波器进行光信息处理的最简单的实例,这类滤波器从物体的全部空间信息中选 出所需要的部分,从而实现对物体信息的处理,获得由物体的部分空间信息所构成的像。 【实验步暖及靴据处理】 1、用激光器、L1、L2组成扩束系统,将激光束直径扩大,并测量其放大倍数。 2、用扩束后的平行光照射一维光栅,并用L3将其成像至2米外的白屏上。 3、将白屏放在L3的后焦面(傅氏面)上,可以观察到水平排列的一些清晰光点。这些光点相应 于光栅的0,±1,±2.,级衍射极大值,用米尺大约测出各光点与中央最亮点的距离x,试 求出这些光点的空间频率 4、在L3后焦面(付氏面)处放入频谱滤波器(可调独缝),档去0级以外的各点,观察像面(2
阿贝成像与空间滤波 99 及边缘清晰。 (c)带通滤波:根据需要,有选择的滤掉某些频率成分。 (d)方向滤波:只让某一方向,例如纵向的频率成分通过,则像面上将突出了物的横向线条。 图 14.2 空间滤波器示意图 假如用一块二维矩形光栅作为物,二维矩形光栅的空间结构分布如图 14.3(a),则在频谱面上 将显示出二维光栅的频谱,如图 14.3(b)所示。假如用一块有狭缝的屏作空间滤波器,将狭缝水平 放置在 F 面上,则透过的频率面如图 14.3(c)所示,此时在像平面上的像将如图 14.3(d)所示。若将 狭缝垂直放置,则透过的频率面如图 14.3(e)所示,像平面上的像将如图 14.3(f)所示。如果让狭缝 45°倾斜,那么透镜的焦平面 F 上保留的频谱和像平面 H 上成的像将如图 14.3(g、h)所示。这表 明用一条狭缝作滤波器,当其取向不同时,可将二维光栅的物处理成上述各种方位的一维光栅的 像。 图 14.3 空间滤波器及空间滤波效果示意图 以上是采用滤波器进行光信息处理的最简单的实例,这类滤波器从物体的全部空间信息中选 出所需要的部分,从而实现对物体信息的处理,获得由物体的部分空间信息所构成的像。 【实验步骤及数据处理】 1、 用激光器、L1、L2 组成扩束系统,将激光束直径扩大,并测量其放大倍数。 2、 用扩束后的平行光照射一维光栅,并用 L3 将其成像至 2 米外的白屏上。 3、 将白屏放在 L3 的后焦面(傅氏面)上,可以观察到水平排列的一些清晰光点。这些光点相应 于光栅的 012 , , ...... ± ± 级衍射极大值,用米尺大约测出各光点与中央最亮点的距离 ' x ,试 求出这些光点的空间频率。 4、 在 L3 后焦面(付氏面)处放入频谱滤波器(可调狭缝),档去 0 级以外的各点,观察像面(2
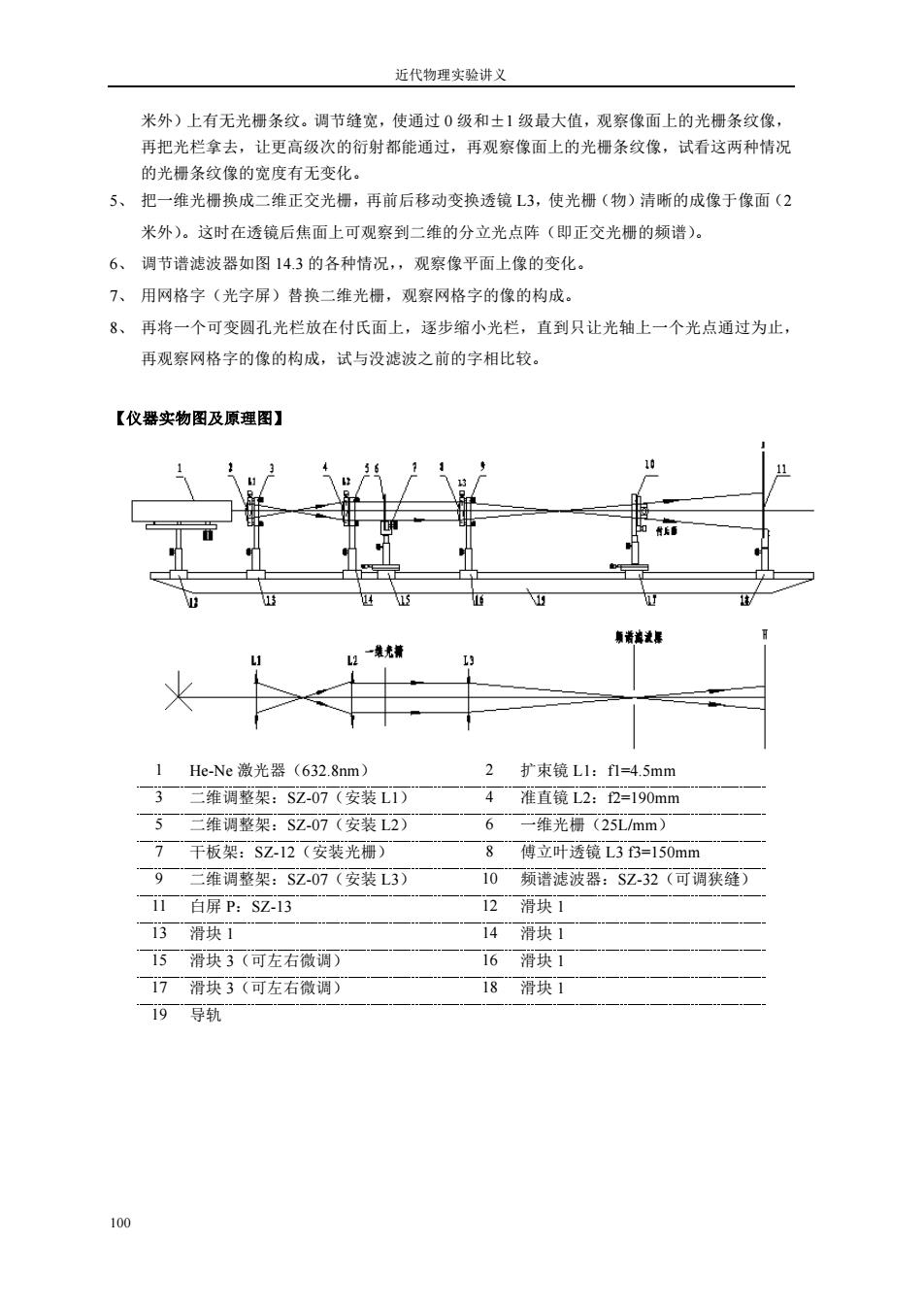
近代物理实验讲义 米外)上有无光栅条纹。调节缝宽,使通过0级和士1级最大值,观察像面上的光栅条纹像, 再把光栏拿去,让更高级次的衍射都能通过,再观察像面上的光栅条纹像,试看这两种情况 的光栅条纹像的宽度有无变化 5、 把一维光栅换成二维正交光栅,再前后移动变换透镜L3,使光栅(物)清晰的成像于像面(2 米外)。这时在透镜后焦面上可观察到二维的分立光点阵(即正交光栅的频谱)。 6、调节谱滤波器如图14.3的各种情况,观察像平面上像的变化。 7、用网格字(光字屏)替换二维光栅,观察网格字的像的构成。 8、再将一个可变圆孔光栏放在付氏面上,逐步缩小光栏,直到只让光轴上一个光点通过为止 再观察网格字的像的构成,试与没滤波之前的字相比较。 【仪器实物图及原理图】 He-Ne激光器(632.8nm) 2扩束镜Ll:f1=4.5mm 3 二维调整架:SZ-07(安装L1) 4准直镜L2:f2=190mm 5二维调整塑:S707(安装12) 6一维光栅(25Lmm) 干板架:SZ-12(安装光栅) 8傅立叶透镜L33=150mm 9一维调整架:SZ-07(安装13) 10频谱滤波器:SZ32(可调张缝) 1白屏P:sZ.13 12滑块1 13滑块1 14滑块1 5滑块3(可左右微调 16滑块1 17滑块3(可左右微调) 18滑块1 一19导轨 100
近代物理实验讲义 100 米外)上有无光栅条纹。调节缝宽,使通过 0 级和±1 级最大值,观察像面上的光栅条纹像, 再把光栏拿去,让更高级次的衍射都能通过,再观察像面上的光栅条纹像,试看这两种情况 的光栅条纹像的宽度有无变化。 5、 把一维光栅换成二维正交光栅,再前后移动变换透镜 L3,使光栅(物)清晰的成像于像面(2 米外)。这时在透镜后焦面上可观察到二维的分立光点阵(即正交光栅的频谱)。 6、 调节谱滤波器如图 14.3 的各种情况,,观察像平面上像的变化。 7、 用网格字(光字屏)替换二维光栅,观察网格字的像的构成。 8、 再将一个可变圆孔光栏放在付氏面上,逐步缩小光栏,直到只让光轴上一个光点通过为止, 再观察网格字的像的构成,试与没滤波之前的字相比较。 【仪器实物图及原理图】 1 He-Ne 激光器(632.8nm) 2 扩束镜 L1:f1=4.5mm 3 二维调整架:SZ-07(安装 L1) 4 准直镜 L2:f2=190mm 5 二维调整架:SZ-07(安装 L2) 6 一维光栅(25L/mm) 7 干板架:SZ-12(安装光栅) 8 傅立叶透镜 L3 f3=150mm 9 二维调整架:SZ-07(安装 L3) 10 频谱滤波器:SZ-32(可调狭缝) 11 白屏 P:SZ-13 12 滑块 1 13 滑块 1 14 滑块 1 15 滑块 3(可左右微调) 16 滑块 1 17 滑块 3(可左右微调) 18 滑块 1 19 导轨