
电磁场与电磁波基础 主讲:徐乐 商要子作找以是国
电磁场与电磁波基础 主讲:徐乐

Review ·矢量分析导论 一矢性函数 一矢性函数的导数与微分 一矢性函数的积分 ·场论导论 一场论初窥 -数量场的梯度 一矢量场的矢量线 lexu@mail.xidian.edu.cn 2
Review • 矢量分析导论 – 矢性函数 – 矢性函数的导数与微分 – 矢性函数的积分 • 场论导论 – 场论初窥 – 数量场的梯度 – 矢量场的矢量线 lexu@mail.xidian.edu.cn 2
Review 数量场 0吧 0 等值面 梯度 矢量场 00 宏观分析 微观分析 lexu@mail.xidian.edu.cn 3
Review 3 数量场 等值面 梯度 矢量场 宏观分析 微观分析 lexu@mail.xidian.edu.cn
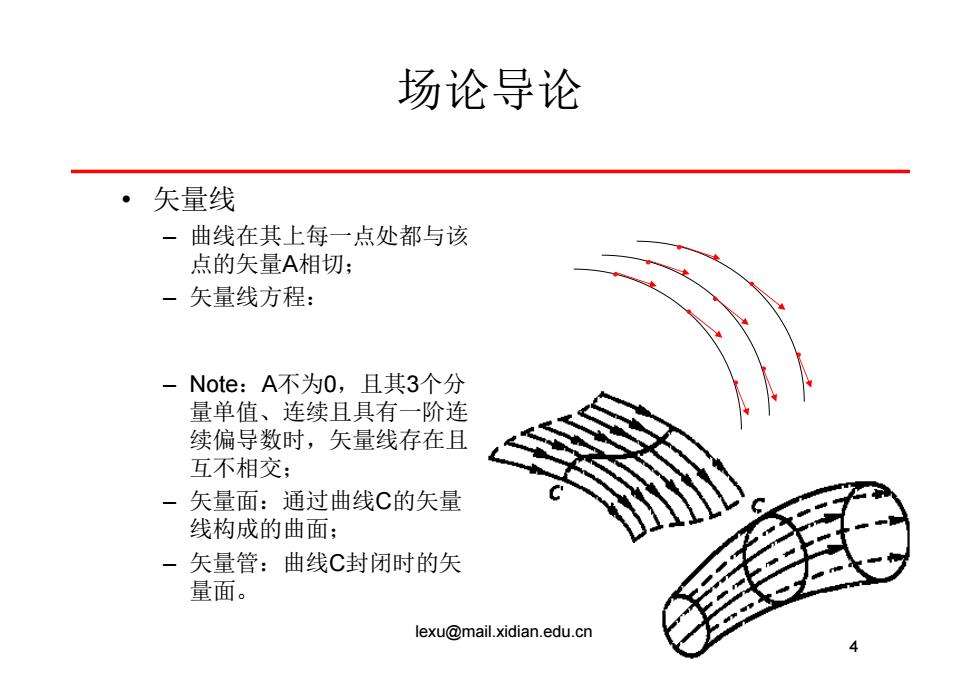
场论导论 ·矢量线 - 曲线在其上每一点处都与该 点的矢量A相切; 一矢量线方程: -Note:A不为0,且其3个分 量单值、连续且具有一阶连 续偏导数时,矢量线存在且 互不相交; 一矢量面:通过曲线C的矢量 线构成的曲面; 矢量管:曲线C封闭时的矢 量面。 lexu@mail.xidian.edu.cn
场论导论 • 矢量线 – 曲线在其上每一点处都与该 点的矢量A相切; – 矢量线方程: – Note:A不为0,且其3个分 量单值、连续且具有一阶连 续偏导数时,矢量线存在且 互不相交; – 矢量面:通过曲线C的矢量 线构成的曲面; – 矢量管:曲线C封闭时的矢 量面。 4 lexu@mail.xidian.edu.cn
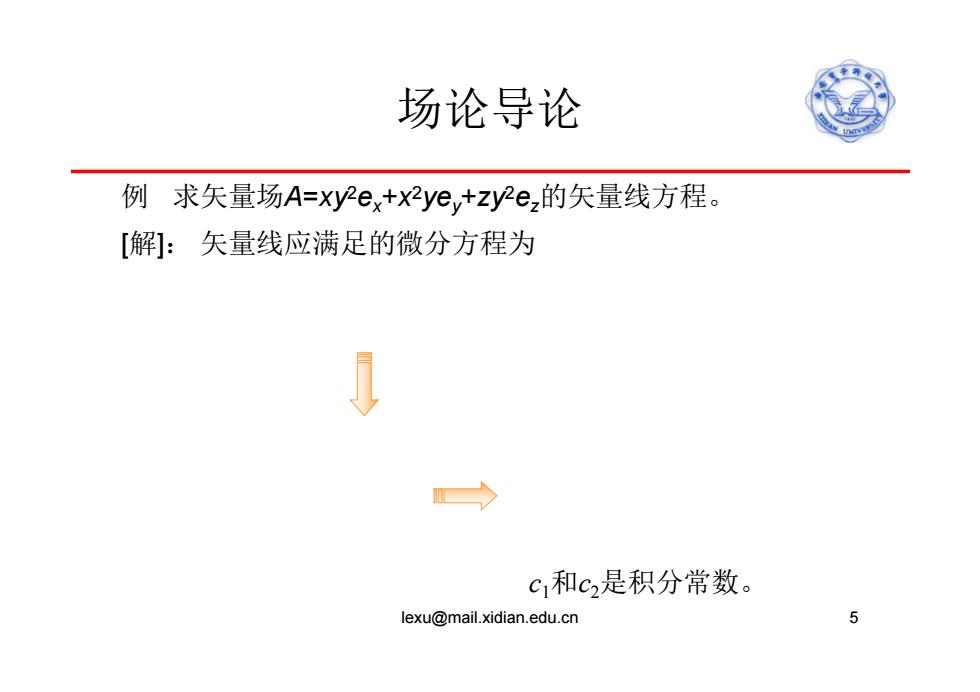
场论导论 例求矢量场A=y2ex+x2yev+zy2ez的矢量线方程。 [解]:矢量线应满足的微分方程为 c1和c2是积分常数。 lexu@mail.xidian.edu.cn 5
场论导论 例 求矢量场A=xy2ex+x2yey+zy2ez的矢量线方程。 [解]: 矢量线应满足的微分方程为 5 c1和c2是积分常数。 lexu@mail.xidian.edu.cn

场论导论 ·两条曲线 矢端曲线 矢量线 lexu@mail.xidian.edu.cn 6
场论导论 • 两条曲线 6 矢端曲线 矢量线 lexu@mail.xidian.edu.cn

第2讲矢量场分析 。 矢量场的通量与散度 一矢量场的通量 一矢量场的散度 ·矢量场的环量与旋度 一矢量场的环量 一矢量场的旋度 ·曲线坐标系 亥姆霍兹定理 lexu@mail.xidian.edu.cn
第2讲 矢量场分析 • 矢量场的通量与散度 – 矢量场的通量 – 矢量场的散度 • 矢量场的环量与旋度 – 矢量场的环量 – 矢量场的旋度 • 曲线坐标系 • 亥姆霍兹定理 lexu@mail.xidian.edu.cn 7
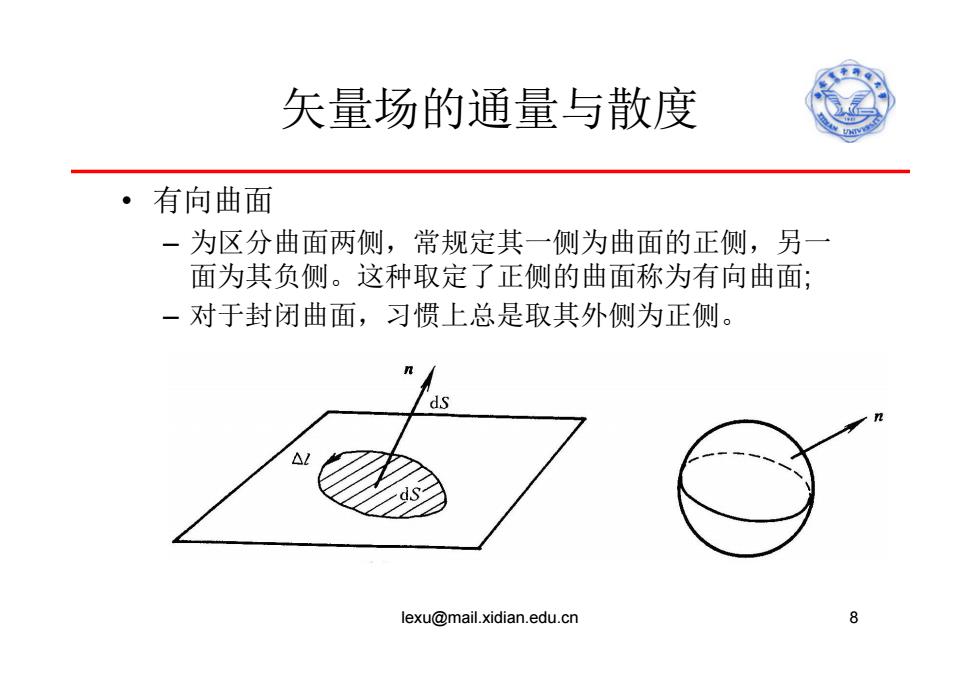
矢量场的通量与散度 ·有向曲面 一为区分曲面两侧,常规定其一侧为曲面的正侧,另一 面为其负侧。这种取定了正侧的曲面称为有向曲面; 一对于封闭曲面,习惯上总是取其外侧为正侧。 ds lexu@mail.xidian.edu.cn 8
矢量场的通量与散度 • 有向曲面 – 为区分曲面两侧,常规定其一侧为曲面的正侧,另一 面为其负侧。这种取定了正侧的曲面称为有向曲面; – 对于封闭曲面,习惯上总是取其外侧为正侧。 lexu@mail.xidian.edu.cn 8

矢量场的通量与散度 ·流量 -设s为流速场(M中一有向曲面,考虑单位时间流体向 正侧穿过s的流量Q。(正向指向s正侧) -在s上取ds,ds足够小以至于ds上各点处曲面法向及流 体流矢均与M处和相同。流体穿过ds的流量为: 一单位时间内沿正向穿过$的总流量为 ·数学上把这种形式的曲面积分称为通量。 lexu@mail.xidian.edu.cn 9
S M 矢量场的通量与散度 • 流量 – 设s为流速场v(M)中一有向曲面,考虑单位时间流体向 正侧穿过s的流量Q。(正向指向s正侧) – 在s上取ds,ds足够小以至于ds上各点处曲面法向及流 体流矢均与M处和相同。流体穿过ds的流量为: – 单位时间内沿正向穿过s的总流量为 • 数学上把这种形式的曲面积分称为通量。 lexu@mail.xidian.edu.cn 9

矢量场的通量与散度 ·通量 -将曲面S各面元上的A·dS相加,它表示矢量场A穿过整 个曲面S的通量,也称为矢量A在曲面S上的面积分 - 设A(M0为一矢量场,沿其中有向曲面s正(负)侧曲面积 分称为矢量场A(M)向s正(负)侧穿过曲面s的通量。 ·如果曲面是一个开曲面,则 ·如果曲面是一个闭曲面,则 lexu@mail.xidian.edu.cn 10
矢量场的通量与散度 • 通量 – 将曲面 S各面元上的A·dS相加,它表示矢量场 A穿过整 个曲面 S的通量,也称为矢量 A在曲面 S上的面积分 – 设 A ( M )为一矢量场,沿其中有向曲面 s 正 ( 负 )侧曲面积 分称为矢量场 A ( M ) 向 s 正 ( 负 )侧穿过曲面 s 的通量 。 • 如果曲面是一个开曲面,则 • 如果曲面是一个闭曲面,则 lexu@mail.xidian.edu.cn 10