
Review ·电偶极子 ·介质极化 D=80E+P ·束缚电荷 Psp=P.i.Pp=-V.P ·介质高斯定理 ∮Ds=0 (D2-D)=p 091-62 On 02=Ps ·介质中的场方程 ∮Edl=0 ● 静电场边界条件 D=8E n×E1=n×E2p2-p=0 2011年6月10日星期五 lexu@mail.xidian.edu.cn 2
2011年6月10日星期五 lexu@mail.xidian.edu.cn 2 Review 电偶极子 介质极化 束缚电荷 介质高斯定理 介质中的场方程 静电场边界条件 ( ) 0 0 1 1 4 4 S V P n P dS dV r r r r φ πε πε −∇ ⋅′ ⋅ = ′ ′ + − − ′ ′ ∫ ∫ PED ε 0 += 0 S l D dS Q E dl D Eε ⋅ = ⋅ = = ∫ ∫ 1 EnEn 2 ×=× 2 1 ( ) s nD D ⋅−= ρ S nn ρ ϕ ε ϕ ε = ∂ ∂ − ∂ ∂ 2 2 1 1 0 ϕϕ 12 =− , ρ ρ S p = ⋅ = −∇ ⋅ Pn P p XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

静电场中的导体系统 。当电场中存在导体时,在外电场的作用下导体内部的电子做宏观 运动,其结果是: 。一方面影响导体外的电场分布; 。另一方面使导体内部的总电场为零。 ●物理解释 。重新分布的电荷会在导体内产生相应的电场,而该电场与外电场 的方向相反,当电荷的宏观运动达到平衡时(即分布达到稳定状 态),分布电荷的电场恰与外部电场相互抵消。 。平衡状态时的导体成为等位体,表面成为等位面 2011年6月10日星期五 lexu@mail.xidian.edu.cn
2011年6月10日星期五 lexu@mail.xidian.edu.cn 3 静电场中的导体系统 当电场中存在导体时,在外电场的作用下导体内部的电子做宏观 运动,其结果是: 一方面影响导体外的电场分布; 另一方面使导体内部的总电场为零。 物理解释 重新分布的电荷会在导体内产生相应的电场,而该电场与外电场 的方向相反,当电荷的宏观运动达到平衡时(即分布达到稳定状 态),分布电荷的电场恰与外部电场相互抵消。 平衡状态时的导体成为等位体,表面成为等位面 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

导体系统的电容 ·静电平衡时,导体内部电场为零,导体本身是等位体: ●导体表面是等位面,内部无电荷,电荷分布在导体表面; ●在多导体系统中,每个导体携带电荷一定,它们的电位及其电荷 面密度完全由各导体几何形状、相对位置和导体间介质特性等系 统结构参数决定; ·为描述这种关系,引入电位系数、电容系数及部分电容的概念。 2011年6月10日星期五 lexu@mail.xidian.edu.cn
2011年6月10日星期五 lexu@mail.xidian.edu.cn 4 导体系统的电容 静电平衡时,导体内部电场为零,导体本身是等位体; 导体表面是等位面,内部无电荷,电荷分布在导体表面; 在多导体系统中,每个导体携带电荷一定,它们的电位及其电荷 面密度完全由各导体几何形状、相对位置和导体间介质特性等系 统结构参数决定; 为描述这种关系,引入电位系数、电容系数及部分电容的概念。 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

导体系统的电容 ·带有等值异号电荷的两个导体构成一个电容器 电容是描述这两个导体系统物理属性的一个物理量 。其大小与导体的形状、尺寸、相对位置以及导体周围的介质 有关。 。电容与两导体所带电荷及其间电位差有如下关系: C= 电容与导体的带电情况无关:《U=Ed,而E与9成正比) ● ·一个孤立的导体可认为是它与无穷远处的导体构成的一个特殊的 电容器 2011年6月10日星期五 lexu@mail.xidian.edu.cn
2011年6月10日星期五 lexu@mail.xidian.edu.cn 5 导体系统的电容 带有等值异号电荷的两个导体构成一个电容器 电容是描述这两个导体系统物理属性的一个物理量 其大小与导体的形状、尺寸、相对位置以及导体周围的介质 有关。 电容与两导体所带电荷及其间电位差有如下关系: 电容与导体的带电情况无关。( ,而E与q成正比) 一个孤立的导体可认为是它与无穷远处的导体构成的一个特殊的 电容器 U q C = ∫ ⋅= 2 1 导体 导体 ldEU XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

导体系统的电容 ·电容的求法通常遵循以下步骤: 。1.假设两导体上所带电荷q,并根据实际情况求出电荷分布。 。2.由电荷分布求出电场强度,从而得出两导体电位差 U-=∫Edi 。3.由电容定义求出电容。 2011年6月10日星期五 lexu@mail.xidian.edu.cn
2011年6月10日星期五 lexu@mail.xidian.edu.cn 6 导体系统的电容 电容的求法通常遵循以下步骤: 1. 假设两导体上所带电荷q,并根据实际情况求出电荷分布。 2. 由电荷分布求出电场强度,从而得出两导体电位差 3. 由电容定义求出电容。 ∫ ⋅= 2 1 ldEU XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

导体系统的电容 例平行双导线单位长电容(d<<D) 0 。[解]因为d<<D ,导线上的电荷分布可看作是密度为P,的线 电荷,由高斯定理可知: P 2π6o' 瓦,=,Aa 2π8o2 2011年6月10日星期五 lexu@mail.xidian.edu.cn
2011年6月10日星期五 lexu@mail.xidian.edu.cn 7 导体系统的电容 例 平行双导线单位长电容( ) [解]因为 ,导线上的电荷分布可看作是密度为ρl 的线 电荷,由高斯定理可知: << Dd << Dd 1 1 0 1 2 2 0 2 2 2 l r l r E a r E a r ρ π ε ρ π ε = − = XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

导体系统的电容 在x轴上 2a.2D-可 、2元8X P 两导饰同电为:0-后a-2会 P 2m(D-对 d D-d 2[nx-n(D-x刘]2a 2π80 2πE0 D-xd =eInD-d TE0 单位长度电容: C=PL=- π6 U D-d d 2011年6月10日星期五 lexu@mail.xidian.edu.cn 8
2011年6月10日星期五 lexu@mail.xidian.edu.cn 8 导体系统的电容 在x轴上 两导体间电压为: 单位长度电容: ( ) 1 2 0 0 , 2 2 l l E aE x x a x D x ρ ρ πε πε = = − ( ) ( ) 0 0 0 0 0 2 2 ln ln ln 2 2 ln D d l l d D d D d l l d d l U E dl dx x Dx x x Dx D x D d d ρ ρ πε πε ρ ρ π ε πε ρ πε − − − = ⋅= + − = −− = − − = ∫ ∫ d U dD C l − == ln ρ πε 0 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
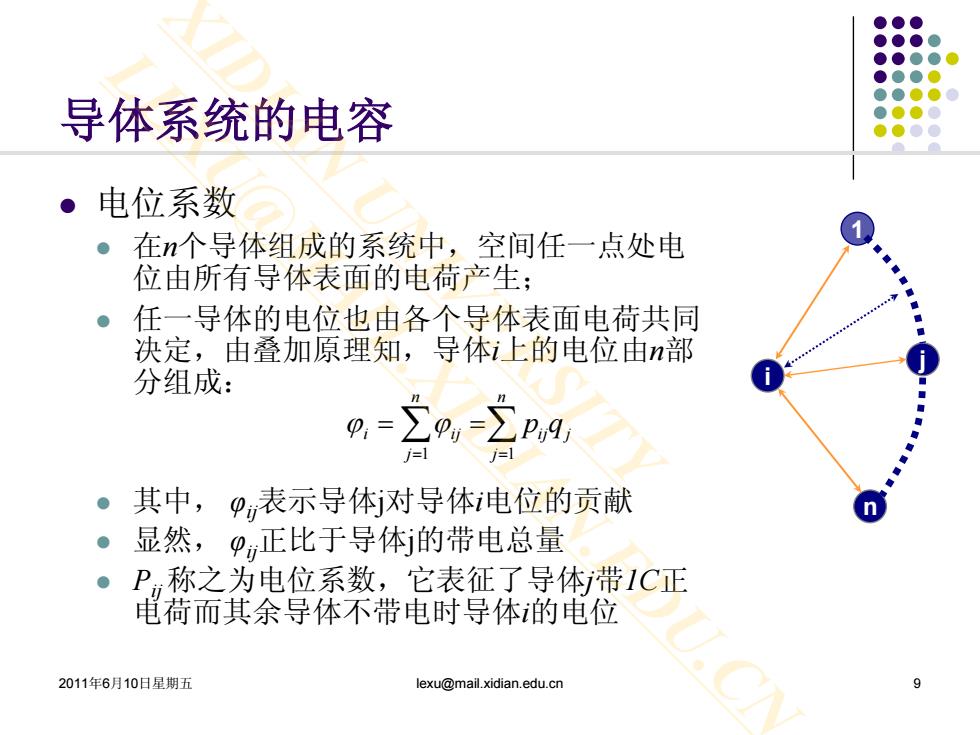
导体系统的电容 电位系数 。在n个导体组成的系统中,空间任一点处电 位由所有导体表面的电荷产生; 任一导体的电位也由各个导体表面电荷共同 决定,由叠加原理知,导体i上的电位由n部 分组成: i=l 其中,9,表示导体j对导体电位的贡献 n 。显然,正比于导体j的带电总量 P称之为电位系数,它表征了导体带1C正 电荷而其余导体不带电时导体的电位 2011年6月10日星期五 lexu@mail.xidian.edu.cn
2011年6月10日星期五 lexu@mail.xidian.edu.cn 9 导体系统的电容 电位系数 在n个导体组成的系统中,空间任一点处电 位由所有导体表面的电荷产生; 任一导体的电位也由各个导体表面电荷共同 决定,由叠加原理知,导体i上的电位由n部 分组成: 其中, φij表示导体j对导体i电位的贡献 显然, φij正比于导体j的带电总量 Pij 称之为电位系数,它表征了导体j带1C正 电荷而其余导体不带电时导体i的电位 ∑∑= = == n j ij j n j i ij qp 1 1 ϕϕ i n j 1 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

导体系统的电容 9=∑0,=2P,9 ·将该式通过线性方程组表示出来: p1=P1191+P1292++P1n9m p2=P2191+P2292+…+P2n9m 0n=Pn191+Pn292+…+Pm9m ●亦可写成矩阵形式 91 Pu P12 91 [o]=[p][q Pz P21 P22 P2n 92 2011年6月10日星期五 ana Pn2 10
2011年6月10日星期五 lexu@mail.xidian.edu.cn 10 导体系统的电容 将该式通过线性方程组表示出来: 亦可写成矩阵形式 ∑∑= = == n j ij j n j i ij qp 1 1 ϕϕ 1 11 1 12 2 1 2 21 1 22 2 2 11 2 2 n n n n n n n nn n pq pq pq pq pq pq pq pq pq ϕ ϕ ϕ = + ++ = + ++ = + ++ 1 11 12 1 1 2 21 22 2 2 1 2 n n n n n nn n pp pq pp pq pp pq ϕ ϕ ϕ = ϕ = [][ ][qp ] XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

导体系统的电容 以P为例,由电位系数的定义可知: 。导体带正电,电力线自导体出发,终 止于导体上或终止于地面上。 。导体不带电,有多少电力线终止于它, 就有多少电力线自它发出,所发出的电 力线不是终止于其它导体上,就是终止 于地面。 n ● 电位沿电力线下降,其它导体电位必介 于导体的电位和地面电位之间 Ground Pi>P,≥0 电位系数在互易介质中 Pu Pi [e]=[s]T 2011年6月10日星期五 lexu@mail.xidian.edu.cn [四=[]P
2011年6月10日星期五 lexu@mail.xidian.edu.cn 11 导体系统的电容 以Pij为例,由电位系数的定义可知: 导体j带正电,电力线自导体j出发,终 止于导体i上或终止于地面上。 导体i不带电,有多少电力线终止于它, 就有多少电力线自它发出,所发出的电 力线不是终止于其它导体上,就是终止 于地面。 电位沿电力线下降,其它导体电位必介 于导体j的电位和地面电位之间 电位系数在互易介质中 i n j 1 Ground pp ijjj ≥> 0 jiij = pp T T [] [] [] [] ε ε µ µ = = XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN