
Review 边值问题的分类 。唯一性定理 ● 镜象原理 NIVERSITY IL.XIDIAN.EDU.C 2
2 Review 边值问题的分类 唯一性定理 镜象原理 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
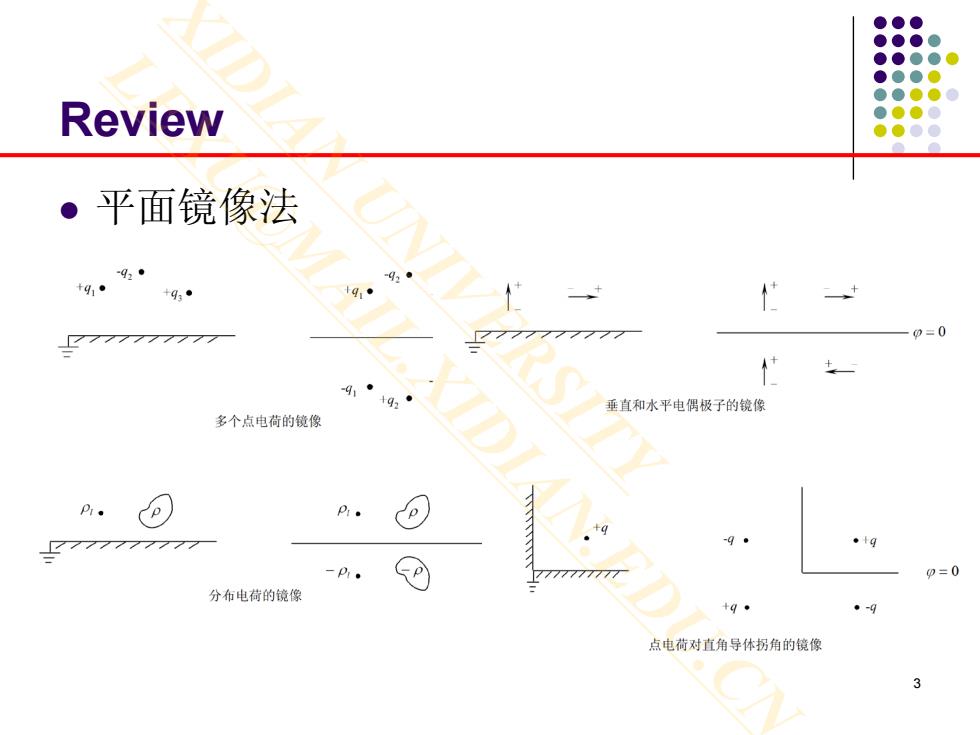
Review ·平面镜像法 g。· 93。 +93· 91● p=0 91。 垂直和水平电偶极子的镜像 多个点电荷的镜像 p 777777777 p=0 分布电荷的镜像 +9。 。-q 点电荷对直角导体拐角的镜像
3 Review 平面镜像法 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

第11讲静态场的解(川) ●●● ·球面镜像法 ●柱面镜像法 ·介质平面镜像法 。其它方法简介 NIVERSITY XIDIAN.EDU.C
4 第11讲 静态场的解(II) 球面镜像法 柱面镜像法 介质平面镜像法 其它方法简介 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

球面镜像法 。[模型]半径为a的接地导体球,点电荷位于距球心d处, 求球外任一点的电位。 ·[分析] 。球外仅有点电荷q,距球心距离d 。球面是等位面,半径a,接地,电位为零
5 球面镜像法 [模型I] 半径为a的接地导体球,点电荷位于距球心d处, 求球外任一点的电位。 [分析] 球外仅有点电荷q,距球心距离d 球面是等位面,半径a,接地,电位为零 a d q XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

球面镜像法 ·[模型]半径为a的球形边界面,点电荷q位于距球心d处,球 内距球心b处置以点电荷q',求球外任一点的电位。 ·[分析] ●球外仅有点电荷q,距球心距离d ●空间任一点电位由点电荷q和点电荷q共同决定 「1 0= 4π61 4π6'2 。球面电位为零 q q 十 =0 4π6'10 4π6'20
6 球面镜像法 [模型I] 半径为a的球形边界面,点电荷q位于距球心d处,球 内距球心b处置以点电荷q’,求球外任一点的电位。 [分析] 球外仅有点电荷q,距球心距离d 空间任一点电位由点电荷q和点电荷q’共同决定 球面电位为零 d q q’ b r1 r2 r 10 4 20 ' 4 r q r q πεπε ϕ += 0 4 ' 4 0 10 0 20 =+ r q r q πεπε XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

球面镜像法 —=0 4π610 4π6'20 ·1o、2o是从q、q到球面上点的距离 110 ·q和b待定 ·取球面上的点分别位于A、B两点,可以得到确定g、b的两个方程: 9+9=0 a 9=- 4= =-9 d-a a-b 1r20 ld-al rio 9+9八 =0 b=a2 =0 d+aa+b d 4πE0 4πe'20
7 球面镜像法 r10、r20是从q、q′到球面上点的距离 q′和b待定 取球面上的点分别位于A、B两点,可以得到确定q′ 、b的两个方程: ' 0 ' 0 q q da ab q q da ab + = − − + = + + = −= d a b q d a q 2 ' 0 4 ' 4 0 10 0 20 =+ r q r q πεπε d q q’ b r10 r20 A B 20 10 0 10 0 20 ' | | ' 0 4 4 q qq r da r q q πε πε r r =− =− − + = XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
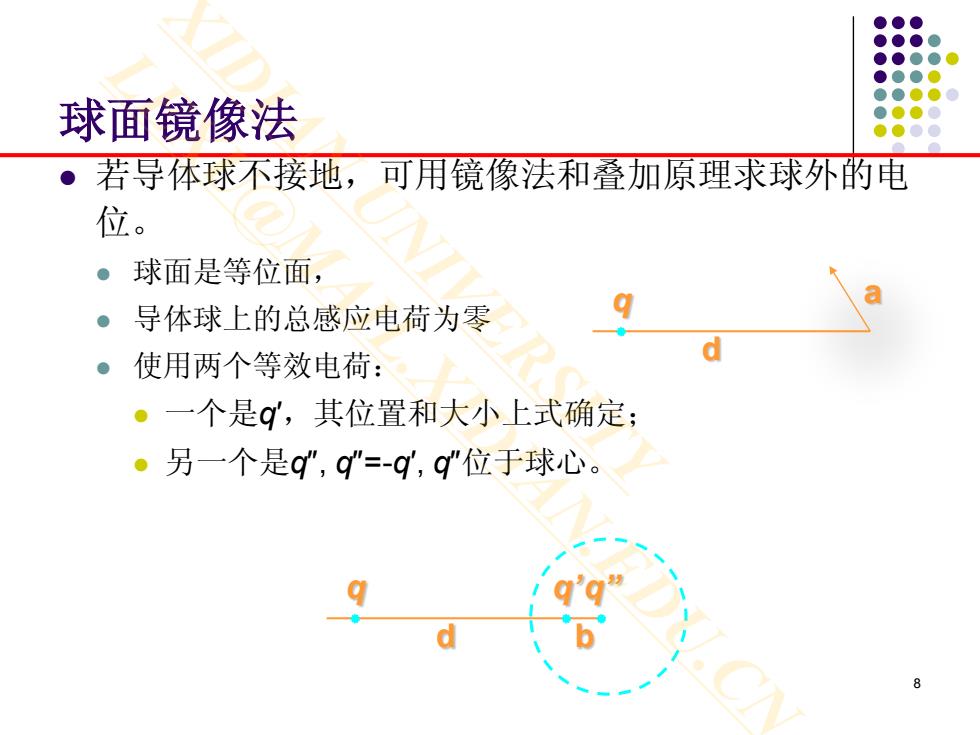
球面镜像法 。若导体球不接地,可用镜像法和叠加原理求球外的电 位。 ●球面是等位面, 。导体球上的总感应电荷为零 ●使用两个等效电荷: ·一个是g,其位置和大小上式确定; 。另一个是g”,q”=-q,g”位于球心
8 球面镜像法 若导体球不接地,可用镜像法和叠加原理求球外的电 位。 球面是等位面, 导体球上的总感应电荷为零 使用两个等效电荷: 一个是q′,其位置和大小上式确定; 另一个是q″, q″=-q′, q″位于球心。 d q q’ b q” a d q XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

球面镜像法 。如果导体球不接地,且带电荷Q, ●球面是等位面, 。导体球上的总电荷为Q a 。使用两个等效电荷: ·g位置和大小同上 ·q"的位置也在原点,但g”=Q-g,即g”=Q+qa/d
9 球面镜像法 如果导体球不接地,且带电荷Q, 球面是等位面, 导体球上的总电荷为Q 使用两个等效电荷: q′位置和大小同上 q″的位置也在原点,但q″=Q-q′, 即q″=Q+qa/d d q q’ b q” Q a d q XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

球面镜像法 ●Z1,Z2是关于以Z,为圆心R为半径的圆周对称点: ●复数描述: Z2 |31-2o‖22-20=R2 10 0
10 球面镜像法 Z1, Z2是关于以Z0为圆心R为半径的圆周对称点: 复数描述: 2 1 02 0 | || | zzz z R − −= Z0 Z1 Z2 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

球面镜像法 。例1空气中有两个半径相同(均等于)的导体球相切,试用球面 镜像法求该孤立导体系统的电容。 ·【解]用镜像法来确定导体所带总电荷: 无穷远处电位为零 导体面是等位面 C= U 11
11 球面镜像法 例1 空气中有两个半径相同(均等于a)的导体球相切,试用 球面 镜像法求该孤立导体系统的电容。 [解] 用镜像法来确定导体所带总电荷: 无穷远处电位为零 导体面是等位面 U q C = XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN