
Review 无源导电介质中麦克斯韦方程组及波动方程 V×H=oE+joEE Vx E=-jouH =0 7.i=0 7E=0 B=0 V2E+Y2E=0 VH+y2H=0 E=aEoe 00~ lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 2 Review 无源导电介质中麦克斯韦方程组及波动方程 0 0 H EjE E jH H E σ ωε ωµ ∇× = + ∇× = − ∇⋅ = ∇⋅ = −=−= ωε σ ε ω σ εε j j c 1 0 ˆ j z E aEe x − γ = 2 2 2 2 0 0 E E H H γ γ ∇+ = ∇+ = γβ α = − j 2 2 1 1 2 1 1 2 µε σ α ω ωε µε σ β ω ωε = +− = ++ θ η ωε σ ε µ ω σ ε µ η j c c j e j = −= − = − 2 1 1 0 ~ 4 π θ = c µ η ε < XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

Review n =a- 2 ne -20 COS0 导电媒质中的能量传播", B √e ■趋肤深度和表面电阻 6= ouo 对uo 电磁波的极化 传入导体的电磁 波实功率全部转 平面电磁波的极化形式 化为热损耗功率 电磁波极化特性的工程应用 E=( E.=Exm cos(ot-k+) E =Eym cos(ot-kz+) lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 3 Review 导电媒质中的能量传播 趋肤深度和表面电阻 电磁波的极化 平面电磁波的极化形式 电磁波极化特性的工程应用 1 2 2 12 1 1 1 p dz v dt ω β µε σ µε ωε = = = σ ωε α ωµσ π µσ δ f 121 === 传入导体的电磁 波实功率全部转 化为热损耗功率 ( ) ˆˆ x y j j jkz E aE aE e e x xm y ym φ φ − = + cos( ) cos( ) y ym y x xm x tEE kz tEE kz φω φω = +− = +− XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

Review ■电介质中均匀平面电磁波的相关参数可以近似为 B=OVEn= 21 ■良导体中,有关表达式可以用泰勒级数简化并近似表达为 20 a=B= .Up =2π 0(0+) lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 4 Review 电介质中均匀平面电磁波的相关参数可以近似为 良导体中,有关表达式可以用泰勒级数简化并近似表达为 ε µ ωβ µε η ε µσ α ≈ ≈ ,, ≈ 2 4 )1( 2 2 2, 2 , 2 π σ ωµ σ ωµ η ωµσ πλ µσ ω υ ωµσ βα j c p =+= ej == == XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

第21讲平面电磁波(川 介质色散 ■导体色散 ■相速和群速 ·平面电磁波向理想导体的垂直入射 ·平面电磁波向理想介质的垂直入射 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 5 第21讲 平面电磁波(III) 介质色散 导体色散 相速和群速 平面电磁波向理想导体的垂直入射 平面电磁波向理想介质的垂直入射 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

介质色散 ▣再看色散 ·色散名称来源于光学 。不同频率的光在同一介质中有不同的折射律,即具有不同的 相速度 ● 当可见光透过三棱镜时,三棱镜的另一边会出现赤橙黄绿青 蓝紫七色光谱 介质的色散是指介质的参数与频率有关 。波的色散是指波的相速与频率有关 ·一个任意波形的信号总可以看成是由许多时谐波叠加而成, 每一时谐波传播的相速是由介质参数μ、ε、σ确定。 若介质参数与频率有关,则是色散介质 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 6 介质色散 再看色散 • 色散名称来源于光学 • 不同频率的光在同一介质中有不同的折射律,即具有不同的 相速度 • 当可见光透过三棱镜时,三棱镜的另一边会出现赤橙黄绿青 蓝紫七色光谱 • 介质的色散是指介质的参数与频率有关 • 波的色散是指波的相速与频率有关 • 一个任意波形的信号总可以看成是由许多时谐波叠加而成, 每一时谐波传播的相速是由介质参数μ、ε、σ确定。 • 若介质参数与频率有关,则是色散介质 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

介质色散 轻离子 介质的色散 (电子) ·洛仑兹色散介质模型 分子 重离子 ·非极性分子: (原子核 ■电子和原子核电荷总量相等 ■正负电荷中心重合 ·对外不呈现电偶极矩 ■在外场作用下,正负电荷发生位移,其中心不再重 合,形成电偶极矩 ■假设位移r,电子电荷e 电子在外场作用下所受作用力为: =e(E+xB) lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 7 介质色散 介质的色散 • 洛仑兹色散介质模型 • 非极性分子: 电子和原子核电荷总量相等 正负电荷中心重合 对外不呈现电偶极矩 在外场作用下, 正负电荷发生位移,其中心不再重 合,形成电偶极矩 假设位移 r,电子电荷e 电子在外场作用下所受作用力为: 分子 重离子 (原子核) 轻离子 (电子) F eE v B = +× ( ) XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

介质色散 电子在外电场作用下的运动规律满足: 阻尼力 dr m +ar)=eE 弹性恢复力 ■设电场是时谐场,即ERe[Eme凹,) 则上式的解为: e 1m(0-o)+jo2 若单位体积内有N个电子,则 Ne2 m =Nerm= m (-o2)+joy lexu@mail.xidian.edu.cn 8
lexu@mail.xidian.edu.cn 8 介质色散 电子在外电场作用下的运动规律满足: 设电场是时谐场,即E=Re[Emejwt],则上式的解为: 若单位体积内有N个电子,则 2 2 2 0 ( ) d r dr m r eE dt dt ++ = γ ω 阻尼力 弹性恢复力 Re[ ] jwt m r re = 2 2 0 ( ) m m e E r m j ω ω ωγ = − + 2 2 2 0 ( ) m m m Ne E P Ner m j ω ω ωγ = = − + XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

介质色散 p=Wers】 Ne m(o-02)+j0y 单位体积内分子电矩的总和一极化强度 Ne2 1 Pm =EokeEm me。(0-o2)+j0y 极化率 6,=1+X。=1+ Ne2 (oj-o)-joy m60(@-02)+o27 相对介电常数 6=1+ Ne2 (0-o2) 波的传播速度 mso (@f-@2)2+@2y Ne2 ay m(-o22+o2元 波的衰减特性 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 9 介质色散 单位体积内分子电矩的总和—极化强度 2 2 2 0 ( ) m m m Ne E P Ner m j ω ω ωγ = = − + P E m em 0 = ε χ 2 2 2 0 0 1 ( ) e Ne m j χ ε ω ω ωγ = − + 极化率 相对介电常数 2 2 2 0 2 22 2 2 0 0 ( ) 1 1 ( ) r e Ne j m ω ω ωγ ε χ ε ω ω ωγ − − =+ =+ − + 2 2 2 0 2 22 2 2 0 0 2 2 22 2 2 0 0 ( ) 1 ( ) ( ) r r Ne m Ne m ω ω ε ε ω ω ωγ ωγ ε ε ω ω ωγ − ′ = + − + ′′ = − − + 波的传播速度 波的衰减特性 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
介质色散 Ne? (@-o) 8=1+ m(@-o2)2+o2y2 Ne? 00 mso (ap-02)2+02y 正常色散 反常色散 正常色散 自由原子的吸收频率几乎全部在紫外光谱区,一般介质的 折射率在从射频波谱直到紫外光谱区内都是大于1的: 反常色散区介电常数的虚部很大,能量被电离子吸收很多, 损耗很大 ■介电常数虚部随频率的变化曲线称为介质的吸收曲线。 lexu@mail.xidian.edu.cn 10
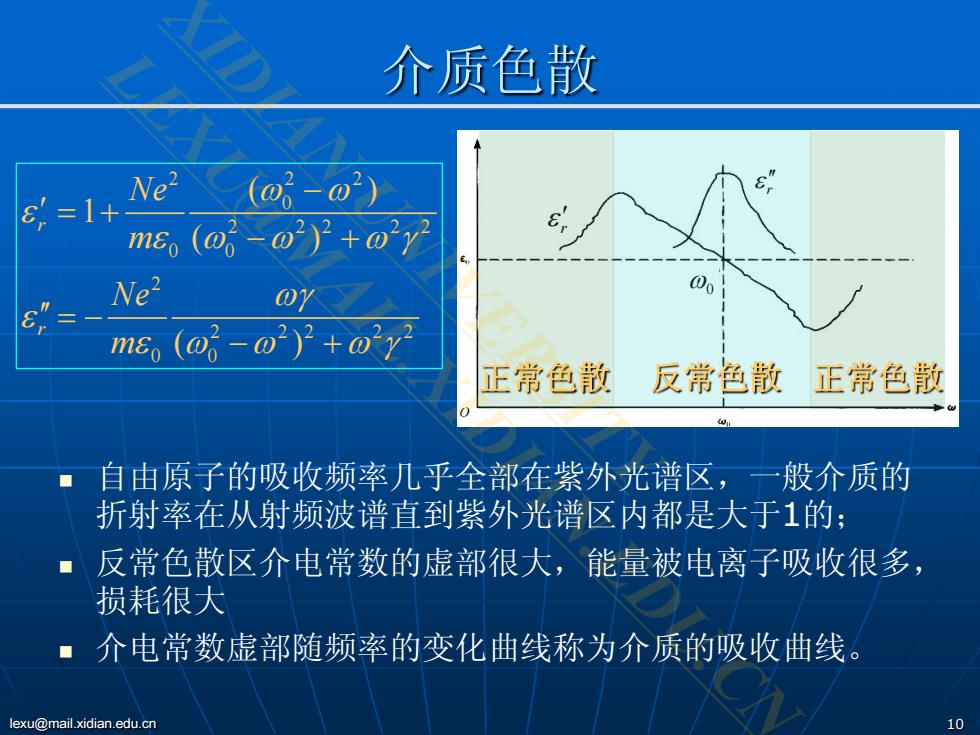
lexu@mail.xidian.edu.cn 10 介质色散 自由原子的吸收频率几乎全部在紫外光谱区,一般介质的 折射率在从射频波谱直到紫外光谱区内都是大于1的; 反常色散区介电常数的虚部很大,能量被电离子吸收很多, 损耗很大 介电常数虚部随频率的变化曲线称为介质的吸收曲线。 2 2 2 0 2 22 2 2 0 0 2 2 22 2 2 0 0 ( ) 1 ( ) ( ) r r Ne m Ne m ω ω ε ε ω ω ωγ ωγ ε ε ω ω ωγ − ′ = + − + ′′ = − − + r ε′ r ε′′ ω0 正常色散 反常色散 正常色散 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

导体色散 导体色散的模型 ·无外加电场时,导体的晶格上有固定的正离子,而在 其周围有运动的自由电子,它们处于平衡状态。 当有外加电场作用时,引起自由电子向外电场方向的 飘移,受到晶格上正离子的碰撞和阻挡,飘移电子的 动量转移到晶格点上变成正离子的热运动,同时电子 的运动也受到阻尼作用 d r d +q)=eE dt 。对于时谐场,即E-Re[E,me叮, 可以获得上式的稳态解, 从而获得导体的电导率 Ne2/m 当频率低于红外波段 Ne2 g+jw mg lexu@mail.xidian.edu.cn 11
lexu@mail.xidian.edu.cn 11 导体色散 导体色散的模型 • 无外加电场时,导体的晶格上有固定的正离子,而在 其周围有运动的自由电子,它们处于平衡状态。 • 当有外加电场作用时,引起自由电子向外电场方向的 飘移,受到晶格上正离子的碰撞和阻挡,飘移电子的 动量转移到晶格点上变成正离子的热运动,同时电子 的运动也受到阻尼作用 • 对于时谐场,即E=Re[Emejwt],可以获得上式的稳态解, 从而获得导体的电导率 2 2 ( ) d r dr m q eE dt dt + = 2 Ne m/ q j σ ω = + 2 Ne mq σ = 当频率低于红外波段 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN