
Review ·球面镜像法 ●柱面镜像法 ·介质平面镜像法 。其它方法简介 UNIVERSITY XIDIAN.EDU.CI 2011年6月10日星期五 lexu@mail.xidian.edu.cn 2
2011年6月10日星期五 lexu@mail.xidian.edu.cn 2 Review 球面镜像法 柱面镜像法 介质平面镜像法 其它方法简介 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

Review ·球面镜像法 DIA b= g'= d d 2011年6月10日星期五 lexu@mail.xidian.edu.cn q"=-q
2011年6月10日星期五 lexu@mail.xidian.edu.cn 3 Review 球面镜像法 a d q q q’ d b ' a q q d = − 2 a b d = a d q q q’ d b q” q″=-q′ a XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
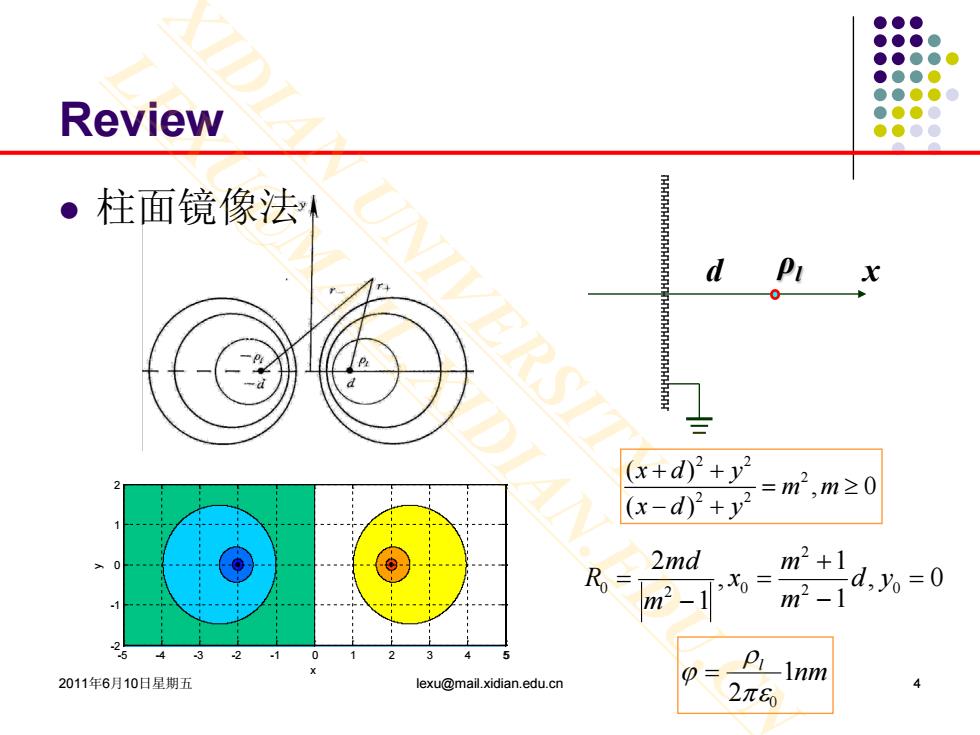
Review ·柱面镜像法 P (x+d2+y2 (x-d)2+y2 =m2,m20 2md Ro= m2+1 ,X0= d,%=0 1 m2-1 m2-1 3 3 2011年6月10日星期五 lexu@mail.xidian.edu.cn 0= PLInm 2π0
2011年6月10日星期五 lexu@mail.xidian.edu.cn 4 Review 柱面镜像法 d ρl x x y -5 -4 -3 -2 -1 0 1 2 3 4 55 -2 -1 0 1 2 2 2 2 2 2 ( ) , 0 ( ) xd y m m xd y + + = ≥ − + 0, 1 1 , 1 2 2 0 2 0 2 0 = − + = − = yd m m x m md R nm l 1 2πε0 ρ ϕ = XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
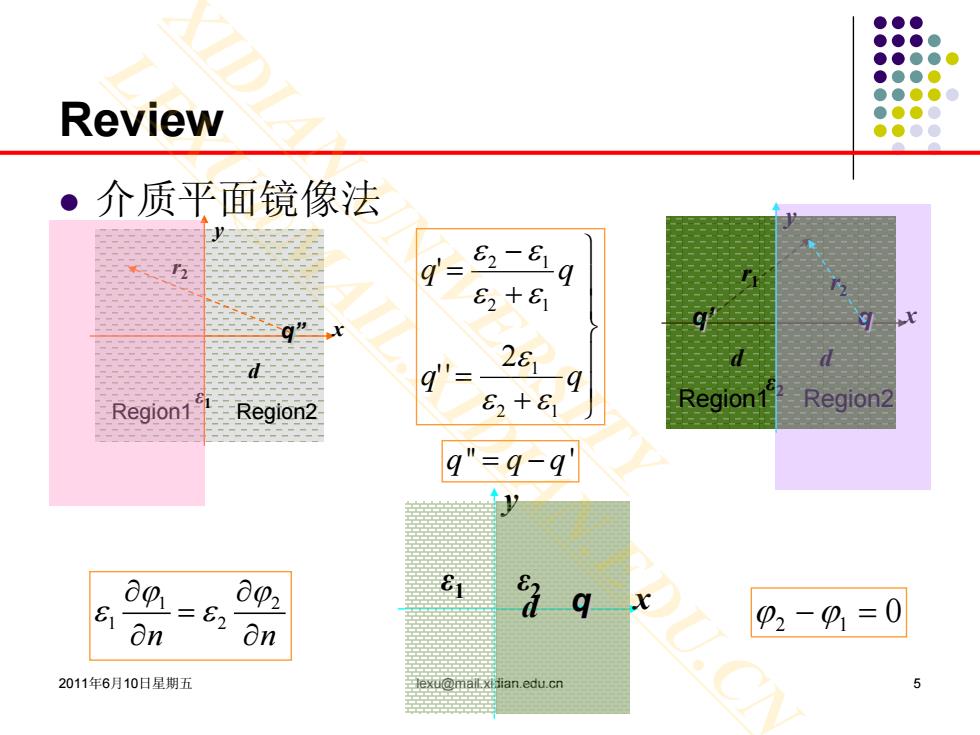
Review 。介质平面镜像法 g=-6q E2+8 q'= 26 9 Region1 Region2 82+81 Region1 Region2 q"=q-q' ∂0 002 On -6n0n dq x 02-0,=0 2011年6月10日星期五 mailxidian.edu.cn
2011年6月10日星期五 lexu@mail.xidian.edu.cn 5 Review 介质平面镜像法 d x y q ε2 q’ d r2 r1 Region1 Region2 d x y q” ε1 r2 Region1 Region2 x y d q ε1 ε2 1 2 1 2 n n ϕ ϕ ε ε ∂ ∂ = ∂ ∂ 0 ϕϕ 12 =− + = + − = q q qq 12 1 12 12 2 '' ' εε ε εε εε q qq '' ' = − XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

第12讲静态场的解(川) ·直角坐标系中的分离变量法 ·圆柱坐标系中的分离变量法 ● 球面坐标系中的分离变量法 IDIAN.EDU.C 2011年6月10日星期五 lexu@mail.xidian.edu.cn 6
2011年6月10日星期五 lexu@mail.xidian.edu.cn 6 第12讲 静态场的解(III) 直角坐标系中的分离变量法 圆柱坐标系中的分离变量法 球面坐标系中的分离变量法 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

直角坐标系中的分离变量法 。分离变量法是数学物理方法中最常用的一种方法; 。边界面需与一个适当的坐标系平面重合或分段重合 微分方程的解可以表示成为三个函数的乘积,且每个函 数仅是一个坐标的函数 ·分离变量法通过把微分方程化为常微方程求解 ·静态场中最常见的微分方程: V20=0 2011年6月10日星期五 lexu@mail.xidian.edu.cn
2011年6月10日星期五 lexu@mail.xidian.edu.cn 7 直角坐标系中的分离变量法 分离变量法是数学物理方法中最常用的一种方法; 边界面需与一个适当的坐标系平面重合或分段重合 微分方程的解可以表示成为三个函数的乘积,且每个函 数仅是一个坐标的函数 分离变量法通过把微分方程化为常微方程求解 静态场中最常见的微分方程: 2 ∇ = ϕ 0 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

直角坐标系中的分离变量法 。在直角坐标系中,拉普拉斯方程为 a20,a20.a2p ax20y2T22 =0 ●设0可以表示为三个函数的乘积: p(x,y,=)=X(x)Y(y)Z(z) 。代入拉普拉斯方程: 42+4 d? =0 2011年6月10日星期五 lexu@mail.xidian.edu.cn
2011年6月10日星期五 lexu@mail.xidian.edu.cn 8 直角坐标系中的分离变量法 在直角坐标系中, 拉普拉斯方程为 设φ可以表示为三个函数的乘积: 代入拉普拉斯方程: 0 2 2 2 2 2 2 = ∂ ∂ + ∂ ∂ + ∂ ∂ zyx ϕϕϕ ϕ = zZyYxXzyx )()()(),,( 0 2 2 2 2 2 2 =++ dz Zd XY dy Yd XZ dx Xd YZ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
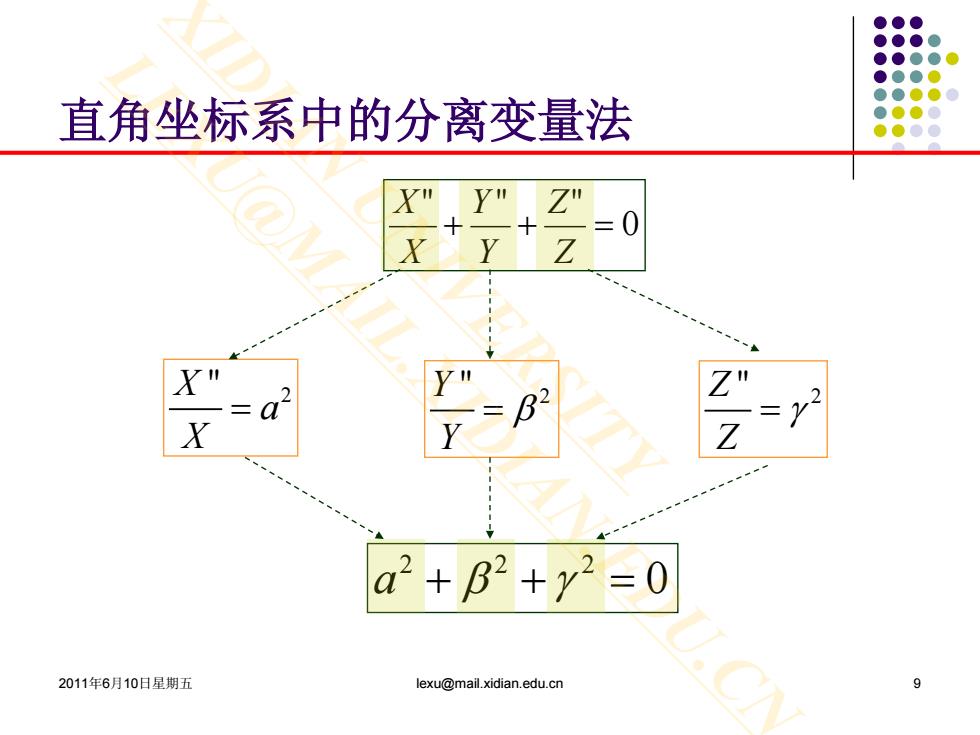
直角坐标系中的分离变量法 71 X a2+B2+y2=0 2011年6月10日星期五 lexu@mail.xidian.edu.cn
2011年6月10日星期五 lexu@mail.xidian.edu.cn 9 直角坐标系中的分离变量法 0 """ =++ Z Z Y Y X X X " 2 a X = 0 222 a γβ =++ Y " 2 Y = β Z " 2 Z = γ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

直角坐标系中的分离变量法 回顾二阶齐次线形微分方程的求解过程: 微分方程一般形式: y"+py'+gy=0 Step1:特征方程: r2+pr+q=0 。Step2:特征方程的根: 12= -p±Vp2-4g 2 Step3:选择相应的通解形式: 互异实根r1,2 y=Ce+Cex 相等实根r12 y=(C+C2x)e"x 2011年6月10 共轭复根r,2=a+j祁 @mail.xidiar y=e4 (C cos Bx+C2 sin Bx)
2011年6月10日星期五 lexu@mail.xidian.edu.cn 10 直角坐标系中的分离变量法 回顾二阶齐次线形微分方程的求解过程: 微分方程一般形式: Step1:特征方程: Step2:特征方程的根: Step3:选择相应的通解形式: y py qy ′′ ′ + += 0 2 r pr q + += 0 2 1,2 4 2 ppq r −± − = 互异实根r1,2 相等实根r1,2 共轭复根r1,2=α+jβ 1 2 1 2 rx r x y Ce Ce = + 1 1 2 ( ) r x y C Cxe = + 1 2 ( cos sin ) x y e C xC x α = β β + XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

直角坐标系中的分离变量法 =a X"-a2X=0 X 由二阶齐次线形微分方程求解过程可知: 。当a2=0时 X(x)=aox+bo 。当a20时,令=kx X(x)=c shk x+cchk,x X(x)=de kx+d,ekx 2011年6 xidian.edu.cn
2011年6月10日星期五 lexu@mail.xidian.edu.cn 11 直角坐标系中的分离变量法 由二阶齐次线形微分方程求解过程可知: 当α2=0时 当α20 时,令α=kx X " 2 a X = 2 X aX " 0 − = 2 1,2 r a = 00 )( += bxaxX )( = 1 sin x + 2 cos x xkaxkaxX jk x jk x x x )( 1 += 2ebebxX − 1 2 ( ) x x kx kx X x de de − X x c shk x c chk x ( ) = + 1 2 x x = + XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN