
电磁场与电磁波基础 主讲:徐乐 商安花子作枚大是
电磁场与电磁波基础 主讲:徐乐

第7讲静磁场(川) 、介质中的磁场 ·边界上的磁场 ·电感 磁场能量 。磁场力 2018年3月27日星期二 2
第7讲 静磁场(II) • 介质中的磁场 • 边界上的磁场 • 电感 • 磁场能量 • 磁场力 2018年3月27日星期二 2

介质中的磁场 ·真空中恒定电流激发恒定磁场 在外磁场作用下,磁介质内部产生磁化体电流,该电流同样激发 磁场 修正后的安培环路定律 Bd=H(I+)=to5(J+J)dS j=V×M ∮。Bdi=41+4,④Mi ∮.(月-M0)--7 H= B_M 40 lexu@mail.xidian.edu.cn 3
介质中的磁场 • 真空中恒定电流激发恒定磁场 • 在外磁场作用下,磁介质内部产生磁化体电流,该电流同样激发 磁场 • 修正后的安培环路定律 lexu@mail.xidian.edu.cn 3 0 0 () ( ) m m C S B dl I I J J dS ⋅= + = + ⋅ µ µ ∫ ∫ m J M =∇× 0 0 C C B dl I M dl ⋅= + ⋅ µ µ ∫ ∫ 0 ( ) C B M dl I µ − ⋅= ∫ 0 B H M µ = −

介质中的磁场 = B-M D=EE+P 40 -H称为磁场强度,单位是Am(安培/米)。 -显然:B=4,(i+M) 。 磁介质中的安培环路定律 -积分形式∮H.=1 -微分形式V×五=方 lexu@mail.xidian.edu.cn 4
介质中的磁场 – H称为磁场强度,单位是A/m(安培/米)。 – 显然: • 磁介质中的安培环路定律 – 积分形式 – 微分形式 lexu@mail.xidian.edu.cn 4 0 B H M µ = − D EP 0 = + ε 0 B HM = + µ ( ) C H dl I ⋅ = ∫ ∇× = H J

介质中的磁场 ·对于各向同性线性磁介质 B=4(H+M)=4(1+xm)H=4,4,i=ui -4,=1+Xm,是介质的相对磁导率,是一个无量纲数 =o4,是介质的磁导率,单位和真空磁导率相同,为 H/m(亨/米)。 铁磁材料的B和H的关系是非线性的,并且B不是H的单值函 数,会出现磁滞现象,其磁化率Xm的变化范围很大,可以达 到10量级。 所谓磁滞现象是指铁磁质磁化状 态的变化总是落后于外加磁场的 变化,在外磁场撤消后,铁磁质 仍能保持原有的部分磁性 5
介质中的磁场 • 对于各向同性线性磁介质 – μr =1+χm,是介质的相对磁导率,是一个无量纲数 – μ=μ0μr ,是介质的磁导率,单位和真空磁导率相同,为 H/m(亨/米)。 – 铁磁材料的B和H的关系是非线性的,并且B不是H的单值函 数,会出现磁滞现象,其磁化率χm的变化范围很大,可以达 到106量级。 lexu@mail.xidian.edu.cn 5 00 0 ( ) (1 ) B H M xH H H = += + = = µ µ µµ µ m r 所谓磁滞现象是指铁磁质磁化状 态的变化总是落后于外加磁场的 变化,在外磁场撤消后,铁磁质 仍能保持原有的部分磁性
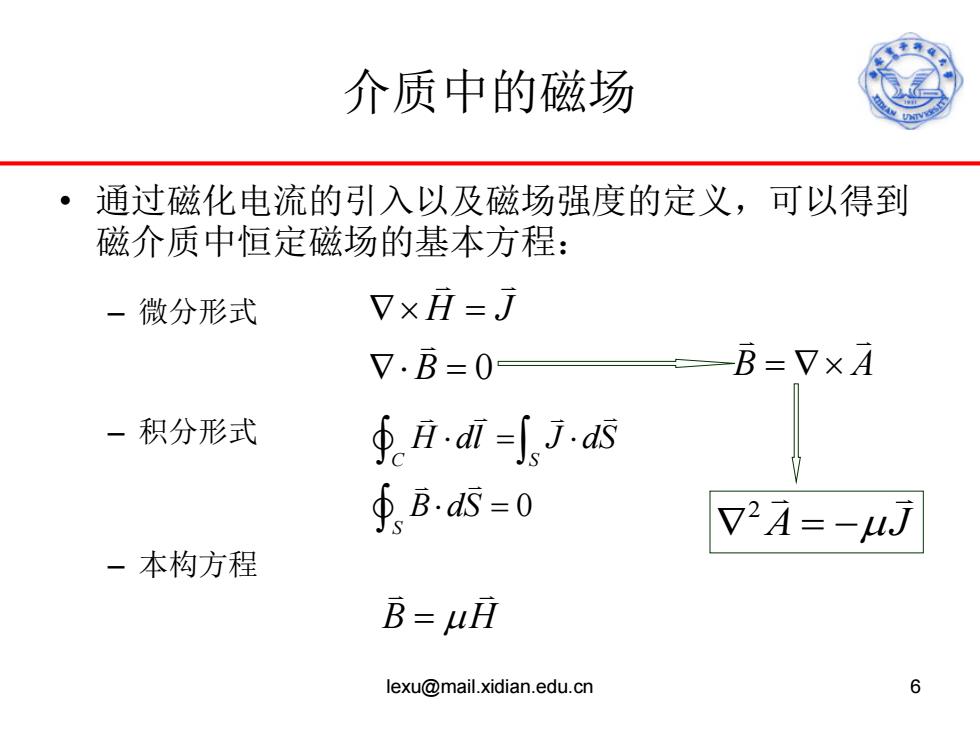
介质中的磁场 通过磁化电流的引入以及磁场强度的定义,可以得到 磁介质中恒定磁场的基本方程: -微分形式 7×i=j 7.B=0 B=V×A 一积分形式 ∮ii=jas ∮,B.s=0 V2A=-uJ 一本构方程 B=uHl lexu@mail.xidian.edu.cn 6
介质中的磁场 • 通过磁化电流的引入以及磁场强度的定义,可以得到 磁介质中恒定磁场的基本方程: – 微分形式 – 积分形式 – 本构方程 lexu@mail.xidian.edu.cn 6 0 H J B ∇× = ∇⋅ = 0 C S S H dl J dS B dS ⋅= ⋅ ⋅ = ∫ ∫ ∫ B H = µ 2 ∇ =− A J µ B A =∇×

介质中的磁场 ·例一导体圆柱半径为a,均匀分布电流/,柱外填充均匀 磁介质,磁导率为,求柱外的磁感应强度。 [解]无磁介质时磁场为柱对称,放入均匀磁介质,其磁化 情况也必为柱对称,所以总磁场仍为柱对称。且磁场 与z无关。做如图所示闭合路径1,则: fH-di=1 H.2πr=I H= 16 2πr B==HL 2πr lexu@mail.xidian.edu.cn
介质中的磁场 • 例 一导体圆柱半径为a,均匀分布电流I,柱外填充均匀 磁介质,磁导率为μ,求柱外的磁感应强度。 • [解]无磁介质时磁场为柱对称,放入均匀磁介质,其磁化 情况也必为柱对称,所以总磁场仍为柱对称。且磁场 与z无关。做如图所示闭合路径l,则: lexu@mail.xidian.edu.cn 7 H dl I l ⋅ = ∫ H ⋅ 2π r = I θ π ˆ 2 r I H = θ π µ µ ˆ 2 r I B = H =

边界上的磁场 ·如同静电场和恒定电流场, 磁场在经过磁介质的界面 后也会发生突变。 ·场矢量在不同介质的界面上的变化规律叫做边界条件 ·分析不连续性处的特性往往使用描述场分布的积分方 程 。 恒定磁场的边界条件研究磁场强度及磁感应强度在界 面两侧的关系。 lexu@mail.xidian.edu.cn 8
边界上的磁场 • 如同静电场和恒定电流场,磁场在经过磁介质的界面 后也会发生突变。 • 场矢量在不同介质的界面上的变化规律叫做边界条件 • 分析不连续性处的特性往往使用描述场分布的积分方 程 • 恒定磁场的边界条件研究磁场强度及磁感应强度在界 面两侧的关系。 lexu@mail.xidian.edu.cn 8
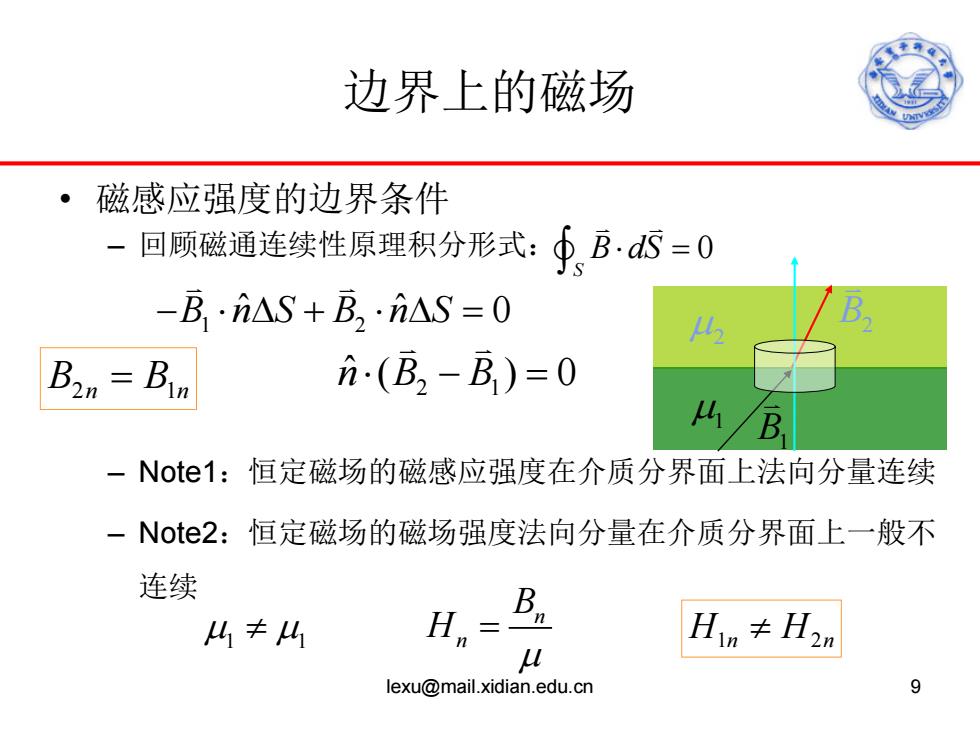
边界上的磁场 。1 磁感应强度的边界条件 -回顾磁通连续性原理积分形式:∮,BS=0 -B·n△S+B,·n△S=0 n(B2-B)=0 /B -Note1:恒定磁场的磁感应强度在介质分界面上法向分量连续 -Note2:恒定磁场的磁场强度法向分量在介质分界面上一般不 连续 凸1丰4 Hn≠H2n u lexu@mail.xidian.edu.cn 9
边界上的磁场 • 磁感应强度的边界条件 – 回顾磁通连续性原理积分形式: – Note1:恒定磁场的磁感应强度在介质分界面上法向分量连续 – Note2:恒定磁场的磁场强度法向分量在介质分界面上一般不 连续 lexu@mail.xidian.edu.cn 9 0 S B dS ⋅ = ∫ µ1 µ2 B1 B2 1 2 − ⋅∆ + ⋅∆ = B nS B nS ˆ ˆ 0 B2n = B1n 2 1 nB B ˆ ⋅−= ( )0 n n B H µ = µ µ 1 1 ≠ H H 1 2 n n ≠

边界上的磁场 磁场强度的边界条件 一在场论中,凡用闭合回路积分表述基本方程的场量,它的边 界条件一定以切向分量描述。 一回顾安培环路定律积分形式: ∮Hdl=js (i21-i-i)l=∫、j. 凸 ∫j=jbM 1.(i2-i)△1=Js·b△1 lexu@mail.xidian.edu.cn 10
边界上的磁场 • 磁场强度的边界条件 – 在场论中,凡用闭合回路积分表述基本方程的场量,它的边 界条件一定以切向分量描述。 – 回顾安培环路定律积分形式: lexu@mail.xidian.edu.cn 10 C S H dl J dS ⋅= ⋅ ∫ ∫ µ1 µ2 H1 H2 2 1 ˆ ˆ ( ) S H l H l l J dS ⋅ − ⋅ ∆= ⋅ ∫ S S J dS J b l ⋅ = ⋅∆ ∫ 2 1 ˆ ( ) S l H H l J bl ⋅ − ∆= ⋅∆