
Review 电流和电流密度;欧姆定律的微分形式、焦耳定律的微 分形式;电流连续性方程、恒定电场的散度;电动势、 恒定电场的旋度;恒定电场的基本方程;恒定电场的边 界条件;静场比拟法 。基本要求 。熟练掌握电流的分类、电流密度的定义。 掌握电荷守恒定律、欧姆定律微分形式、焦耳定律、 恒定电流场基本方程和边界条件。 ·重点、难点 。重点:电荷守恒定律、欧姆定律的微分形式、焦耳 定律、恒定电流场的基本方程和边界条件的数学表 达式及其含意。 难点:恒定电流场静电场的比拟、漏电阻计算
lexu@mail.xidian.edu.cn 2 Review 电流和电流密度;欧姆定律的微分形式、焦耳定律的微 分形式;电流连续性方程、恒定电场的散度;电动势、 恒定电场的旋度;恒定电场的基本方程;恒定电场的边 界条件;静场比拟法 基本要求 熟练掌握电流的分类、电流密度的定义。 掌握电荷守恒定律、欧姆定律微分形式、焦耳定律、 恒定电流场基本方程和边界条件。 重点、难点 重点:电荷守恒定律、欧姆定律的微分形式、焦耳 定律、恒定电流场的基本方程和边界条件的数学表 达式及其含意。 难点:恒定电流场与静电场的比拟、漏电阻计算 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

Review 电流密度 (( 。电荷守恒定律 v.j+4p 二0 dt 。欧姆定律 U=RI j()=σF) ●焦耳定律 P=UI p=J.E 。恒定电流场的基本方程 ∮j=0 7j=0 ·恒定电场的边界条件 ∮,E-di=0 V×E=0 。静电比拟法 n(j2-J)=0 i×(E2-E)=0 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 3 Review 电流密度 电荷守恒定律 欧姆定律 焦耳定律 恒定电流场的基本方程 恒定电场的边界条件 静电比拟法 ( ) ( ) 0 lim ˆ S I ∆ → S ∆ = ∆ Jr nr 0 d J dt ρ ∇⋅ + = ( ) ( ) rErJ U RI = = σ P = UI p JE = ⋅ 0 0 S l J dS E dl ⋅ = ⋅ = ∫ ∫ 0 0 J E ∇⋅ = ∇× = 2 1 nJ J ˆ⋅−= ( )0 2 1 nE E ˆ ×−= ( )0 V S d J ds dv dt ρ ⋅ =− ∫ ∫ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

第7讲恒定电流磁场 ·磁感应强度 。磁通连续性原理 ●安培环路定律 IVERSITY ·恒定磁场的基本方程 ●矢量磁位 KIDIAN.ED lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 4 第7讲 恒定电流磁场 磁感应强度 磁通连续性原理 安培环路定律 恒定磁场的基本方程 矢量磁位 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

磁感应强度 。场的产生 ●静止电荷在周围激发电场 。运动电荷(电流)在周围激发电场和磁场 。场的作用力 。电场对静止或运动电荷都施加以平行于电场的作用力 。磁场仅对运动电荷施加作用力,方向垂直于磁场 ·场的描述 。电场:电场强度E 。磁场:磁感应强度B ●1 恒定电流或永磁体产生的磁场不随时间变化,称为恒 定磁场,也称静磁场 exu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 5 磁感应强度 场的产生 静止电荷在周围激发电场 运动电荷(电流)在周围激发电场和磁场 场的作用力 电场对静止或运动电荷都施加以平行于电场的作用力 磁场仅对运动电荷施加作用力,方向垂直于磁场 场的描述 电场:电场强度E 磁场:磁感应强度B 恒定电流或永磁体产生的磁场不随时间变化,称为恒 定磁场,也称静磁场 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
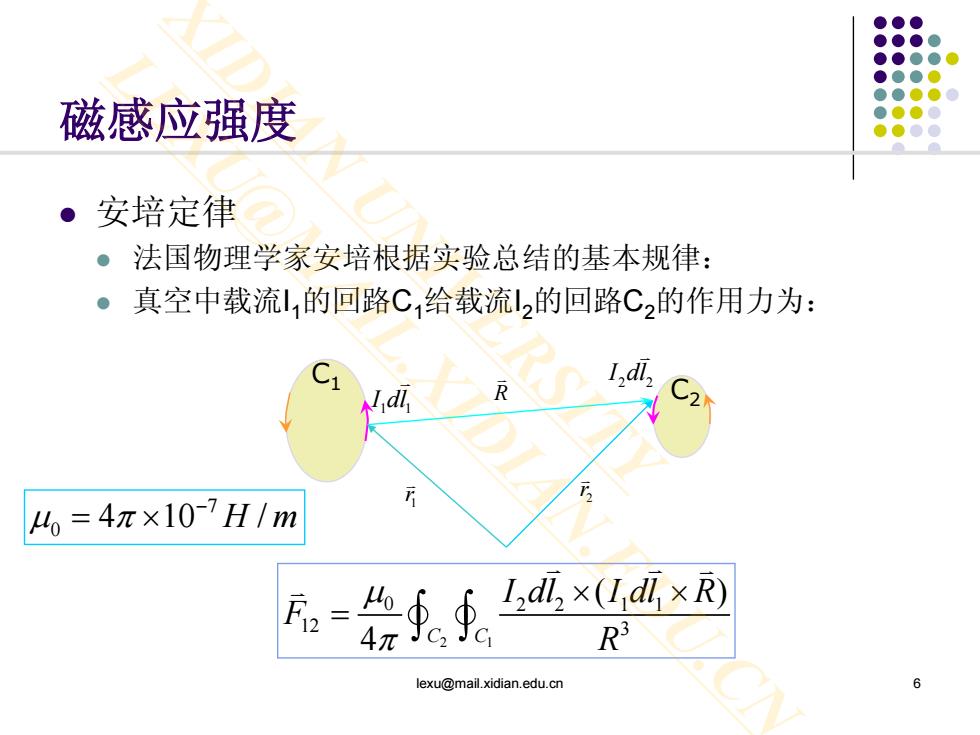
磁感应强度 ●安培定律 。法国物理学家安培根据实验总结的基本规律: 。真空中载流的回路C给载流l2的回路C,的作用力为: d 4=4π×10-7H1m F=重dh×Ld×用 4πJC2JC R lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 6 磁感应强度 安培定律 法国物理学家安培根据实验总结的基本规律: 真空中载流I1的回路C1给载流I2的回路C2的作用力为: 2 1 0 2 2 11 12 3 ( ) 4 C C I dl I dl R F R µ π × × = ∫ ∫ C2 2 2 I dl C1 1 1 I dl R 1 r 2r 7 0 µ π4 10 / H m − = × XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

磁感应强度 ●1 两闭合载流回路间的作用力可以理解为,第一个回路在 空间产生磁场,第二个回路在这个磁场中受力 F=∮。1,dl,× Id×R R B= Idl×F ·[定义] ·Note1:该式称为毕奥-萨伐尔定律 ●Note2:B为载流回路在r处产生的磁感应强度 。Note3:单位T(特斯拉),也用Wbm2(韦/米2) Iexu@mail.xidian.edu.cn 7
lexu@mail.xidian.edu.cn 7 磁感应强度 两闭合载流回路间的作用力可以理解为,第一个回路在 空间产生磁场,第二个回路在这个磁场中受力 [定义] Note1:该式称为毕奥-萨伐尔定律 Note2:B为载流回路在r处产生的磁感应强度 Note3:单位T(特斯拉),也用Wb/m2(韦/米2) 2 1 0 1 1 12 2 2 3 C C 4 u I dl R F I dl π R × = × ∫ ∫ 1 0 1 1 3 4 C I dl R B R µ π × = ∫ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

磁感应强度 ·若电流不是线电流而是具有体分布的电流J,则 ·线电流元模型Id还原成为分布于体积元dV'的真实 体电流分布模型: Idl J(r')dsdl =J(r')dsdl J(r')dv' 。体分布电流系统的毕萨定律: B)=么「 4πJ R Ea' 面分电流系统的比萨定律:上女)xR透 P3 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 8 磁感应强度 若电流不是线电流而是具有体分布的电流J,则 线电流元模型Idl还原成为分布于体积元dV’的真实 体电流分布模型: 体分布电流系统的毕萨定律: 面分布电流系统的比萨定律: 0 3 ( ') ( ) ' 4 V Jr R B r dV R µ π × = ∫ Idl J r dsdl J r dsdl J r dV = = = ( ') ( ') ( ') ' 0 3 ( ') ( ) ' 4 S S Jr R B r dS R µ π × = ∫ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

磁感应强度 。磁场对运动电荷的作用力 。置于磁场中载流为的线回路受到的磁场力: F=∮IdI xB 电流元ld在外磁场受力: dF Idll x B 。设dt时间内电荷走过距离dl=vdt,v为电荷运动速度, 且截面积dS,长度d的体积元电量为dg,则: df=IdlxB=dldl×B=d×B dt ●以速度v运动,电量q的点电荷受外磁场作用力F=q吓×B
lexu@mail.xidian.edu.cn 9 磁感应强度 磁场对运动电荷的作用力 置于磁场中载流为I的线回路受到的磁场力: 电流元Idl在外磁场受力: 设dt时间内电荷走过距离dl=vdt,v为电荷运动速度, 且截面积dS,长度dl的体积元电量为dq,则: 以速度v运动,电量q的点电荷受外磁场作用力: l F Idl B = × ∫ dF Idl B = × dq dF Idl B vdt B dqv B dt = ×= ×= × F qv B = × XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

磁感应强度 F=q啦xB ·Note1:此公式不仅适用于传导电流的运动电荷也适用于 运流电流中的运动电荷。 ·Note2:作用力同时垂直于磁感应强度B和粒子运动速度v 。Note3:只作用于运动带电粒子,且永不对带电粒子做功 。Note4: 若电量为q的运动电荷所在空间同时存在电场和磁 场,则它所受的电场力和磁场力的总和即为洛仑 兹力: 7=q(E+v×B) lexu@mail.xidian.edu.cn 10
lexu@mail.xidian.edu.cn 10 磁感应强度 Note1:此公式不仅适用于传导电流的运动电荷也适用于 运流电流中的运动电荷。 Note2:作用力同时垂直于磁感应强度B和粒子运动速度v Note3:只作用于运动带电粒子,且永不对带电粒子做功 Note4:若电量为q的运动电荷所在空间同时存在电场和磁 场,则它所受的电场力和磁场力的总和即为洛仑 兹力: F qv B = × F qE v B = +× ( ) XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

磁感应强度 ·例1求载流的有限长直导线外任一点的磁场。 [解]取直导线的中心为坐标原点, 导线和z轴重合》 在圆柱坐标中计算。 B()=∮ Idl 'x R R=F一引 2 4πcR (r,0,e) 由对称性可知磁场与坐标0无关 R 不失一般性,将场点取在0=0, 场点坐标为(,0,z) a 源点坐标为(0,0,) z'=z-rtana dl '=a.dz' dz'=rsec2 a R=rseca dl'xR=ade'x[ra,+(z-=)a.]=-agr"sec"a lexu@mail.xidian.edu.cn 11
lexu@mail.xidian.edu.cn 11 磁感应强度 例1 求载流I的有限长直导线外任一点的磁场。 [解] 取直导线的中心为坐标原点,导线和z轴重合, 在圆柱坐标中计算。 由对称性可知磁场与坐标φ无关 不失一般性,将场点取在φ =0, 场点坐标为(r, 0, z) 源点坐标为(0,0,z′) 0 3 ' ( ) 4 C Idl R B r R µ π × = ∫ 2 ' tan ' sec sec z zr dz r R r α α α = − = = ˆˆr z r ra za = + ' ' ˆz r za = Rrr = − ' ' ' ˆz dl a dz = 2 2 ' ' [ ( ') ] sec ˆˆˆˆ zr z dl R a dz ra z z a a r × = × + − =− φ α XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN