
电磁场与电磁波基础 主讲:徐乐 商安着子种找大整
电磁场与电磁波基础 主讲:徐乐

Review ·电流密度 -盟岩 ·电荷守恒定律 = V.J+dp=0 dt ·欧姆定律 U=RI 万F)=ōE(F) ·焦耳定律 P=UI p=J.E ·恒定电流场的基本方程 ∮s=0 7.j=0 ∮Ei=0 7×E=0 ·恒定电场的边界条件 ·静电比拟法 n(J2-j)=0 nx(E2-E)=0 lexu@mail.xidian.edu.cn
Review • 电流密度 • 电荷守恒定律 • 欧姆定律 • 焦耳定律 • 恒定电流场的基本方程 • 恒定电场的边界条件 • 静电比拟法 lexu@mail.xidian.edu.cn 2 ( ) ( ) 0 lim ˆ S I ∆ → S ∆ = ∆ Jr nr 0 d J dt ρ ∇⋅ + = J (r) E(r) U RI = = σ P = UI p JE = ⋅ 0 0 S l J dS E dl ⋅ = ⋅ = ∫ ∫ 0 0 J E ∇⋅ = ∇× = 2 1 nJ J ˆ⋅−= ( )0 2 1 nE E ˆ ×−= ( )0 V S d J ds dv dt ρ ⋅ =− ∫ ∫
磁场? H Field [A/m] 4,1710E+081 ,8503E+001 .5296E 08, 3.2089E+001 2,8882E+031 2,5675E+001 2.2468E+001 1,9261E+031 1.6054E+83 1.2847E+60 9,6395E+080 5,4324E+0 3.2253E+0e 1.8203E-002 Phase nden l
磁场? 3

磁场 ·场的产生 一静止电荷在周围激发电场 一运动电荷(电流)在周围激发电场和磁场 ·场的作用力 一电场对静止或运动电荷都施加以平行于电场的作用力 一磁场仅对运动电荷施加作用力,方向垂直于磁场 ·场的描述 一电场:电场强度E 一磁场:磁感应强度B ·恒定电流或永磁体产生的磁场不随时间变化,称为恒 定磁场,也称静磁场 lexu@mail.xidian.edu.cn 4
磁场 • 场的产生 – 静止电荷在周围激发电场 – 运动电荷(电流)在周围激发电场和磁场 • 场的作用力 – 电场对静止或运动电荷都施加以平行于电场的作用力 – 磁场仅对运动电荷施加作用力,方向垂直于磁场 • 场的描述 – 电场:电场强度E – 磁场:磁感应强度B • 恒定电流或永磁体产生的磁场不随时间变化,称为恒 定磁场,也称静磁场 lexu@mail.xidian.edu.cn 4

第6讲恒定电流磁场() ·真空中的场 一安培定律 一通量与散度 一环量与旋度 一矢量磁位 ·介质中的场 一磁偶极子 lexu@mail.xidian.edu.cn 5
第6讲 恒定电流磁场(I) • 真空中的场 – 安培定律 – 通量与散度 – 环量与旋度 – 矢量磁位 • 介质中的场 – 磁偶极子 lexu@mail.xidian.edu.cn 5
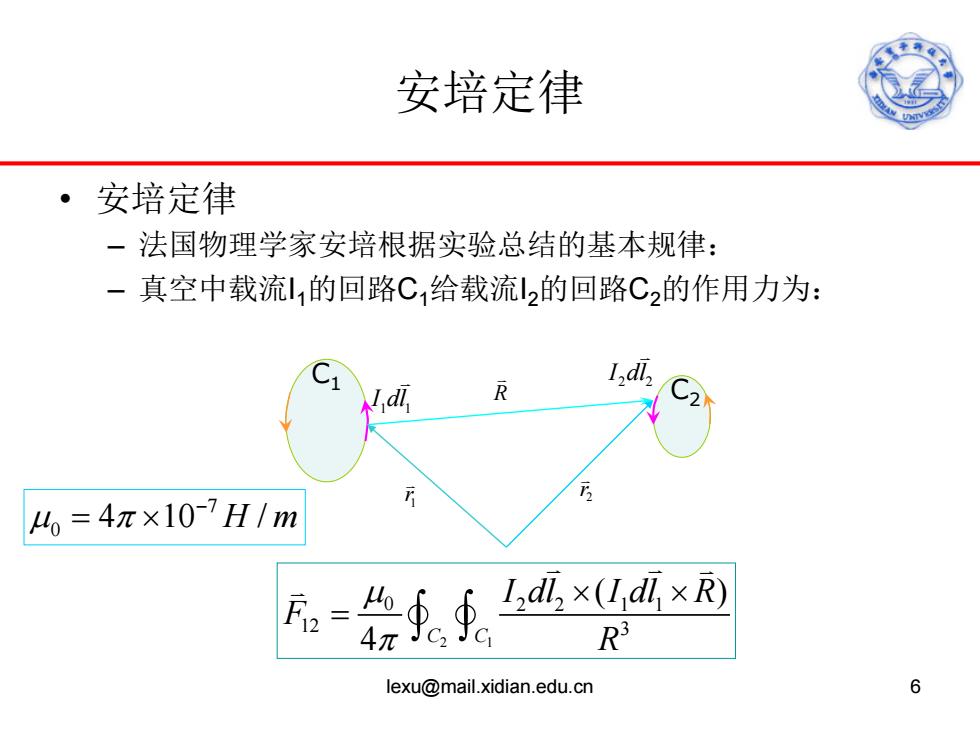
安培定律 安培定律 一法国物理学家安培根据实验总结的基本规律: 一真空中载流l1的回路C1给载流l2的回路C,的作用力为: 4=4π×10-7H/m F2=∮∮.I×☑×R 4πC2JC R3 lexu@mail.xidian.edu.cn 6
安培定律 • 安培定律 – 法国物理学家安培根据实验总结的基本规律: – 真空中载流I1的回路C1给载流I2的回路C2的作用力为: lexu@mail.xidian.edu.cn 6 2 1 0 2 2 11 12 3 ( ) 4 C C I dl I dl R F R µ π × × = ∫ ∫ C2 2 2 I dl C1 1 1 I dl R 1 r 2r 7 0 µ π4 10 / H m − = ×

安培定律 ·两闭合载流回路间的作用力可以理解为,第一个回路在 空间产生磁场,第二个回路在这个磁场中受力 a=∮,,× Idl xR 4πGR3 ·[定义] B=%∮n4xR R3 ·Note1:该式称为毕奥-萨伐尔定律 ·Note2:B为载流回路在r处产生的磁感应强度 ·Note3:单位T(特斯拉),也用Wbm2(韦/米2) lexu@mail.xidian.edu.cn
安培定律 • 两闭合载流回路间的作用力可以理解为,第一个回路在 空间产生磁场,第二个回路在这个磁场中受力 • [定义] • Note1:该式称为毕奥-萨伐尔定律 • Note2:B为载流回路在r处产生的磁感应强度 • Note3:单位T(特斯拉),也用Wb/m2(韦/米2) lexu@mail.xidian.edu.cn 7 2 1 0 1 1 12 2 2 3 C C 4 u I dl R F I dl π R × = × ∫ ∫ 1 0 1 1 3 4 C I dl R B R µ π × = ∫

安培定律 ·若电流不是线电流而是具有体分布的电流J,则 -线电流元模型Id还原成为分布于体积元dW'的 真实体电流分布模型: Idl =J(r'dsdl =J(r'dsdl =J(r'dv' 一体分布电流系统的毕萨定律: R3 面分布电流系统的比萨定律:)'*5 4πJsR3 lexu@mail.xidian.edu.cn
安培定律 • 若电流不是线电流而是具有体分布的电流J,则 – 线电流元模型Idl还原成为分布于体积元dV’的 真实体电流分布模型: – 体分布电流系统的毕萨定律: – 面分布电流系统的比萨定律: lexu@mail.xidian.edu.cn 8 0 3 ( ') ( ) ' 4 V Jr R B r dV R µ π × = ∫ Idl J r dsdl J r dsdl J r dV = = = ( ') ( ') ( ') ' 0 3 ( ') ( ) ' 4 S S Jr R B r dS R µ π × = ∫

安培定律 ·磁场对运动电荷的作用力 -置于磁场中载流为的线回路受到的磁场力: F=④IdI xB -电流元Id在外磁场受力: dF Idl x B -设dt时间内电荷走过距离dl=vdt,v为电荷运动速度,且 截面积dS,长度dl的体积元电量为dg,则: dE=1al×B=dadixB=drxB dt -以速度v运动,电量q的点电荷受外磁场作用力:F=q下×B lexu@mail.xidian.edu.cn
安培定律 • 磁场对运动电荷的作用力 – 置于磁场中载流为I的线回路受到的磁场力: – 电流元Idl在外磁场受力: – 设dt时间内电荷走过距离dl=vdt,v为电荷运动速度,且 截面积dS,长度dl的体积元电量为dq,则: – 以速度v运动,电量q的点电荷受外磁场作用力: lexu@mail.xidian.edu.cn 9 l F Idl B = × ∫ dF Idl B = × dq dF Idl B vdt B dqv B dt = ×= ×= × F qv B = ×

安培定律 F=q币×B ·Note1:此公式不仅适用于传导电流的运动电荷也适用于 运流电流中的运动电荷。 ·Note2:作用力同时垂直于磁感应强度B和粒子运动速度v ·Note3:只作用于运动带电粒子,且永不对带电粒子做功 ·Note4:若电量为q的运动电荷所在空间同时存在电场和磁 场,则它所受的电场力和磁场力的总和即为洛仑 兹力: F=q(E+下×B) lexu@mail.xidian.edu.cn 10
安培定律 • Note1:此公式不仅适用于传导电流的运动电荷也适用于 运流电流中的运动电荷。 • Note2:作用力同时垂直于磁感应强度B和粒子运动速度v • Note3:只作用于运动带电粒子,且永不对带电粒子做功 • Note4:若电量为q的运动电荷所在空间同时存在电场和磁 场,则它所受的电场力和磁场力的总和即为洛仑 兹力: lexu@mail.xidian.edu.cn 10 F qv B = × F qE v B = +× ( )