黑体辐射实验 实验18黑体辐射实验 【实验原理】 任何物体只要其温度在绝对零度以上就可以向周围发射辐射,称之为温度辐射。黑体是一种 完全的温度辐射体,它吸收全部的入射光辐射而一点也不反射。黑体辐射能量的效率最高,仅与 温度有关,它的发射率是1,任何其它物体的发射率都小于1。 1.常用术语 )黑体:一种理想的辐射能源,是一种辐射仅取决于它的温度的辐射体,它在给定的温度下比 在同样温度下的任何实际物体辐射出更多的能量。故也称之为“完全辐射体”或“理想的温 度辐射体”或“普朗克辐射体”。 b)辐射度:也称为“辐射出射度”,简称“辐出度”。表面上一点的辐射度为该点表面元发出的 辐射通量除以该表面元的面积的商,单位是(瓦/米2), c)辐亮度:表示光源的表面元发出的,在给定方向的基准所确定的方向传播的辐射通量,除以 锥的立体角和表面元在垂直于给定方向的平面上的投影面积的乘积的商,单位是(瓦特/米? ·球面度)。 )色温:一个光源的色温就是辐射同一色品光的黑体的温度。 2。黑体辐射定律 1)黑体辐射的光谱分布一一普朗克定律 图18.1黑体的谱线亮度随波长的变化关系 普朗克定律叙述了黑体辐射的光谱分布。此定律用光谱辐射出射度E表示,其形式为: BarD (瓦特/米) (18.1) 式中,C=2xhC2=3.7415×1016(瓦特/米2),C2=chk=1.4388×102(米X开尔文),h是普朗 克常数,T为绝对温度, 111
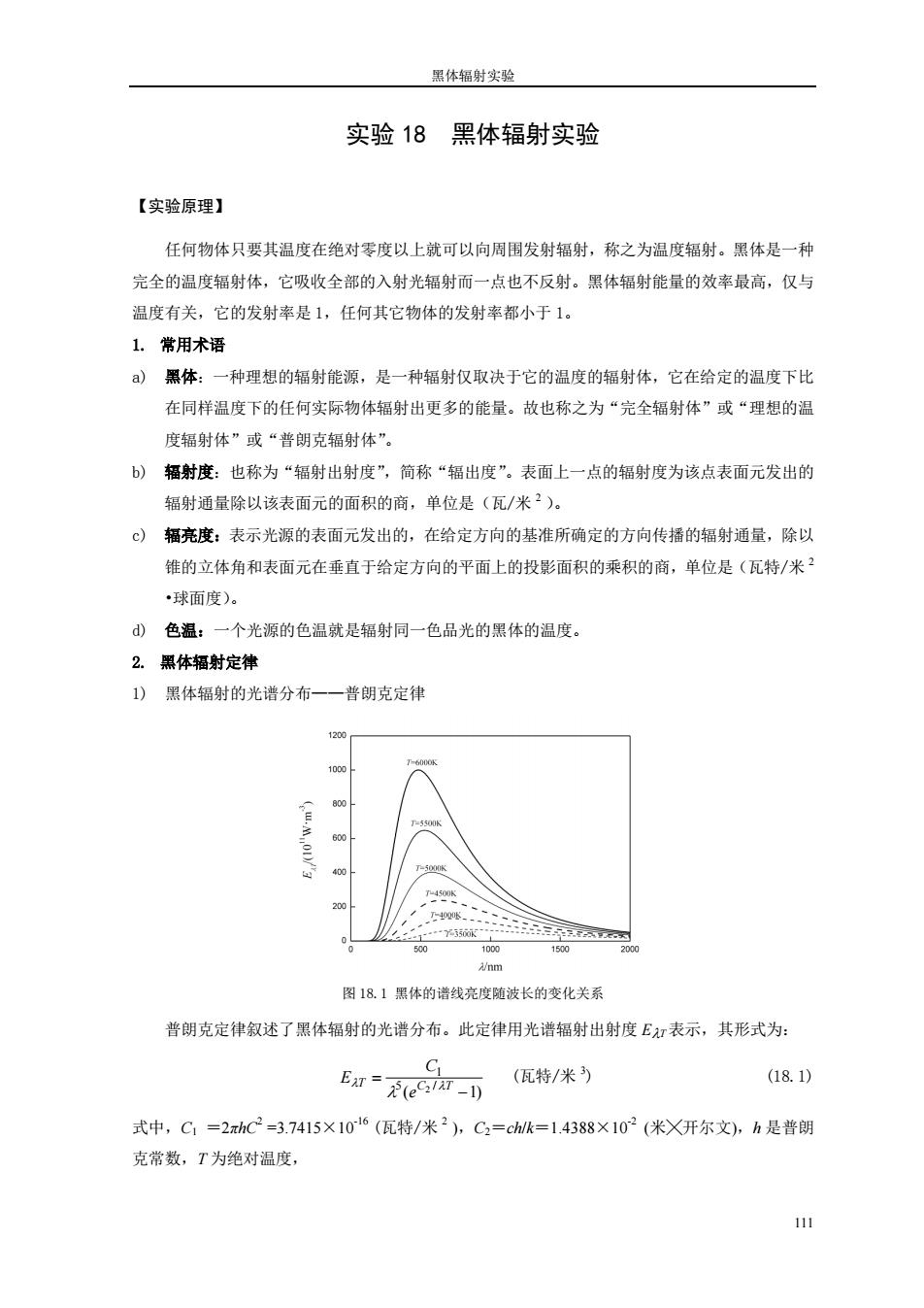
黑体辐射实验 111 实验 18 黑体辐射实验 【实验原理】 任何物体只要其温度在绝对零度以上就可以向周围发射辐射,称之为温度辐射。黑体是一种 完全的温度辐射体,它吸收全部的入射光辐射而一点也不反射。黑体辐射能量的效率最高,仅与 温度有关,它的发射率是 1,任何其它物体的发射率都小于 1。 1. 常用术语 a) 黑体:一种理想的辐射能源,是一种辐射仅取决于它的温度的辐射体,它在给定的温度下比 在同样温度下的任何实际物体辐射出更多的能量。故也称之为“完全辐射体”或“理想的温 度辐射体”或“普朗克辐射体”。 b) 辐射度:也称为“辐射出射度”,简称“辐出度”。表面上一点的辐射度为该点表面元发出的 辐射通量除以该表面元的面积的商,单位是(瓦/米 2 )。 c) 辐亮度:表示光源的表面元发出的,在给定方向的基准所确定的方向传播的辐射通量,除以 锥的立体角和表面元在垂直于给定方向的平面上的投影面积的乘积的商,单位是(瓦特/米 2 •球面度)。 d) 色温:一个光源的色温就是辐射同一色品光的黑体的温度。 2. 黑体辐射定律 1) 黑体辐射的光谱分布——普朗克定律 图 18.1 黑体的谱线亮度随波长的变化关系 普朗克定律叙述了黑体辐射的光谱分布。此定律用光谱辐射出射度 ET 表示,其形式为: ( 1) 5 / 1 2 T C T e C E (瓦特/米 3 ) (18.1) 式中,C1 =2πhC2 =3.7415×10-16 (瓦特/米 2 ),C2=ch/k=1.4388×10-2 (米╳开尔文),h 是普朗 克常数,T 为绝对温度

近代物理实验讲义 2)黑体辐射的积分表达式一—斯式藩一波尔兹曼定律 在从零到无穷大的波长范围内,积分普朗克公式,得到光谱辐射出射度E,的积分表达式, 其形式为: E,=Ed=o(瓦特/米2) (18.2) 式中,σ是斯忒潜-波尔兹曼常数,0=5.6697×108(瓦/米2·开尔文) 3)维恩位移定律 微分普朗克定理,求出辐射度最大时对应的波长mx,就得到了维恩位移定律。其形式为: (18.3) 式中,A=2.898×10(mK). 综上,斯式藩一波尔兹曼定律阐述了黑体的总辐射随绝对温度的四次幂而变化,其方程确定 了一个黑体从1cm面积进入半球空间里的总辐射量。维恩位移定律指明了对应每一温度下最大 辐射的波长。随温度的升高,绝对黑体光谱亮度的最大值的波长向短波方向移动。图18.1给出 了E杠随波长变化的图形。图中每条曲线最大值对应的波长就是元,曲线上标注的数据就是其 色温。如色温为6000K的黑体. -2898x10mK-0483m=483nm (18.40 6000K 3.光源 图18.2溴钨灯电源 金属钨的辐射近似于可见光波段内的黑体光谱能量分布。它的熔点高,可达到3650K,所以 钨可用来模拟黑体。 钨丝灯的总辐射度R可由下式求出: RT=EOT4 (18.5) 式中,为温度T时的总辐射系数,它是溴钨灯的辐射度与绝对黑体的辐射度之比,即 (18.6) 112
近代物理实验讲义 112 2) 黑体辐射的积分表达式——斯忒藩-波尔兹曼定律 在从零到无穷大的波长范围内,积分普朗克公式,得到光谱辐射出射度 ET 的积分表达式, 其形式为: 4 0 ET ET d T (瓦特/米 2 ) (18.2) 式中,是斯忒藩-波尔兹曼常数,=5.6697×10-8(瓦/米 2 •开尔文 4) 3) 维恩位移定律 微分普朗克定理,求出辐射度最大时对应的波长max,就得到了维恩位移定律。其形式为: T A max (18.3) 式中, A=2.898×10-3 (m·K)。 综上,斯忒藩-波尔兹曼定律阐述了黑体的总辐射随绝对温度的四次幂而变化,其方程确定 了一个黑体从 1cm 2 面积进入半球空间里的总辐射量。维恩位移定律指明了对应每一温度下最大 辐射的波长。随温度的升高,绝对黑体光谱亮度的最大值的波长向短波方向移动。图 18.1 给出 了 ET 随波长变化的图形。图中每条曲线最大值对应的波长就是max,曲线上标注的数据就是其 色温。如色温为 6000K 的黑体, m nm K m K 0.483 483 6000 2.898 10 3 max . (18.4) 3. 光源 图 18.2 溴钨灯电源 金属钨的辐射近似于可见光波段内的黑体光谱能量分布。它的熔点高,可达到 3650K,所以 钨可用来模拟黑体。 钨丝灯的总辐射度 RT 可由下式求出: 4 RT TT , (18.5) 式中,T为温度 T 时的总辐射系数,它是溴钨灯的辐射度与绝对黑体的辐射度之比,即 T T T E R ,或 BT T e 1 (18.6)
黑体辐射实验 式中B为常数,1.47×10。 钨丝灯的辐射光谱分布R为: Rir =8Eit = (18.7) e-1 溴钨灯的电源控制箱采用可调电流的稳压装置,通过调节电流值改变溴钨灯的色温。 【实验仪器】 LI口T s 图18.2光学系统原理图 S:入射狭缝S2:出射秩缝1S:出射狭缝ⅡG平面衍射光栅M,M,M:反射镜 M2,M:球面反射镜M6:深椭球镜L:滤光片T调制器P按收器件 S-1型黑体实验装置,由光橘单色仪、接收单元、溴钨灯、可调稳压溴钨灯光源、电源控 制箱以及计算机组成。其主要光学系统结构如图18.2所示。 1.光摄单色仪 光栅单色仪采用衍射光栅作为色散元件,它将被测辐射色散为其光谱以便测量,它主要由光 学系统、光栅驱动系统、狭缝机构、观察窗等组成。 光源发出的光束,进入入射狭缝S,后经反射镜M1反射到M,上,经M,反射成平行光束投 射到平面光栅G上,衍射后的平行光束经球面反射镜M成象在S,(或S:)上,进入S,后的光 束,经调制器T调制成80O后,再经M反射到深椭球镜M6上后成象到接收器P的把面上。 反射镜M是可旋转摆动的,经M反射后的成象光束除可直接投射到M、M6外,还可以通过 旋转M使反射后的光束成象到S,上。 2.接收单元 随着电子技术和电子仪器的高度发展,光辐射测量中多采用对红外辐射敏感的光电器件。本 实验装置采用PbS作接收单元,它对波长范围在800-2500nm的近红外光有较好的光谱响应。从 单色仪出缝1射出的单色光经信号调制器,调制成800z的频率信号被PS接收
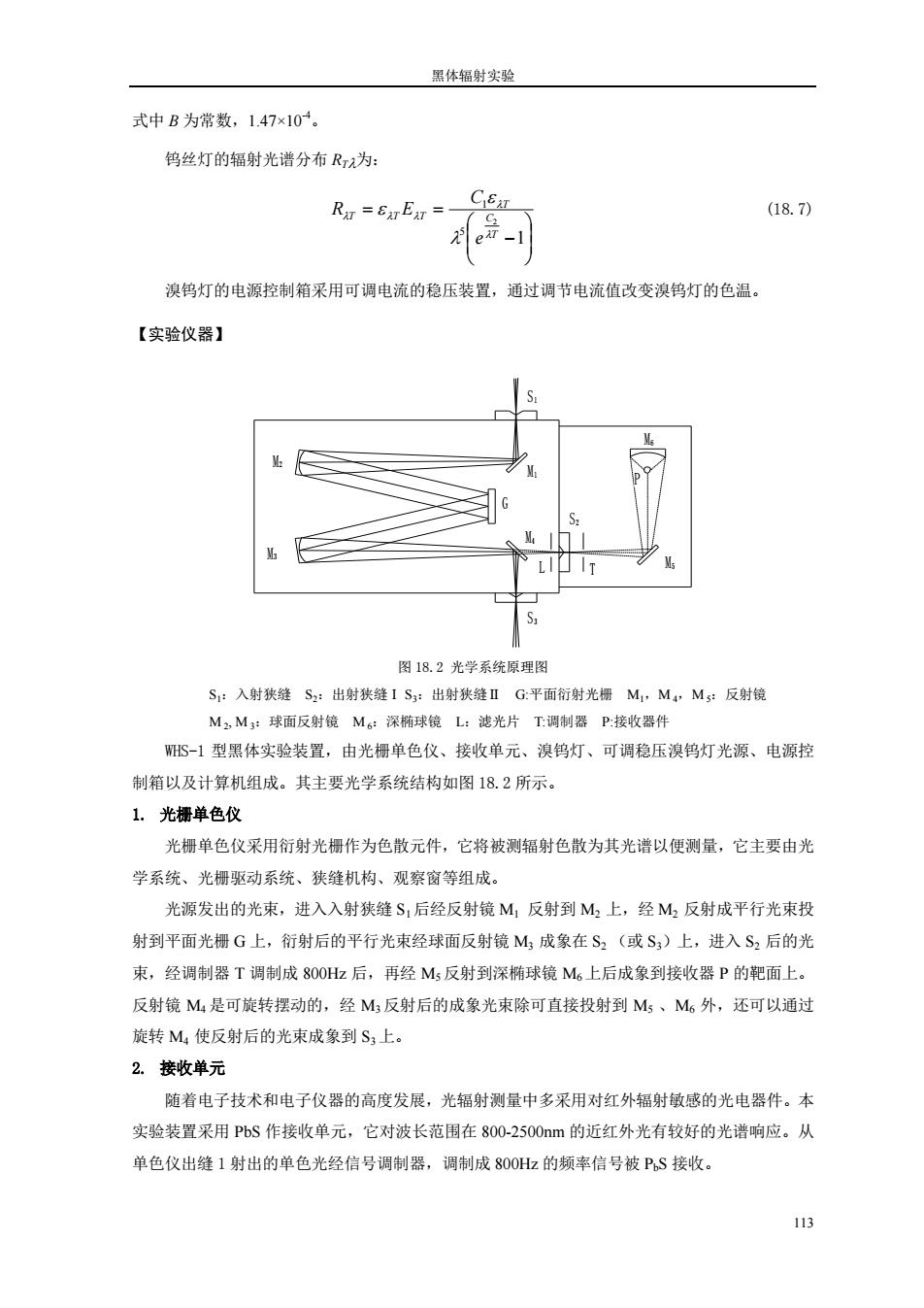
黑体辐射实验 113 式中 B 为常数,1.47×10-4。 钨丝灯的辐射光谱分布 RT为: 1 2 5 1 T C T T T T e C R E (18.7) 溴钨灯的电源控制箱采用可调电流的稳压装置,通过调节电流值改变溴钨灯的色温。 【实验仪器】 M6 S1 M1 M2 G M3 M4 S3 L S2 T M5 P 图 18.2 光学系统原理图 S1:入射狭缝 S2:出射狭缝Ⅰ S3:出射狭缝Ⅱ G:平面衍射光栅 M1,M 4,M 5:反射镜 M 2 , M 3:球面反射镜 M 6:深椭球镜 L:滤光片 T:调制器 P:接收器件 WHS-1 型黑体实验装置,由光栅单色仪、接收单元、溴钨灯、可调稳压溴钨灯光源、电源控 制箱以及计算机组成。其主要光学系统结构如图 18.2 所示。 1. 光栅单色仪 光栅单色仪采用衍射光栅作为色散元件,它将被测辐射色散为其光谱以便测量,它主要由光 学系统、光栅驱动系统、狭缝机构、观察窗等组成。 光源发出的光束,进入入射狭缝 S1后经反射镜 M1 反射到 M2 上,经 M2 反射成平行光束投 射到平面光栅 G 上,衍射后的平行光束经球面反射镜 M3 成象在 S2 (或 S3)上,进入 S2 后的光 束,经调制器 T 调制成 800Hz 后,再经 M5 反射到深椭球镜 M6 上后成象到接收器 P 的靶面上。 反射镜 M4 是可旋转摆动的,经 M3 反射后的成象光束除可直接投射到 M5 、M6 外,还可以通过 旋转 M4 使反射后的光束成象到 S3上。 2. 接收单元 随着电子技术和电子仪器的高度发展,光辐射测量中多采用对红外辐射敏感的光电器件。本 实验装置采用 PbS 作接收单元,它对波长范围在 800-2500nm 的近红外光有较好的光谱响应。从 单色仪出缝 1 射出的单色光经信号调制器,调制成 800Hz 的频率信号被 PbS 接收

近代物理实验讲义 【实验内容】 1.验证普朗克定律 2。验证斯忒藩一波尔兹曼定律 3.验证维恩位移定律。 4.测量发光体的能量曲线,计算其色温。 【实验步骤】 1.注意:实验时不必调整狭缝的大小。实验过程中出现以下提示时,一律选择“否”。 轻在出厂时已经好了体发村系的由 ,安去对系数正 2.测量黑体辐射曲线。 (1)打开计算机、电控箱及溴钨灯电源,调整溴钨灯电流为1.700A(电流误差控制在0.003A以内), 使按要求调节入射和出射狭缝,预热20分钟。 (2②)以下步骤需根据软件使用说明操作仪器。 (3)扫描1.700A电流对应的黑体辐射曲线(801-2500nm),保存实验数据(最好存为Mt格式) (④)调节溴钨灯电流为1.500,稳定5分钟后,扫描黑体辐射曲线(注意在软件中选择合适的电 流和寄存器)。重复上述步骤,测量1.300A、1.100A、0.900A的黑体辐射曲线并保存数据。 3.实验数据处理 用记事本打开保存的文件(*ft),将得到4列数据,第1列为寄存器编号,第2列为波长, 第4列为实验测量值。删除文件开头部分的说明信息,只保留这4列数据,将文件另存为xt文 本文件。 打开Origin软件,导入实验数据,然后选中数据表第一列,右键,选择严Sort Worksheet/Custom”, 在弹出的对话框中选择A、B两列升序排列,然后按寄存器编号分别将不同寄存器的数据复制到 不同的表格中,并设置波长列为x轴。 将各实验曲线作图,然后用软件的非线性拟合功能(参见附录Ⅱ),用公式(18.1)拟合实验 数据,得到参数T。作T一I曲线,得到溴钨灯色温与电流的关系曲线。 4.验证维恩位移定律。利用0rigi山软件的寻峰插件,得到各实验曲线的峰值波长m,结合前 面得到的色温,验证维恩位移定律
近代物理实验讲义 114 【实验内容】 1. 验证普朗克定律。 2. 验证斯忒藩-波尔兹曼定律。 3. 验证维恩位移定律。 4. 测量发光体的能量曲线,计算其色温。 【实验步骤】 1. 注意: 实验时不必调整狭缝的大小。实验过程中出现以下提示时,一律选择“否”。 2. 测量黑体辐射曲线。 (1) 打开计算机、电控箱及溴钨灯电源,调整溴钨灯电流为 1.700A(电流误差控制在 0.003A 以内), 使按要求调节入射和出射狭缝,预热 20 分钟。 (2) 以下步骤需根据软件使用说明操作仪器。 (3) 扫描 1.700A 电流对应的黑体辐射曲线(801-2500nm),保存实验数据(最好存为 txt 格式)。 (4) 调节溴钨灯电流为 1.500A,稳定 5 分钟后,扫描黑体辐射曲线(注意在软件中选择合适的电 流和寄存器)。重复上述步骤,测量 1.300A、1.100A、0.900A 的黑体辐射曲线并保存数据。 3. 实验数据处理。 用记事本打开保存的文件(*.ftd),将得到 4 列数据,第 1 列为寄存器编号,第 2 列为波长, 第 4 列为实验测量值。删除文件开头部分的说明信息,只保留这 4 列数据,将文件另存为 txt 文 本文件。 打开Origin软件,导入实验数据,然后选中数据表第一列,右键,选择“Sort Worksheet/Custom”, 在弹出的对话框中选择 A、B 两列升序排列,然后按寄存器编号分别将不同寄存器的数据复制到 不同的表格中,并设置波长列为 x 轴。 将各实验曲线作图,然后用软件的非线性拟合功能(参见附录Ⅱ),用公式(18.1)拟合实验 数据,得到参数 T。作 T-I 曲线,得到溴钨灯色温与电流的关系曲线。 4. 验证维恩位移定律。利用 Origin 软件的寻峰插件,得到各实验曲线的峰值波长max,结合前 面得到的色温,验证维恩位移定律