
光学图像微分 实验17光学图像微分 在图像识别技术中,突出图像的边缘是一种重要的方法。人们视觉对于边缘比较敏感,因此 对于一张比较模糊的图像,由于突出了其他边缘轮廓而变得易于识别。为了突出图像的边缘轮院 我们可以用空间滤波的方法,去掉低频而突出高频,从而使图像的轮廓突出。本试验介绍的使利 用光学相关方法作图像的空间微分处理,从而描出图像的轮廓的边缘。 【实验目的】 1.掌握用复合光栅对光学图象进行微分处理的原理和方法 2.初步领会空间滤波的意义,初步了解相干光学处理中常用的的4F系统,加深对光学信总处理 实质的理解 3.通过实验观测对图象微分后突出其边缘轮廓的效果 【实验原理】 光学微分不仅是一种重要的光学一数学运算,在光学图像处理中也是突出信总的一种重要方 法。 在图象识别技术中,突出图象的边缘是一种重要的识别方法。人的视觉对于图象的边缘轮廓 比较敏感,因此对于一张比较模糊的图象,由于突出了其边缘轮完而变得易于辨认。为了突出图 象的边缘轮廓,我们可以用空间滤波的方法,去掉图象中的低领成分而突出图象的高频成分,从 而使轮廊突出。本实验利用光学相关方法作空间的微分处理从而描出图象的边缘,具体的做法是 用复合光栅作为空间滤波器实现图象的微分处理,了解相干光学处理中的4F系统及空间滤波器的 作用。 全息复合光栅法这种方法的基本原理是先使待处理图像生成两个相互有点错位的象,然后通 过改变两个图象的相位让共重叠部分相减而留下由于错位而形成的边沿部分,从而实现图像边缘 增强的效果,从数学角度来说,就是用差分代替了微分。 利用复合光栅进行图像微分的光学系统是典型的4系统,如图17.1所示 入面P1 图17.1相干光学处理系统(4F系统) 一束平行光照射透明物体g(待处理的图像),物体g置于傅氏透镜L的前焦面P处,在L1的后 107
光学图像微分 107 实验17 光学图像微分 在图像识别技术中,突出图像的边缘是一种重要的方法。人们视觉对于边缘比较敏感,因此 对于一张比较模糊的图像,由于突出了其他边缘轮廓而变得易于识别。为了突出图像的边缘轮廓, 我们可以用空间滤波的方法,去掉低频而突出高频,从而使图像的轮廓突出。本试验介绍的使利 用光学相关方法作图像的空间微分处理,从而描出图像的轮廓的边缘。 【实验目的】 1. 掌握用复合光栅对光学图象进行微分处理的原理和方法 2. 初步领会空间滤波的意义,初步了解相干光学处理中常用的的4F系统,加深对光学信息处理 实质的理解 3. 通过实验观测对图象微分后突出其边缘轮廓的效果 【实验原理】 光学微分不仅是一种重要的光学—数学运算,在光学图像处理中也是突出信息的一种重要方 法。 在图象识别技术中,突出图象的边缘是一种重要的识别方法。人的视觉对于图象的边缘轮廓 比较敏感,因此对于一张比较模糊的图象,由于突出了其边缘轮廓而变得易于辨认。为了突出图 象的边缘轮廓,我们可以用空间滤波的方法,去掉图象中的低频成分而突出图象的高频成分,从 而使轮廓突出。本实验利用光学相关方法作空间的微分处理从而描出图象的边缘,具体的做法是 用复合光栅作为空间滤波器实现图象的微分处理,了解相干光学处理中的4F系统及空间滤波器的 作用。 全息复合光栅法这种方法的基本原理是先使待处理图像生成两个相互有点错位的象,然后通 过改变两个图象的相位让其重叠部分相减而留下由于错位而形成的边沿部分,从而实现图像边缘 增强的效果,从数学角度来说,就是用差分代替了微分。 利用复合光栅进行图像微分的光学系统是典型的4f 系统,如图17.1所示: 图 17.1 相干光学处理系统(4F 系统) 一束平行光照射透明物体g(待处理的图像),物体g置于傅氏透镜L1的前焦面P1处,在L1的后

近代物理实验讲义 焦面上得到物函数g(o,o)的频谱G),此频谱面又位于傅氏透镜L2的前焦面上,在1a的后焦面 上得到频谱函数的傅里叶变换。物函数经过两次傅里叶变换又得到了原函数,只是变成了倒像 在图17.1中,P平面采用的x,坐标与P,平面的,为坐标的方向相反,因而可以消除由于两次傅里 叶变换引入的负号。如果在频谱面上插入空间滤波器就可以改变频诣函数,从而使输入信号得到 处理。在本实验中用一个复合光栅作为空间滤波器。下面具体分析复合光橘的空间滤波作用。 1,在P,平面上放置要处理的图像,其振幅透射率为g0,0),用单色平面波垂直照射在图像上, 透过图像后在P面之后的复振幅分布为g如,) 2.透镜L1对g)进行傅里叶变换 (g(xo,o)=G(faf), (17.1) 其中,{)表示对括号里面的函数进行傅立叶变换,人为,坐标系内的空间频率,下同。G, 0是物函数的空间频谱(忽略了常数项),以 :·(F是傅立叶透镜的焦距》 (17.2) 代入G6,月的表达式就得到P平面上的复振幅分布为 ue-号 (17.3) 3.把复合光橱放置在P2平面上,其振幅透射率己知为: 1()=A-cos2mE+cos2π(v+△v)] -A-B(exp(i2mE)+exp(-i2mE) (17.4) +exp[i2a(v+△v)闫+exp[-2z(v+△r)]} 透过复合光栅以后,在P,平面之后的复振幅分布为 U2(e,=U1(e,n)() (17.5) 4.透镜L2对U2(,)又进行傅里叶变换,在P3平面上得到的复振幅分布为 ucn-ue-d是是间-oUu (17.6) 符号*表示卷积,利用傅里叶变换的基本关系式进行一系列运算,我们有: U;(x.y)c Ag(x.y)-B(g(x-vAF.y)+g(x+vAF,y)) (17.7) -Bgx-(v+△v)2F,y+gx+(v+△v)F,y) 把U(x,)和一维正弦光栅的透射光波的复振幅分布 Ux-4-fcas2m-4-号m2m)-号c-2ma) (17.8) 相比较,显然可知:P平面上物频谱受到了两个一维正弦光栅的调制,即其复振幅分布相当 于由两个一维正弦光栅产生。 108
近代物理实验讲义 108 焦面上得到物函数g(x0, y0)的频谱G(fξ, fη),此频谱面又位于傅氏透镜L2的前焦面上,在L2的后焦面 上得到频谱函数的傅里叶变换。物函数经过两次傅里叶变换又得到了原函数,只是变成了倒像。 在图17.1中,P3平面采用的x, y坐标与P1平面的x0, y0坐标的方向相反,因而可以消除由于两次傅里 叶变换引入的负号。如果在频谱面上插入空间滤波器就可以改变频谱函数,从而使输入信号得到 处理。在本实验中用一个复合光栅作为空间滤波器。下面具体分析复合光栅的空间滤波作用。 1. 在 P1 平面上放置要处理的图像,其振幅透射率为 g(x0, y0),用单色平面波垂直照射在图像上, 透过图像后在 P1 面之后的复振幅分布为 g(x0, y0)。 2. 透镜 L1 对 g(x0, y0)进行傅里叶变换 { ( , )} ( , ) 0 0 ξ η g x y = G f f , (17.1) 其中,{ }表示对括号里面的函数进行傅立叶变换,fξ,fη为ξ,η坐标系内的空间频率,下同。G(fξ, fη)是物函数的空间频谱(忽略了常数项),以 , F f λ ξ ξ = F f λ η η = . (F 是傅立叶透镜的焦距) (17.2) 代入G(fξ,fη)的表达式就得到P2平面上的复振幅分布为 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = f F U G λ η λ ξ (ξ,η) , 1 . (17.3) 3. 把复合光栅放置在 P2 平面上,其振幅透射率已知为: exp[ 2 ( ) ] exp[ 2 ( ) ]} {exp( 2 ) exp( 2 ) ( ) [cos2 cos2 ( ) ] π ξ π ξ π ξ π ξ ξ β π ξ π ξ i v v i v v A B i v i v t A v v v + + Δ + − + Δ = − + − = − + + Δ . (17.4) 透过复合光栅以后,在P2平面之后的复振幅分布为 ( , ) ( , ) ( ) U2 ξ η =U1 ξ η t ξ . (17.5) 4. 透镜 L2 对 U2(ξ,η)又进行傅里叶变换,在 P3 平面上得到的复振幅分布为 = ∗ {( ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ( , ) = { ( , )} = , · ( ) { ( , )} ( )} 3 2 ξ ξ λ η λ ξ ξ η ξ η t G f f t F F U x y U G . (17.6) 符号*表示卷积,利用傅里叶变换的基本关系式进行一系列运算,我们有: { [ ( ) , ] [ ( ) , ]} ( , ) ( , ) { ( , ) ( , )} 3 B g x v v F y g x v v F y U x y Ag x y B g x v F y g x v F y λ λ λ λ − − + Δ + + + Δ ∝ − − + + . (17.7) 把U3(x, y)和一维正弦光栅的透射光波的复振幅分布 ( , ) cos 2 exp( 2 ) exp( 2 ) 2 2 U x y A vx A i vx i vx β β = − βπ π π = − − − . (17.8) 相比较,显然可知:P3平面上物频谱受到了两个一维正弦光栅的调制,即其复振幅分布相当 于由两个一维正弦光栅产生
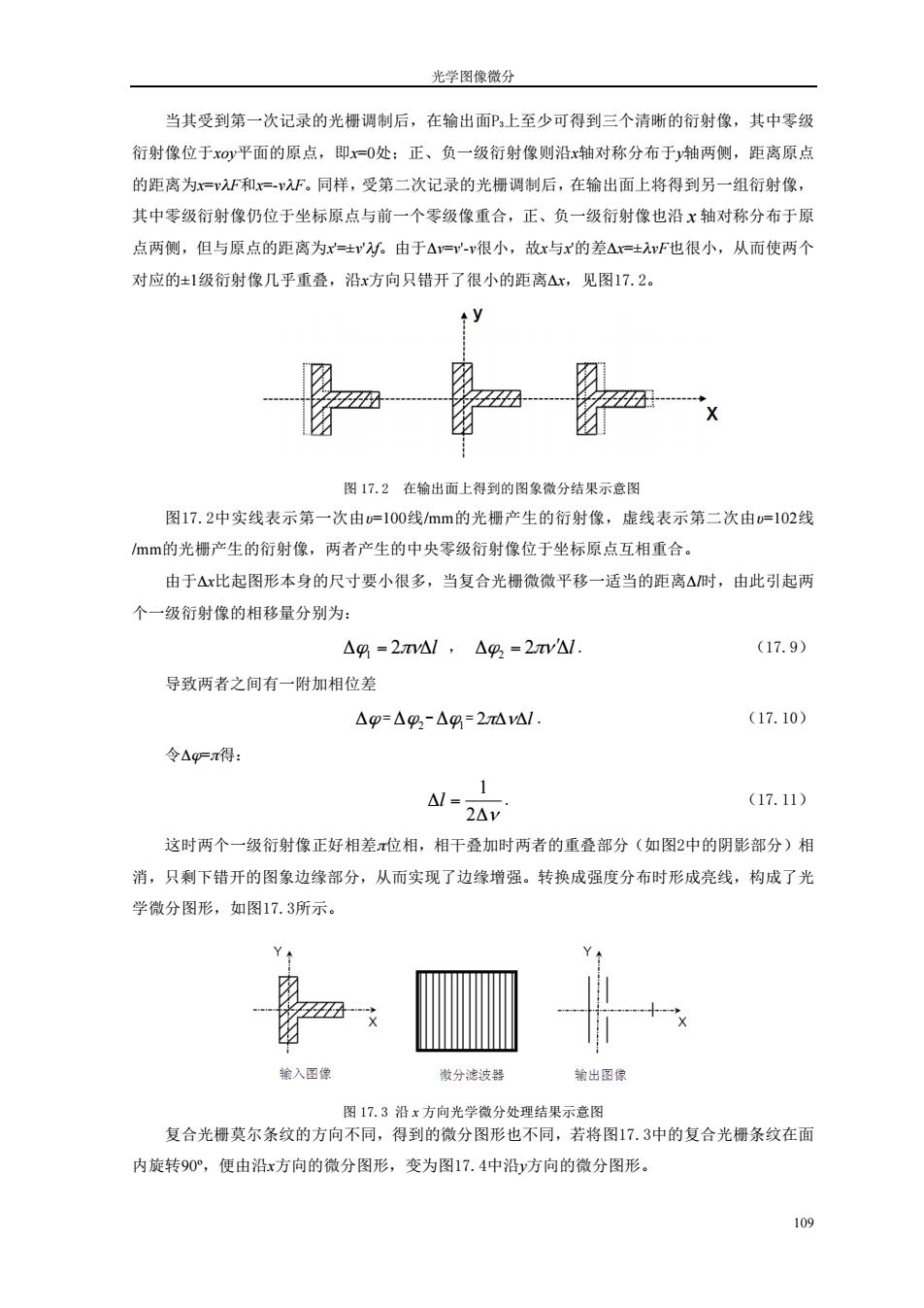
光学图像微分 当其受到第一次记录的光栅调制后,在输出面印,上至少可得到三个清晰的衍射像,其中零级 衍射像位于xO平面的原点,即O处:正、负一级衍射像则沿x轴对称分布于)轴两侧,距离原点 的距离为xF和-入F。同样,受第二次记录的光栅调制后,在输出面上将得到另一组衍射像, 共中零级衍射像仍位于坐标原点与前一个零级像重合,正、负一级衍射像也沿x轴对称分布于原 点两侧,但与原点的距离为r=士水。由于△=v很小,故x与x的差△=±F也很小,从而使两个 对应的±1级衍射像几乎重叠,沿x方向只错开了很小的距离△x,见图17.2。 V 图17.2在给出面上得到的图象微分结果示意图 图17.2中实线表示第一次由=100线mm的光栅产生的衍射像,虚线表示第二次由u=102线 mm的光桶产生的衍射像,两者产生的中央零级衍射像位于坐标原点互相重合。 由于△x比起图形本身的尺寸要小很多,当复合光栅微微平移一适当的距离△时,由此引起两 个一级衍射像的相移量分别为: △%=2,△g=2v (17.9) 导致两者之间有一附加相位差 △p=△94-△4=2d (17.10) 令△g=得: Al-2AV (17.11) 这时两个一级衍射像正好相差π位相,相干叠加时两者的重叠部分(如图2中的阴影部分)相 消,只剩下错开的图象边缘部分,从而实现了边缘增强。转换成强度分布时形成亮线,构成了光 学微分图形,如图17.3所示 嫩分波器 输出图像 图17.3沿x方向光学微分处理结果示意图 复合光棚莫尔条纹的方向不同,得到的微分图形也不同,若将图17.3中的复合光橱条纹在面 内旋转90°,便由沿x方向的微分图形,变为图17.4中沿y方向的微分图形。 109
光学图像微分 109 当其受到第一次记录的光栅调制后,在输出面P3上至少可得到三个清晰的衍射像,其中零级 衍射像位于xoy平面的原点,即x=0处;正、负一级衍射像则沿x轴对称分布于y轴两侧,距离原点 的距离为x=vλF和x=-vλF。同样,受第二次记录的光栅调制后,在输出面上将得到另一组衍射像, 其中零级衍射像仍位于坐标原点与前一个零级像重合,正、负一级衍射像也沿 x 轴对称分布于原 点两侧,但与原点的距离为x'=±v'λf。由于Δv=v'-v很小,故x与x'的差Δx=±λvF也很小,从而使两个 对应的±1级衍射像几乎重叠,沿x方向只错开了很小的距离Δx,见图17.2。 图 17.2 在输出面上得到的图象微分结果示意图 图17.2中实线表示第一次由υ=100线/mm的光栅产生的衍射像,虚线表示第二次由υ=102线 /mm的光栅产生的衍射像,两者产生的中央零级衍射像位于坐标原点互相重合。 由于Δx比起图形本身的尺寸要小很多,当复合光栅微微平移一适当的距离Δl时,由此引起两 个一级衍射像的相移量分别为: 1 Δϕ πν = 2 Δl , 2 Δϕ πν = 2 ʹΔl . (17.9) 导致两者之间有一附加相位差 Δϕ = Δϕ2 - Δϕ1= 2π νΔ Δl . (17.10) 令Δϕ=π得: 1 2 l ν Δ = Δ . (17.11) 这时两个一级衍射像正好相差π位相,相干叠加时两者的重叠部分(如图2中的阴影部分)相 消,只剩下错开的图象边缘部分,从而实现了边缘增强。转换成强度分布时形成亮线,构成了光 学微分图形,如图17.3所示。 图 17.3 沿 x 方向光学微分处理结果示意图 复合光栅莫尔条纹的方向不同,得到的微分图形也不同,若将图17.3中的复合光栅条纹在面 内旋转90º,便由沿x方向的微分图形,变为图17.4中沿y方向的微分图形

近代物理实验讲义 ☑ 输入图像 做分洗波器 输出函惊 图17.4沿y方向光学微分处理结果示意图 【实验内容】 L.利用激光器、扩束镜和准值镜输出平行光,测量扩束镜和准值镜之间的间距和平行光束的直 径,估计激光束的直径, 2.用‘S'形物体和两个傅立叶透镜,在光屏上得到倒立、等大、清晰的实像 3.利用微分滤波器(复合光栅),观察微分图像。 4.改变微分滤波器的条纹方向,观察微分图像的变化。 【实验步骤】 本实验采用=100线mm,w=02线mm组成的复合光橱,其莫尔条纹须率△u=2线mm。拍摄 光学微分图像实验的实际光路如图17.5所示,这是典型的4F相干光学处理系统。 微分滤液器 激光器 叶频 镜面 图17.5实验光路原理图 光路可按如下步骤调节: 1.搭光路,利用反射镜、扩束镜、准直镜产生方向符合需要的平行光。 2.在平行光東前面先放上透镜L及屏P2,移动P2的位置使平行光束经过L聚焦在P2面上, 则P2位于L1的后焦面上,这就是频谐面。固定L1及P2的底座。 3.在L1左边距离为F的P1面处放上要处理的图像(S形图案),拿走屏P2,放上透镜2及屏 P:,移动P,使在屏上看到物的等大、倒立、清断的像。 调节时可在透明图片前放上毛玻璃,使得成像的景深较短,便于确定清晰成像的位置。,及 P的位置确定之后,固定L及P的底座,撤去毛玻璃。 4.在P2面上放上复合光栅,用一维水平可调底座沿垂直于光轴的水平方向平移复合光栅,从屏 P上观察图像的变化,找到最好的微分图像,然后固定住复合光栅底座。 110
近代物理实验讲义 110 图 17.4 沿 y 方向光学微分处理结果示意图 【实验内容】 1. 利用激光器、扩束镜和准值镜输出平行光,测量扩束镜和准值镜之间的间距和平行光束的直 径,估计激光束的直径。 2. 用‘S’形物体和两个傅立叶透镜,在光屏上得到倒立、等大、清晰的实像。 3. 利用微分滤波器(复合光栅),观察微分图像。 4. 改变微分滤波器的条纹方向,观察微分图像的变化。 【实验步骤】 本实验采用υ=100线/mm,υ0=102线/mm组成的复合光栅,其莫尔条纹频率Δυ=2线/mm。拍摄 光学微分图像实验的实际光路如图17.5所示,这是典型的4F相干光学处理系统。 图17.5 实验光路原理图 光路可按如下步骤调节: 1. 搭光路,利用反射镜、扩束镜、准直镜产生方向符合需要的平行光。 2. 在平行光束前面先放上透镜 L1 及屏 P2,移动 P2 的位置使平行光束经过 L1 聚焦在 P2 面上, 则 P2 位于 L1 的后焦面上,这就是频谱面。固定 L1 及 P2 的底座。 3. 在 L1 左边距离为 F1 的 P1 面处放上要处理的图像(‘S’形图案),拿走屏 P2,放上透镜 L2 及屏 P3,移动 P3 使在屏上看到物的等大、倒立、清晰的像。 调节时可在透明图片前放上毛玻璃,使得成像的景深较短,便于确定清晰成像的位置。L2及 P3的位置确定之后,固定L2及P3的底座,撤去毛玻璃。 4. 在 P2 面上放上复合光栅,用一维水平可调底座沿垂直于光轴的水平方向平移复合光栅,从屏 P3 上观察图像的变化,找到最好的微分图像,然后固定住复合光栅底座