
实验4.9用非线性电路研究混沌现象 非线性科学和复杂系统的研究是21世纪科学研究的一个重要方向。非线性科学的 研究对了解生物、物理、化学、气象等学科都有重要意义。最近20多年,混沌作为非线性 科学中的主要研究对象之一,在许多领域都得到了证实和应用。混沌作为一门新学科,填 补着自然界决定论和概率论的鸿沟。混沌是对经典决定论的否定,但其本身有它特有的 规律。研究混沌的目的是要揭示貌似随机的现象背后所隐藏的规律。 混沌运动最主要的特征是具有初值敏感性和长时间发展趋势的不可预见性。混沌研 究表明,一个完全确定的系统,即使非常简单,由于系统内部的非线性作用,同样具有内在 的随机性,可以产生随机性的非周期运动一混沌。在许多非线性动力学系统中,既有周 期运动,又有混沌运动。混沌运动是非线性方程所特有的一种解,不是由外噪声引起的, 混沌吸引子是由确定性方程中非线性因素直接得到的具有随机性运动的一种状态。本实 验通过一个简单的电路产生混沌,观察倍周期分叉产生混沌的过程,同时了解非线性电阻 对产生混沌的作用,了解混沌现象的一些基本特征。 【实验目的 1.通过对非线性电路的分析,了解产生混沌现象的基本条件: 2.通过调整Chua电路的参数,学习倍周期分叉走向混沌的过程: 3.在示波器上观察混沌的各种相图:单吸引子和双吸引子: 4.测量电路中非线性电阻的1U特性。 【实验原理 混沌产生的必要条件是系统具有非线性因素。图4.9.1()是讨论非线性电路系统 的一种简单的电路Cua电路。电路中一共只需要5个基本电路元件4个线性元件 L、C、R、C和一个非线性元件R。电路中电感L和电容C并联构成一个LC振荡电 路。可变电阻R的作用是把振荡信号耦合到非线性电阻R上。理想的非线性元件R是 一个分段线性的电阻,它的伏安特性如图4.91b)所示。 根据电路原理图4.9.1()可建立如下方程组: cg-t&-uwY (4.9.1) (49.2) 176
实验4 .9 用非线性电路研究混沌现象 非线性科学和复杂系统的研究是21 世纪科学研究的一个重要方向。非线性科学的 研究对了解生物、物理、化学、气象等学科都有重要意义。最近20 多年, 混沌作为非线性 科学中的主要研究对象之一, 在许多领域都得到了证实和应用。混沌作为一门新学科, 填 补着自然界决定论和概率论的鸿沟。混沌是对经典决定论的否定, 但其本身有它特有的 规律。研究混沌的目的是要揭示貌似随机的现象背后所隐藏的规律。 混沌运动最主要的特征是具有初值敏感性和长时间发展趋势的不可预见性。混沌研 究表明, 一个完全确定的系统, 即使非常简单, 由于系统内部的非线性作用, 同样具有内在 的随机性, 可以产生随机性的非周期运动———混沌。在许多非线性动力学系统中, 既有周 期运动, 又有混沌运动。混沌运动是非线性方程所特有的一种解, 不是由外噪声引起的; 混沌吸引子是由确定性方程中非线性因素直接得到的具有随机性运动的一种状态。本实 验通过一个简单的电路产生混沌, 观察倍周期分叉产生混沌的过程, 同时了解非线性电阻 对产生混沌的作用, 了解混沌现象的一些基本特征。 [ ᇔ僂ⴤⲺ] 1 . 通过对非线性电路的分析, 了解产生混沌现象的基本条件; 2 . 通过调整Chua 电路的参数, 学习倍周期分叉走向混沌的过程; 3 . 在示波器上观察混沌的各种相图: 单吸引子和双吸引子; 4 . 测量电路中非线性电阻的I- U 特性。 [ ᇔ僂⨼] 混沌产生的必要条件是系统具有非线性因素。图4 .9 .1( a) 是讨论非线性电路系统 的一种简单的电路———Chua 电路。电路中一共只需要5 个基本电路元件:4 个线性元件 L 、C1 、R0 、C2 和一个非线性元件 R。电路中电感 L 和电容 C2 并联构成一个 LC 振荡电 路。可变电阻 R0 的作用是把振荡信号耦合到非线性电阻 R 上。理想的非线性元件 R 是 一个分段线性的电阻, 它的伏安特性如图4 .9 .1( b) 所示。 根据电路原理图4 .9 .1( a) 可建立如下方程组: C1 dUC 1 dτ= 1 R0 ( UC 2 - UC 1 ) - f ^( UC 1 ) ( 4 .9 .1) C2 dUC 2 dτ= 1 R0 ( UC1 - UC2 ) + i L ( 4 .9 .2) 176
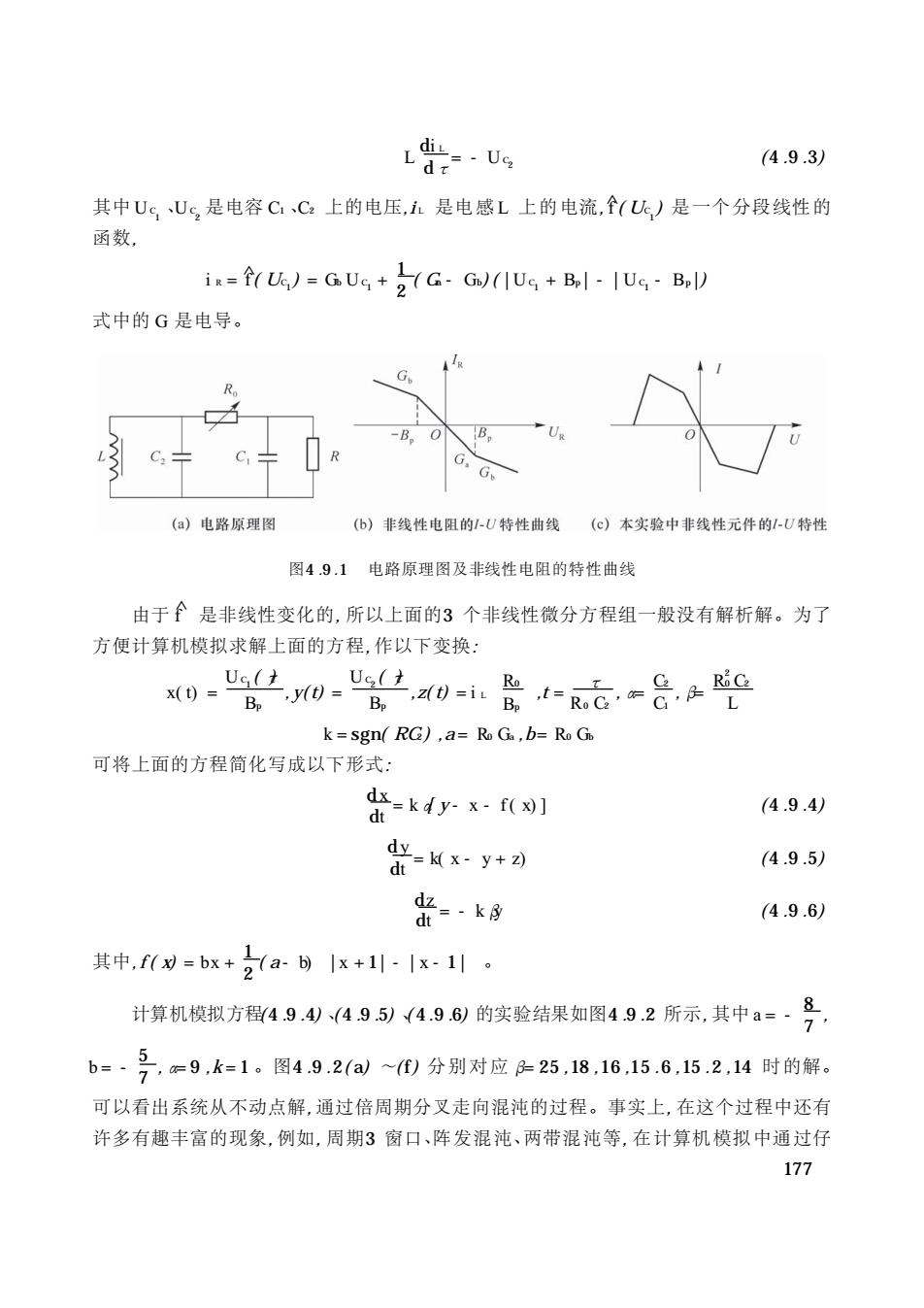
L-.Us 4.9.3) 其中UsUs,是电容CC上的电压,1是电感L上的电流,个(U)是一个分段线性的 函数, i=fU)=GUe+2(G-G)(Us+Bl-IUs-B) 式中的G是电导。 (a)电路原理图 (b)非线性电阻的-U特性曲线(©)本实验中非线性元件的1-U特性 图4.91电路原理图及非线性电阻的特性曲线 由于金是非线性变化的,所以上面的3个非线性微分方程组一般没有解析解。为了 方便计算机模拟求解上面的方程,作以下变换: Ue( x()= k=sgn(RG),a=Ro G.,b=Ro G 可将上面的方程简化写成以下形式: -ky0对] (4.9.4) 出-y+习 (4.9.5) 0-k (4.9.6) 其中,f父=bx+2(a-b)1x+1-Ix-1川。 计算机模拟方留49.4山495)(4.96)的实验结果如图49.2所示,其中a=·号 b=-5,=9,k=1。图4.9.2a~)分别对应25,18,16,15.6,152,14时的解。 可以看出系统从不动点解,通过倍周期分叉走向混沌的过程。事实上,在这个过程中还有 许多有趣丰富的现象,例如,周期3窗口、阵发混沌、两带混沌等,在计算机模拟中通过仔 177
L di L dτ= - UC 2 ( 4 .9 .3) 其中 UC 1 、UC 2 是电容 C1 、C2 上的电压,i L 是电感 L 上的电流,^f ( UC 1 ) 是一个分段线性的 函数, i R = ^f( UC1 ) = Gb UC1 + 1 2 ( Ga - Gb) ( |UC1 + Bp|- |UC1 - Bp|) 式中的 G 是电导。 图4 .9 .1 电路原理图及非线性电阻的特性曲线 由于 f ^ 是非线性变化的, 所以上面的3 个非线性微分方程组一般没有解析解。为了 方便计算机模拟求解上面的方程, 作以下变换: x( t) = UC 1 ( τ) Bp , y( t) = UC 2 ( τ) Bp ,z( t) = i L R0 Bp ,t = τ R0 C2 ,α= C2 C1 ,β= R2 0 C2 L k = sgn( RC2 ) ,a= R0 Ga ,b= R0 Gb 可将上面的方程简化写成以下形式: dx dt = kα[ y - x - f ( x) ] ( 4 .9 .4) dy dt = k( x - y + z) ( 4 .9 .5) dz dt = - kβy ( 4 .9 .6) 其中, f ( x) = bx + 1 2 ( a- b) |x + 1| - |x - 1| 。 计算机模拟方程( 4 .9 .4) 、( 4 .9 .5) 、( 4 .9 .6) 的实验结果如图4 .9 .2 所示, 其中 a = - 8 7 , b= - 5 7 ,α= 9 ,k = 1 。图4 .9 .2( a) ~( f) 分别对应β= 25 ,18 ,16 ,15 .6 ,15 .2 ,14 时的解。 可以看出系统从不动点解, 通过倍周期分叉走向混沌的过程。事实上, 在这个过程中还有 许多有趣丰富的现象, 例如, 周期3 窗口、阵发混沌、两带混沌等, 在计算机模拟中通过仔 177
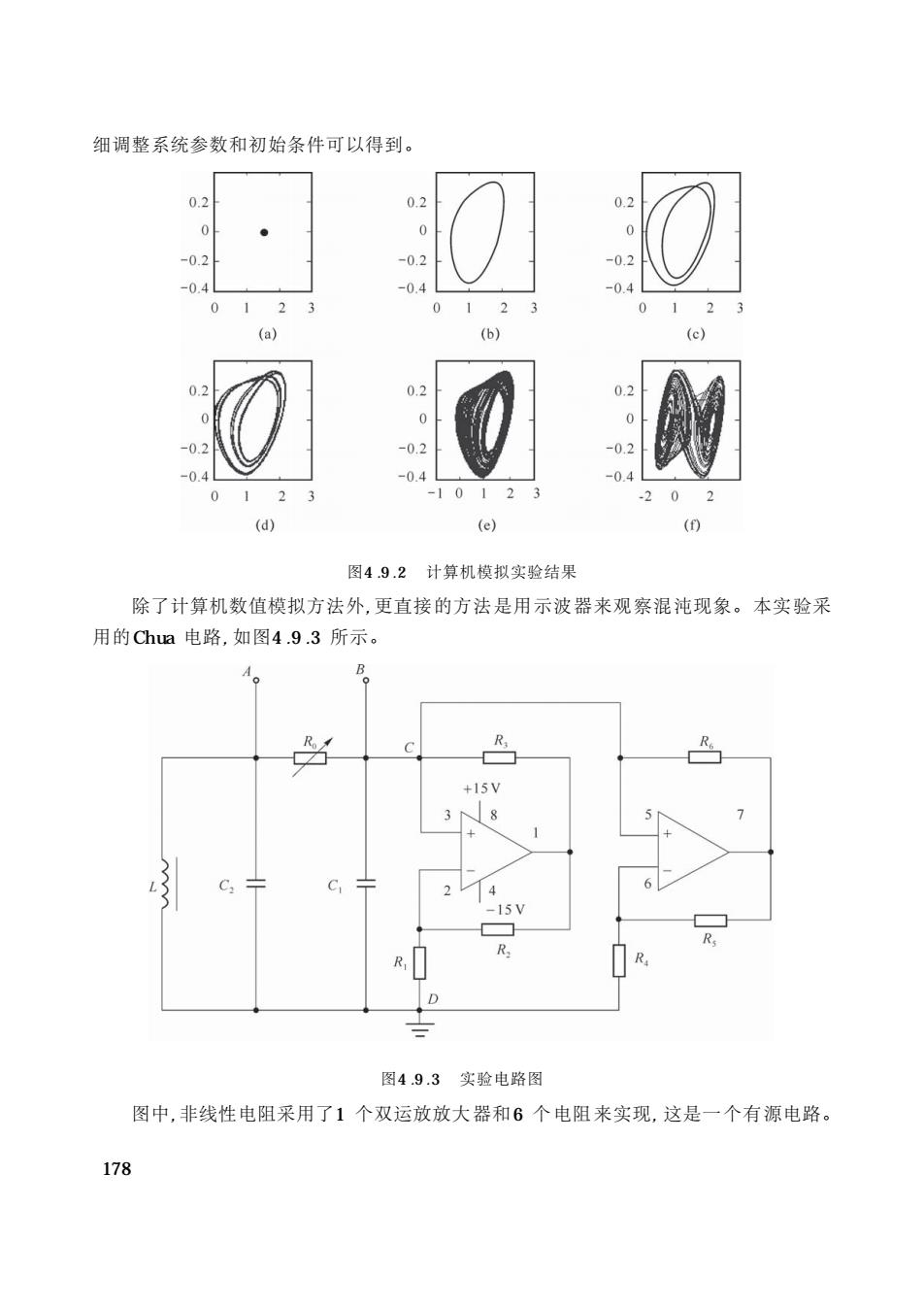
细调整系统参数和初始条件可以得到。 0.2 0.2 0.2 -0.4 04 (a】 (6) (c) -0. -04 -1012 (d) (e) (0 图49.2计算机模拟实验结果 除了计算机数值模拟方法外,更直接的方法是用示波器来观察混沌现象。本实验采 用的Chua电路,如图4.9.3所示。 +15V C 图4.9.3实验电路图 图中,非线性电阻采用了1个双运放放大器和6个电阻来实现,这是一个有源电路。 178
细调整系统参数和初始条件可以得到。 图4 .9 .2 计算机模拟实验结果 除了计算机数值模拟方法外, 更直接的方法是用示波器来观察混沌现象。本实验采 用的Chua 电路, 如图4 .9 .3 所示。 图4 .9 .3 实验电路图 图中, 非线性电阻采用了1 个双运放放大器和6 个电阻来实现, 这是一个有源电路。 178

双运放器件TL082的前级和后级的正负反馈同时存在,正反馈的强弱与比值R/、R/R 有关,负反馈的强弱与比值R/R/有关。当正反馈大于负反馈时,LG电路才能产 生并维持振荡。若调节R,正反馈强度的变化可以改变LC的振荡情况,出现周期振荡 倍周期分叉和混沌等现象。由于双运放器件TL082的非线性作用,从C、D两点看】 TL082与6个电阻的组合等效于一个非线性电阻,它的伏安特性大致如图4.9.1(c)所 示,所以说Ca电路实际上是一个可调的特殊振荡器。 在本实验中,用示波器观察电容C和C上的电压信号,即在示波器上显示U,U 的合成图形,通过改变R和电感L的值观察混沌现象。 图中的元件参考值为:L=18mH,G=10nF,G=100nF,R-3.3kQ,=Rs= 22k2,R=2.2k9,R=R=220Q。R由2.2kQ与100Q的两个多圈电位器串联组 成,因此可以粗调和细调。 【实验仪器 非线性电路与混沌实验仪,示波器,电阻箱,数字万用表。 【实验内阁 1.倍周期现象、周期窗口、单吸引子和双吸引子的观察、记录和描述 (1)将电容C,和C上的电压信号输入到示波器的xy轴,示波器屏上一般可观察 到不稳定的曲线,略微调节R。,即能迅速稳定。调节R,可见曲线作倍周期变化,曲线由 1周期倍增至2周期,由2周期倍增至4周期,… (2)继续调节R,通过多次倍周期分叉,会出现一个难以计数的闭合的环状曲线.这 是一个单涡旋吸引子集。再细微调节,单吸引子突然变成双吸引子,而且两个吸引子 基本上是对称的。双吸引子的相图在混沌研究的文献中又称为蝴蝶现象,这也是一种 奇怪吸引子,它们的特点是整体上的稳定性和局域上的不稳定性同时存在。如果在某一 时刻加上一个小的噪声或其他微小变化,它的运动轨迹与原来不加干扰的轨迹相比会发 生很大的变化,其差异随时间的增加是按指数规律变化的。这就是混沌现象的初值敏感 性特征。由于混沌是系统中多个周期轨道的不稳定而产生的,如果仔细调整R,还可观 察3周期轨道和阵发混沌现象。阵发混沌是混沌与周期无规律地交替出现的现象。 (3)在Chua电路中,调节电感L也可以使吸引子发生变化.仔细调节电感L的磁芯 改变L的大小,观察上面出现的现象。 (4)用坐标纸按1:1的比例画出各种周期的曲线,并记录以上现象的特点。 2.测量电路中等效非线性电阻的伏安特性曲线 (1)取下电感L,将图4.9.3中的C、D两点作为输出端,外接电流表和一个电阻箱 「。由于这里的非线性电阻是有源的,因此回路中始终有电流。r的作用是改变非线性元 179
双运放器件 TL082 的前级和后级的正负反馈同时存在, 正反馈的强弱与比值 R3/ R0 、R6/ R0 有关, 负反馈的强弱与比值 R2/ R1 、R5/R4 有关。当正反馈大于负反馈时, LC1 电路才能产 生并维持振荡。若调节 R0 , 正反馈强度的变化可以改变 LC1 的振荡情况, 出现周期振荡、 倍周期分叉和混沌等现象。由于双运放器件 TL082 的非线性作用, 从 C、D 两点看, TL082 与6 个电阻的组合等效于一个非线性电阻, 它的伏安特性大致如图4 .9 .1( c) 所 示, 所以说 Chua 电路实际上是一个可调的特殊振荡器。 在本实验中, 用示波器观察电容 C1 和 C2 上的电压信号, 即在示波器上显示 UC1 、UC 2 的合成图形, 通过改变 R0 和电感 L 的值观察混沌现象。 图中的元件参考值为: L= 18 mH, C1 = 10 nF , C2 = 100 nF , R1 = 3 .3 kΩ, R2 = R3 = 22 kΩ, R4 = 2 .2 kΩ, R5 = R6 = 220 Ω。R0 由2 .2 kΩ 与100 Ω的两个多圈电位器串联组 成, 因此可以粗调和细调。 [ ᇔ僂Ԡಞ] 非线性电路与混沌实验仪, 示波器, 电阻箱, 数字万用表。 [ ᇔ僂ᇯ] 1 . كઞᵕ⧦䊗ȽઞᵕネਙȽঋ੮ᕋᆆૂਂ੮ᕋᆆⲺ㿸ሕȽ䇦ᖋૂᨅ䘦 ( 1) 将电容 C1 和 C2 上的电压信号输入到示波器的 x 、y 轴, 示波器屏上一般可观察 到不稳定的曲线, 略微调节 R0 , 即能迅速稳定。调节 R0 , 可见曲线作倍周期变化, 曲线由 1 周期倍增至2 周期, 由2 周期倍增至4 周期, …… ( 2) 继续调节 R0 , 通过多次倍周期分叉, 会出现一个难以计数的闭合的环状曲线, 这 是一个单涡旋吸引子集。再细微调节 R0 , 单吸引子突然变成双吸引子, 而且两个吸引子 基本上是对称的。双吸引子的相图在混沌研究的文献中又称为“蝴蝶”现象, 这也是一种 奇怪吸引子, 它们的特点是整体上的稳定性和局域上的不稳定性同时存在。如果在某一 时刻加上一个小的噪声或其他微小变化, 它的运动轨迹与原来不加干扰的轨迹相比会发 生很大的变化, 其差异随时间的增加是按指数规律变化的。这就是混沌现象的初值敏感 性特征。由于混沌是系统中多个周期轨道的不稳定而产生的, 如果仔细调整 R0 , 还可观 察3 周期轨道和阵发混沌现象。阵发混沌是混沌与周期无规律地交替出现的现象。 ( 3) 在 Chua 电路中, 调节电感 L 也可以使吸引子发生变化, 仔细调节电感 L 的磁芯 改变L 的大小, 观察上面出现的现象。 ( 4) 用坐标纸按1 ∶1 的比例画出各种周期的曲线, 并记录以上现象的特点。 2 . ⎁䠅⭫䐥ѣㅿ᭾䶔㓵ᙝ⭫䱱ⲺՅᆿ⢯ᙝᴨ㓵 ( 1) 取下电感 L , 将图4 .9 .3 中的 C、D 两点作为输出端, 外接电流表和一个电阻箱 r 。由于这里的非线性电阻是有源的, 因此回路中始终有电流。r 的作用是改变非线性元 179

件的对外输出,虽然所用的电阻箱改变的电阻不连续,但并不影响本实验的测量。测量的 伏安特性曲线就是改变得到的不同电压下非线性电阻的变化规律。 (2)将电压表读数从-0.1V一直调到-12V左右,尽量多测数据点。 (3)对以上数据作图,并对3段进行线性拟合,分别求出它们的斜率。对于正向电压 部分的曲线,由理论分析和计算得知是与反向电压部分曲线关于原点呈180°对称的。 [思考题 1.混沌现象的产生条件是什么?实验中为什么用相图来观测倍周期分叉等现象? 2.通过本实验阐述一下倍周期分叉、混沌、奇怪吸引子等概念的物理意义。 3.如何理解混沌是确定系统的随机性行为”?在实验中如何观察混沌的初值敏感 性的特点? 180
件的对外输出, 虽然所用的电阻箱改变的电阻不连续, 但并不影响本实验的测量。测量的 伏安特性曲线就是改变r 得到的不同电压下非线性电阻的变化规律。 ( 2) 将电压表读数从- 0 .1 V 一直调到- 12 V 左右, 尽量多测数据点。 ( 3) 对以上数据作图, 并对3 段进行线性拟合, 分别求出它们的斜率。对于正向电压 部分的曲线, 由理论分析和计算得知是与反向电压部分曲线关于原点呈180°对称的。 [ ᙓ㘹从] 1 . 混沌现象的产生条件是什么? 实验中为什么用相图来观测倍周期分叉等现象? 2 . 通过本实验阐述一下倍周期分叉、混沌、奇怪吸引子等概念的物理意义。 3 . 如何理解“混沌是确定系统的随机性行为”? 在实验中如何观察混沌的初值敏感 性的特点? 180