
2v9 电磁场与电磁波基础 主讲:徐乐 商安花子作技大是
电磁场与电磁波基础 主讲:徐乐
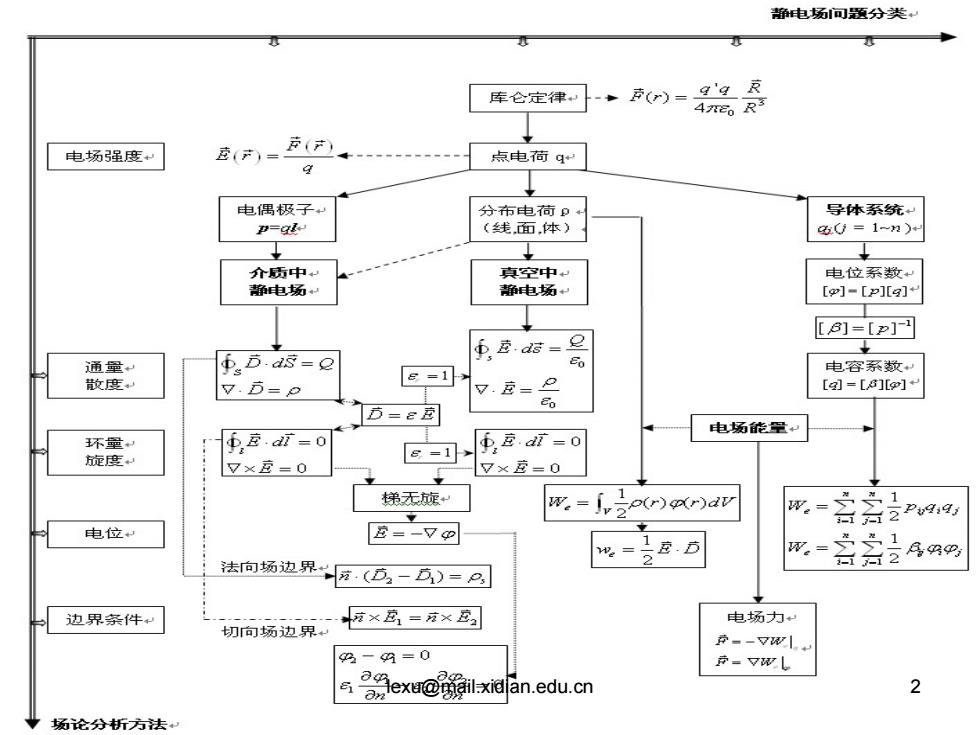
静电场可题分类 库仓定律和 +()=9'g哀 4%R 电场强度 龙()=(产 点电荷q 电偶极子 分布电荷p 导体系统 卫=及 (线面本) 0=1n)+ 介质中 真空中和 电位系数 静电场 静电场 [g]-[P][a] ]=[P]可 币应d塔=旦 通量 .B.ds-e 电容系数 散度 v.方=P E=可入 v.克=2 [g]=[B][]9 D=e园 电场能量 不量 f克.f=o 玉克i=0 旋度 7×应=0 g团> 7×应=0 梯无旋 w,-f,d 电位和 E=-72 =BD W。= 1 法向场边界方(D2-D)=只 五六之8吗吗 边界条件 惊×高=克× 电场力“ 切向场边界 京--W引 一=0 南=V说L exu@喻lx间in.edu.cn 69 2 场论分析方法
lexu@mail.xidian.edu.cn 2

第5讲恒定电流的电场 电流与电荷 一电流密度 一电荷守恒定律 -欧姆定律 一焦耳定律 恒定电流的电场 一基本方程 一边界条件 ·静电比拟法 lexu@mail.xidian.edu.cn 3
第5讲 恒定电流的电场 • 电流与电荷 – 电流密度 – 电荷守恒定律 – 欧姆定律 – 焦耳定律 • 恒定电流的电场 – 基本方程 – 边界条件 • 静电比拟法 lexu@mail.xidian.edu.cn 3

电流密度 ·在电磁理论中主要研究两类电流: 一导体中自由电荷在电场作用下的定向运动形成的电流一传导 电流 一带电粒子在真空中或气体中运动时形成的电流一运流电流 ·密度为ρ的带电粒子以速度v运动时运流电流密度为: J=pv lexu@mail.xidian.edu.cn
电流密度 • 在电磁理论中主要研究两类电流: – 导体中自由电荷在电场作用下的定向运动形成的电流—传导 电流 – 带电粒子在真空中或气体中运动时形成的电流—运流电流 • 密度为ρ的带电粒子以速度v运动时运流电流密度为: J v = ρ lexu@mail.xidian.edu.cn 4

电流密度 。 导体内自由电子在外加电场的作用下会沿着与电场相反的方向运 动,电流就是电荷运动形成的电荷流。 ·不随时间变化的电流称为恒定电流。 ·要在导体中维持恒定电流,其内部必须有恒定的电场,同时恒定 电流又要在其周围空间激发磁场。 ·恒定电流的电场和磁场都不随时间变化,它们彼此独立,互不影 响,因为可以分别加以研究。 lexu@mail.xidian.edu.cn 5
电流密度 • 导体内自由电子在外加电场的作用下会沿着与电场相反的方向运 动,电流就是电荷运动形成的电荷流。 • 不随时间变化的电流称为恒定电流。 • 要在导体中维持恒定电流,其内部必须有恒定的电场,同时恒定 电流又要在其周围空间激发磁场。 • 恒定电流的电场和磁场都不随时间变化,它们彼此独立,互不影 响,因为可以分别加以研究。 lexu@mail.xidian.edu.cn 5

电流密度 在导体中取一截面S,若在时间△t内流过该截面的总电荷为△q, 则通过该截面的电流强度定义为: I=lim Ag=dq △-0△tdt 一电流强度通常简称为电流,单位:安培(A) 一当导线横向尺寸可忽略时,电流称为线电流,对于线电流用 电流强度来描述就足够了。 一当导体的横向尺寸不能忽略时,应该认为电流分布在整个导 体的截面上,这种电流称为体电流: 一如果电流在一个厚度可忽略的导体曲面上流动,则称之为面 电流。 lexu@mail.xidian.edu.cn 6
电流密度 • 在导体中取一截面S,若在时间△t内流过该截面的总电荷为△q, 则通过该截面的电流强度定义为: – 电流强度通常简称为电流,单位:安培(A) – 当导线横向尺寸可忽略时,电流称为线电流,对于线电流用 电流强度来描述就足够了。 – 当导体的横向尺寸不能忽略时,应该认为电流分布在整个导 体的截面上,这种电流称为体电流; – 如果电流在一个厚度可忽略的导体曲面上流动,则称之为面 电流。 dt d q t q I t = ∆ ∆ = ∆ →0 lim lexu@mail.xidian.edu.cn 6
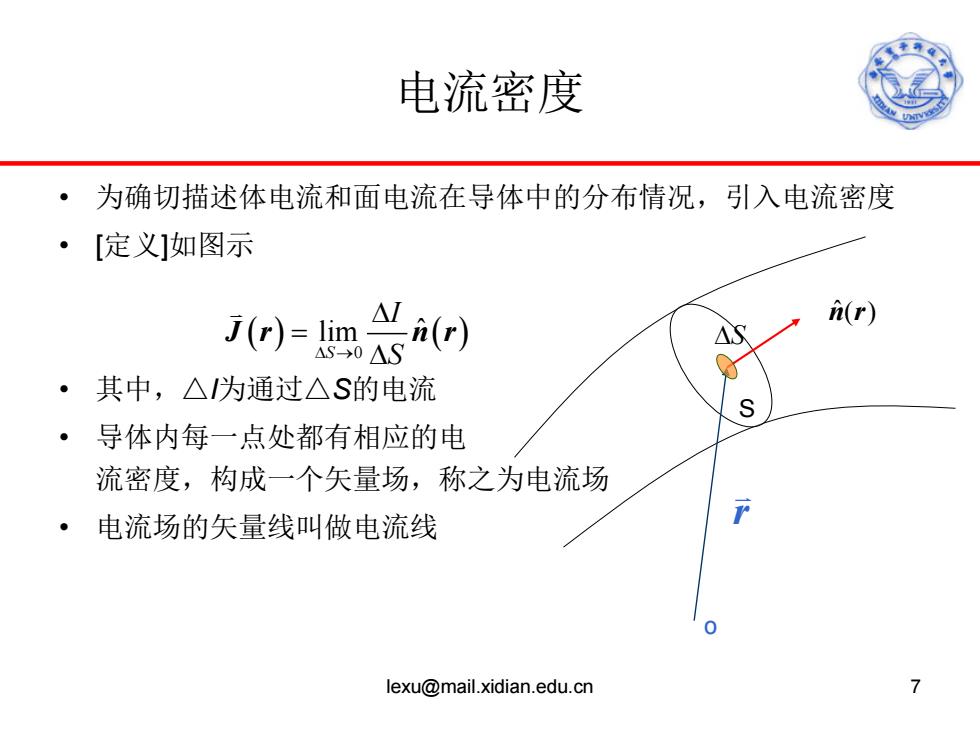
电流密度 ·为确切描述体电流和面电流在导体中的分布情况,引入电流密度 ·[定义]如图示 △ J(r)=lim i(r) (r) △S △S-0△S ·其中,△为通过△S的电流 S ·导体内每一点处都有相应的电 流密度,构成一个矢量场,称之为电流场 ·电流场的矢量线叫做电流线 lexu@mail.xidian.edu.cn >
电流密度 • 为确切描述体电流和面电流在导体中的分布情况,引入电流密度 • [定义]如图示 • 其中,△I为通过△S的电流 • 导体内每一点处都有相应的电 流密度,构成一个矢量场,称之为电流场 • 电流场的矢量线叫做电流线 S n r ˆ( ) r o ( ) ( ) ∆S 0 lim ˆ S I ∆ → S ∆ = ∆ Jr nr lexu@mail.xidian.edu.cn 7

电流密度 ·流过截面的电流就是J对S的通量 1=1 j.ds ·对于面电流,则定义 Js(F)=lim ALi() △1-→0△1 ·通过任意曲线的面电流为: 41 n(r) 1,=∫1J,×d1 lexu@mail.xidian.edu.cn 8
电流密度 • 流过截面的电流就是J对S的通量 • 对于面电流,则定义 • 通过任意曲线l的面电流为: ∫ = ⋅ S I J dS ( ) n (r) l I J r l S ∆ ∆ = ∆ →0 lim | | s s l I J dl = × ∫ lexu@mail.xidian.edu.cn 8
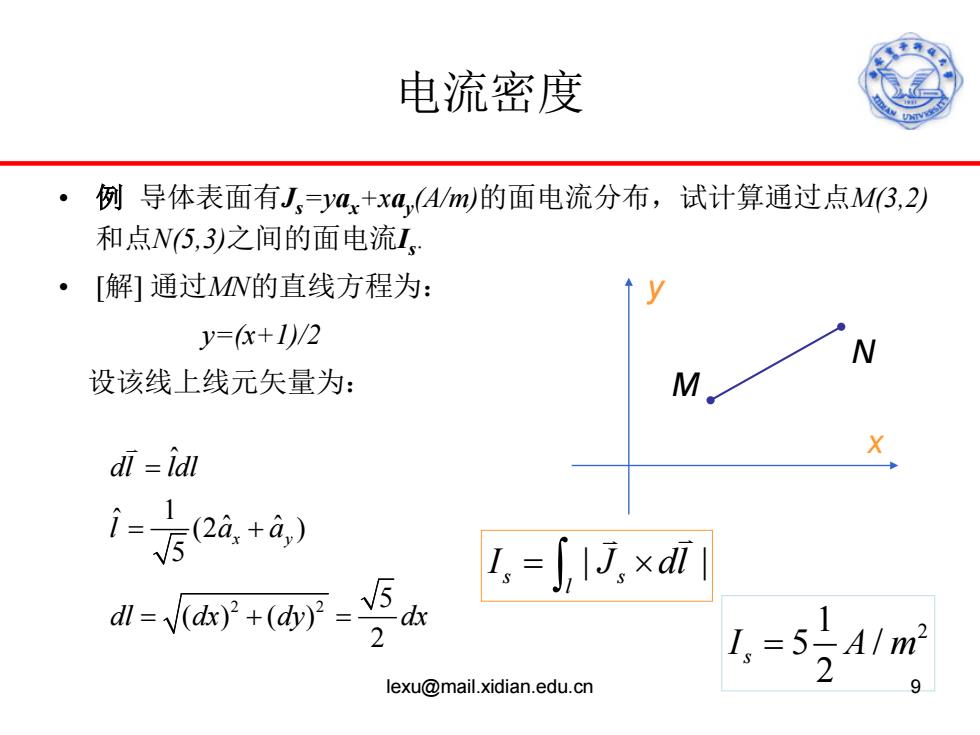
电流密度 ·例导体表面有J,=ya+xa,A/m的面电流分布,试计算通过点M(3,2) 和点N5,3)之间的面电流L ·[解]通过MW的直线方程为: y=(x+1)/2 N 设该线上线元矢量为: M X dl idl 1=1 52a,+a,) 1,=∫1J,×ai d-Ndx)+(avy-dx 1=5A/m2 2 lexu@mail.xidian.edu.cn
电流密度 • 例 导体表面有Js=yax+xay(A/m)的面电流分布,试计算通过点M(3,2) 和点N(5,3)之间的面电流Is. • [解] 通过MN的直线方程为: y=(x+1)/2 设该线上线元矢量为: M N x y 2 2 ˆ 1 ˆ (2 ) ˆ ˆ 5 5 () () 2 x y dl ldl l aa dl dx dy dx = = + = += | | s s l I J dl = × ∫ 1 2 5 / 2 s I Am = lexu@mail.xidian.edu.cn 9
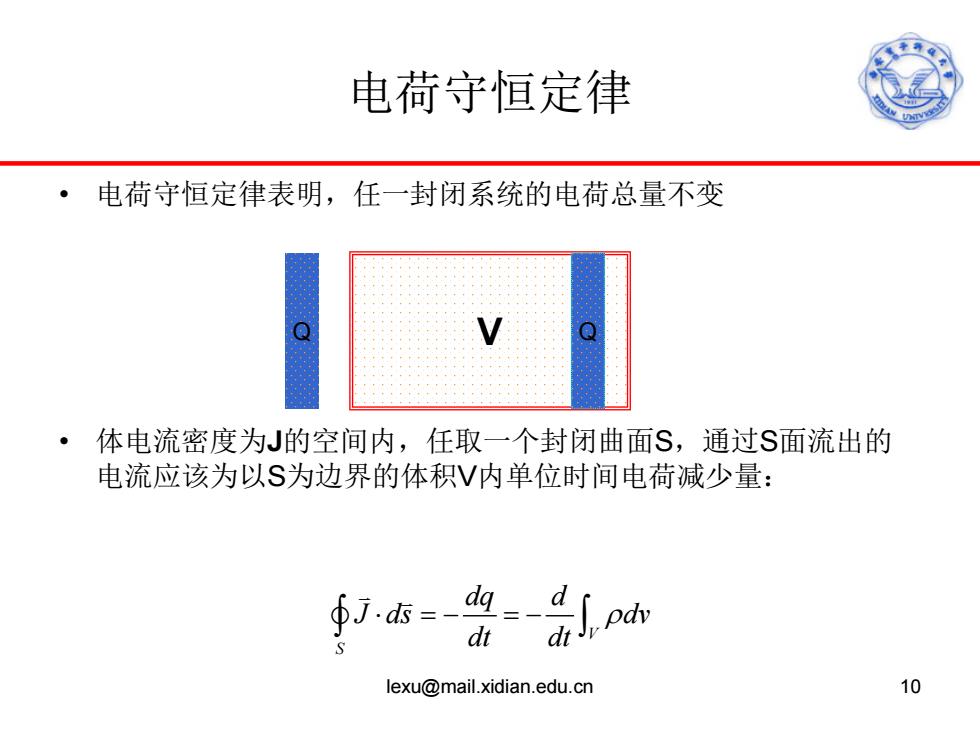
电荷守恒定律 ·电荷守恒定律表明,任一封闭系统的电荷总量不变 ·体电流密度为J的空间内,任取一个封闭曲面S,通过S面流出的 电流应该为以S为边界的体积V内单位时间电荷减少量: ∮75=-9 lexu@mail.xidian.edu.cn 10
电荷守恒定律 • 电荷守恒定律表明,任一封闭系统的电荷总量不变 • 体电流密度为J的空间内,任取一个封闭曲面S,通过S面流出的 电流应该为以S为边界的体积V内单位时间电荷减少量: Q V Q V S dq d J ds dv dt dt ⋅ =− =− ρ ∫ ∫ lexu@mail.xidian.edu.cn 10