
Review 时变电磁场的边界条件 n×(E2-E)=0 n:(B2-B)=0 n×(i2-i)=Js +(J2n=Jin)=- ops 8t (D,-D)=Ps 。时变电磁场的能量 (xd-av+1JEav F=:F)-nx(nxF)=En+Fi V×A=F台(V,×An+Vn×A),+(V,×A)n=E+Fn lexu@mail.xidian.edu.cn
Review 时变电磁场的边界条件 时变电磁场的能量 lexu@mail.xidian.edu.cn 2 ˆˆˆˆˆ () ( ) ˆ F n n F n n F F n Ft = ⋅ −× × = + n t ( )( ) ∇× = ⇔ ∇ × +∇ × + ∇ × = + AF A A A FF t n n tt t tn t n 2 1 nE E ˆ ×−= ( )0 2 1 ˆ ( ) S nH H J ×−= 2 1 nB B ˆ ⋅−= ( )0 2 1 ˆ ( ) S nD D ⋅−= ρ ( ) 2 1 S tS n n JJJ t ∂ρ ∇ ⋅ + − =− ∂ 1 1 ( ) S V 2 2 V E H dS B H D E dV J EdV t ∂ − × ⋅ = ⋅+ ⋅ + ⋅ ∂ ∫∫ ∫ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

第17讲时变电磁场(IV) 。正旋电磁场 ●正旋电磁场的复数表示 ·麦克斯韦方程组的复数形式 ·复介质参数 。复坡印亭矢量 。复坡印亭定理 ·时变电磁场的唯一性定理 ·波动方程 lexu@mail.xidian.edu.cn
第17讲 时变电磁场(Ⅳ) 正旋电磁场 正旋电磁场的复数表示 麦克斯韦方程组的复数形式 复介质参数 复坡印亭矢量 复坡印亭定理 时变电磁场的唯一性定理 波动方程 lexu@mail.xidian.edu.cn 3 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

正旋电磁场 ·时变电磁场,场量和场源既是时间的函数也是空间的函数 ·时变电磁场理论适用于任何时变场 ●】 正旋电磁场一时谐(time harmonic)电磁场 ●任意点的场矢量的每一坐标分量随时间以相同的频率作正旋 或余旋变化 在正旋稳态条件下,单频正旋场源在麦克斯韦方程组的约束 下激励的场强矢量各个坐标分量仍是同频的正旋时间函数 正旋电磁场的研究意义 。工程中激发电磁场的源多为正旋激励方式 通过傅里叶变换理论,任何时变电磁场都可以表示成为各个 单频正旋电磁磁场分量的叠加或积分 eu@maxidian.吧旋电磁场的研究是一切时变电磁场的基础
正旋电磁场 时变电磁场,场量和场源既是时间的函数也是空间的函数 时变电磁场理论适用于任何时变场 正旋电磁场——时谐(time harmonic)电磁场 任意点的场矢量的每一坐标分量随时间以相同的频率作正旋 或余旋变化 在正旋稳态条件下,单频正旋场源在麦克斯韦方程组的约束 下激励的场强矢量各个坐标分量仍是同频的正旋时间函数 正旋电磁场的研究意义 工程中激发电磁场的源多为正旋激励方式 通过傅里叶变换理论,任何时变电磁场都可以表示成为各个 单频正旋电磁磁场分量的叠加或积分 lexu@mail.xidian.edu.cn 正旋电磁场的研究是一切时变电磁场的基础 4 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
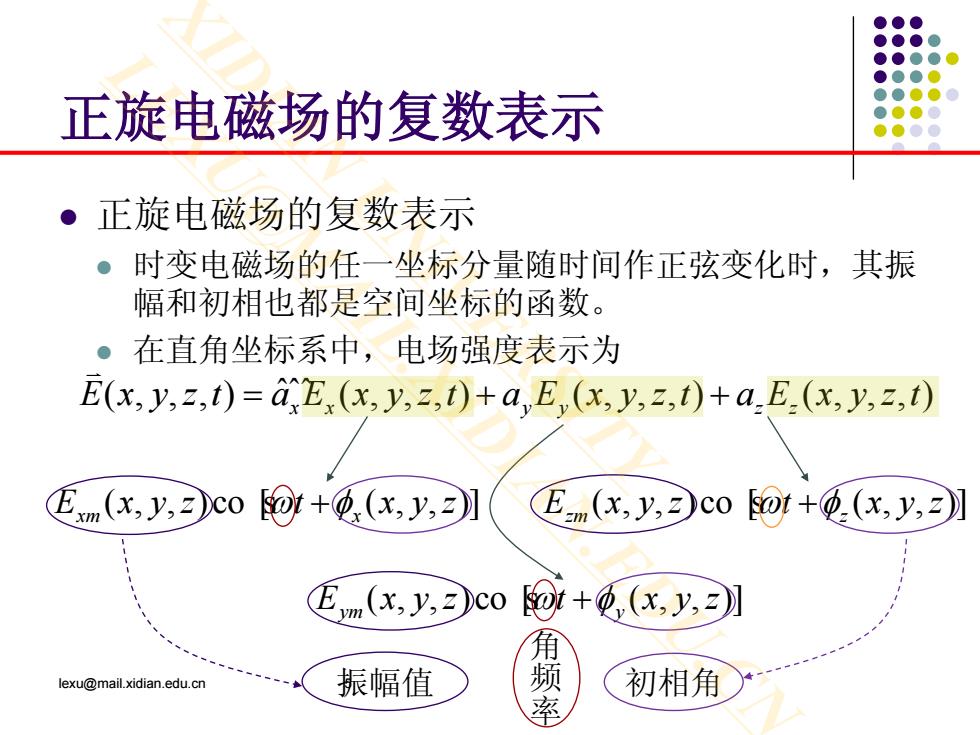
正旋电磁场的复数表示 。正旋电磁场的复数表示 。 时变电磁场的任一坐标分量随时间作正弦变化时,其振 幅和初相也都是空间坐标的函数。 ● 在直角坐标系中,电场强度表示为 E(x,y,z,t)=aE,(x,y,z,t)+a,Ey(x,y,z,t)+a.E_(x,y,z,t) Em(x,y,c0@t+项(x,y,】 Em(x,y,习Coot+(x,y,】 E(x.y.co @+更,(x,y,习〗 角 lexu@mail.xidian.edu.cn 振幅值 初相角
正旋电磁场的复数表示 正旋电磁场的复数表示 时变电磁场的任一坐标分量随时间作正弦变化时,其振 幅和初相也都是空间坐标的函数。 在直角坐标系中,电场强度表示为 lexu@mail.xidian.edu.cn 5 (, , ,) (, , ,) (, , ,) (, , ,) ˆˆˆ Exyzt aE xyzt aE xyzt aE xyzt =++ x x y y z z ( , , )co s[ ( , , )] E xyz t xyz ym ω φ+ y ( , , )co s[ ( , , )] E xyz t xyz xm ω φ+ x ( , , )co s[ ( , , )] E xyz t xyz zm ω φ+ z 振幅值 角频率 初相角 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
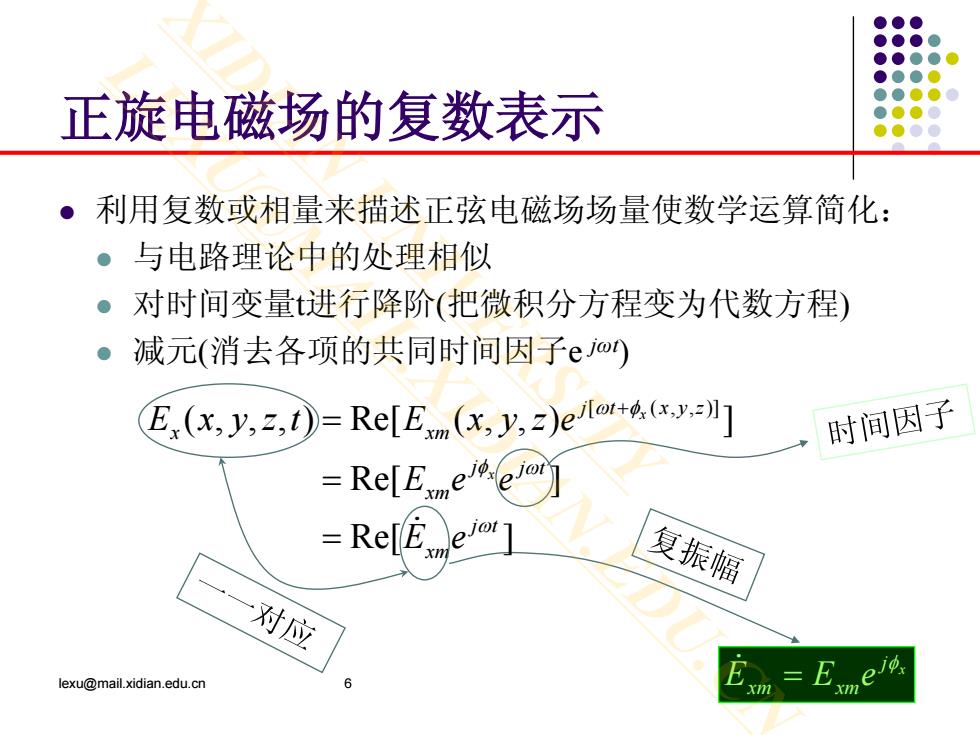
正旋电磁场的复数表示 ·利用复数或相量来描述正弦电磁场场量使数学运算简化: ●与电路理论中的处理相似 。对时间变量进行降阶(把微积分方程变为代数方程) ●减元(消去各项的共同时间因子ejw E(x,y,,1)=Re[E(x,y,)e/l] 时间因子 =RelE 复振幅 对应 lexu@mail.xidian.edu.cn E m
正旋电磁场的复数表示 利用复数或相量来描述正弦电磁场场量使数学运算简化: 与电路理论中的处理相似 对时间变量t进行降阶(把微积分方程变为代数方程) 减元(消去各项的共同时间因子e jωt) lexu@mail.xidian.edu.cn 6 x j xm xmeEE φ = [ ( , , )] ( , , , ) Re[ ( , , ) ] Re[ ] Re[ ] x x j t xyz x xm j j t xm j t xm E xyzt E xyze Ee e E e ω φ φ ω ω + = = = XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

正旋电磁场的复数表示 。复振幅仅是空间坐标的函数 复振幅包含场量的初相位,亦称相量(phasor) 。E,可以由复振幅与时间因子乘积的实部确定; 。 复振幅与E相互对应,也称为E的复数形式: E.(x,v,,t)Em(x,y,=)=E(x,y,)e) OE,(x,y,z,t) Ot =-E(x.y)on() Re[joEe] aE(x,y,2,2 lexu@mail.xidian.edu.cn 8t j@Ex(x,y
正旋电磁场的复数表示 复振幅仅是空间坐标的函数 复振幅包含场量的初相位,亦称相量(phasor) Ex可以由复振幅与时间因子乘积的实部确定; 复振幅与Ex相互对应,也称为Ex的复数形式; lexu@mail.xidian.edu.cn 7 (,,) (, , ,) (, , ) (, , ) x j xyz E xyzt E xyz E xyze x xm xm ↔ = φ ),,( ),,,( zyxEj t tzyxE xm x ↔ ω ∂ ∂ (, , ,) ( , , ) sin [ ( , , ) Re[ ] x xm x j t xm E xyzt E xyz t xyz t jEe ω ω ωφ ω ∂ =− ⋅ + ∂ = XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

正旋电磁场的复数表示 。电场强度矢量的复数表示 E(x,y.,t)=Rel(E+aa.E)e] =ReldEaEa.Eme] -RelEeto] 复(振幅)矢量 Ex,yz,)←Ex,ya=a它m+a,E,m+a.Em lexu@mail.xidi 西维函数←-三维函数
正旋电磁场的复数表示 电场强度矢量的复数表示 lexu@mail.xidian.edu.cn 8 ( , , , ) Re[( ˆˆˆ ) ] Re[ ˆˆˆ ) ] Re[ ] x y z j j j j t x xm y ym z zm j t x xm y ym z zm j t Exyzt aE e aE e aE e e aE aE aE e Ee φ φ φ ω ω ω = ++ = ++ = 复(振幅)矢量 (, , ,) (, , ) ˆˆˆ Exyzt Exyz aE aE aE ↔ =++ x xm y ym z zm 四维函数←→三维函数 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

正旋电磁场的复数表示 。例1将下列用复数形式表示的场矢量变换成瞬时值,或 作相反的变换 (1)E=aEo (2)E=djEoe (3)E=aE cos(ot-kz)+a,E sin(@t-kz) 。解] (1)E(x,y,z,t)=RelaEee]=a,E cos(ot+) (2)E(x.y.=.)-Reld.E.J-a.Eco(-k+) (3)E(x.y.=,1)=Reld.Ew-)-a Ee] lexu@mail.xidian.edu.cn E(x,员,z,t)=(a-aj)Ee]
正旋电磁场的复数表示 例1 将下列用复数形式表示的场矢量变换成瞬时值,或 作相反的变换 [解] lexu@mail.xidian.edu.cn 9 0 0 0 0 (1) ˆ (2) ˆ (3) cos( ) sin( ) ˆˆ x jkz x x y E aE E a jE e E a E t kz a E t kz ω ω − = = = −+ − 0 0 (1) ( , , , ) Re[ ] cos( ) ˆˆ x j j t E x y zt aEe e aE t x xx ϕ ω = = ω ϕ+ ( ) 2 0 0 (2) ( , , , ) Re[ ˆˆ ] cos( ) 2 j kz j t E x y z t a E e e a E t kz x x π ω π ω − = = −+ ( ) ( ) 2 0 0 (3) ( , , , ) Re[ ˆˆ ] j t kz j t kz E x y zt aEe aEe x y π ω ω − + − = − 0 (, , ,) ( ) ] ˆˆ jkz E x y zt a a j Ee x y − = − XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

正旋电磁场的复数表示 ·例2将下列场矢量的复数形式写为瞬时值形式 (1)E=a.Eo sin(kx)sin(ky)e (2)=dj2Esincos(k,cos0)ein ·解] (1)E=Re[Ee/]=a.Eo sin(k x)sin(kyy)cos(@t-k.2) (2)E=Re[Ee/W] =dRele2EsinOcos(k,Cos0)e =a,2E sinecos(k,cose)cos(ot-k.zsin+) lexu@mail.xidian.edu.cn =-a,2 sinecos(k,cose)sin(ot-k.zsine)
正旋电磁场的复数表示 例2 将下列场矢量的复数形式写为瞬时值形式 [解] lexu@mail.xidian.edu.cn 10 0 sin 0 (1) sin( )sin( ) ˆ (2) 2 sin cos( cos ) ˆ z z jk z z xy jk z x x E aE kx k ye E ajE k e θ θ θ − − = = 0 (1) Re[ ] sin( )sin( )cos( ) ˆ j t E Ee a E k x k y t k z z xy z ω = = ω − sin 2 0 0 0 (2) Re[ ] ˆ Re[ 2 sin cos( cos ) ] ˆ 2 sin cos( cos )cos( sin ) 2 ˆ 2 sin cos( cos )sin( sin ) z j t j jk z j t x x xx z xx z E Ee a eE k e e a E k t kz a E k t kz ω π θ ω θ θ π θ θω θ θ θω θ − = = = − + = − − XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

麦克斯韦方程组的复数形式 复数运算中,复数的微分运算以及积分运算可以对实部虚 部分别进行运算 LZ]=LIx]+iLly] 。其中L为实线性算子 。对于复数表示的电磁场场量的相应运算亦可利用该性质: V×i(r,t)=j(r,t)+ aD(r,t) Ot VxReli(]-Rel(+RelD()e] RexRel(R(e
麦克斯韦方程组的复数形式 复数运算中,复数的微分运算以及积分运算可以对实部虚 部分别进行运算 其中L为实线性算子 对于复数表示的电磁场场量的相应运算亦可利用该性质: lexu@mail.xidian.edu.cn 11 L Z L x iL y [ ] [] [] = + , ,, dt t ∂ ∇ ∂ ∫ (,) (,) (,) Drt Hrt Jrt t ∂ ∇× = + ∂ Re[ ( ) ] Re[ ( ) ] Re[ ( ) ] j t j t j t Hre Jre Dre t ωω ω ∂ ∇ × = + ∂ Re[ ( ) ] Re[ ( ) ] Re{ [ ( ) ]} j t j t j t Hre Jre Dre t ωω ω ∂ ∇× = + ∂ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN