
u 第24讲电磁波的辐射(〉 电磁波的辐射 滞后位 ■电基本振子的电磁场计算 ■电基本振子的电磁场分析 ·磁基本振子的辐射场 DFAN.EDU.CN lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 2 第24讲 电磁波的辐射(I) 电磁波的辐射 滞后位 电基本振子的电磁场计算 电基本振子的电磁场分析 磁基本振子的辐射场 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

电磁波的辐射 ■ 电磁波的传播 ·电磁波在无界空间的传播 ·电磁波在不同介质分界面上的反、透射问题 ■电磁波的辐射和接收 ·电磁波的辐射:时变电磁场能量可以脱离场源以电磁 波的形式在空间向远处传播而不再返回场源: ·电子系统中辐射或接收电磁波的装置称为天线 ■ 电磁波的场源 ·天线上的时变电流或电荷 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 3 电磁波的辐射 电磁波的传播 • 电磁波在无界空间的传播 • 电磁波在不同介质分界面上的反、透射问题 电磁波的辐射和接收 • 电磁波的辐射:时变电磁场能量可以脱离场源以电磁 波的形式在空间向远处传播而不再返回场源; • 电子系统中辐射或接收电磁波的装置称为天线 电磁波的场源 • 天线上的时变电流或电荷 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

电磁波的辐射 ■天线激发的电磁场 ·天线上的电流与它激发的电磁场相互作用 ·天线的电流激发空间磁场→空间电磁场影响天线的 电流分布 ·天线辐射问题本质上是一个边值问题,根据天线满足 的边界条件求解麦克斯韦方程组 ● 实际上这样的边值问题很难求解,更常用的方式是采 用近似解法把它处理成为一个分布型问题: ·首先求解天线上的场源分布 ◆ 根据场源分布求解外场 ■天线的型式:线天线和面天线 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 4 电磁波的辐射 天线激发的电磁场 • 天线上的电流与它激发的电磁场相互作用 • 天线的电流激发空间磁场←→空间电磁场影响天线的 电流分布 • 天线辐射问题本质上是一个边值问题,根据天线满足 的边界条件求解麦克斯韦方程组 • 实际上这样的边值问题很难求解,更常用的方式是采 用近似解法把它处理成为一个分布型问题: 首先求解天线上的场源分布 根据场源分布求解外场 天线的型式:线天线和面天线 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

滞后位 时谐电磁场的位方程: V2A+k2A=-uJ =0u8 V20+k20月 。称为非齐次亥姆赫兹方程 ·时谐场中的电流连续性方程: 又.j=-j0p ·洛仑兹条件: V.A=-j0480 电磁场与位函数 E=-j0 VV·A) B=VxA lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 5 滞后位 时谐电磁场的位方程: • 称为非齐次亥姆赫兹方程 • 时谐场中的电流连续性方程: • 洛仑兹条件: • 电磁场与位函数 2 2 ∇ + =− A kA J µ 2 2 k ρ ϕ ϕ ε ∇ + =− ∇⋅ =− J jωρ ∇⋅ =− A jωµεϕ B A =∇× 2 ( ) A Ej A k ω ∇ ∇⋅ = − + 2 k =ωµε XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

滞后位 ■亥姆霍兹积分及辐射条件 ·格林定理 [(uVw-wVu)d E(uVw-wVu).dS u和w是任意标量函数, ■和w以及它们的一阶和二阶导数在V内连续。 ● 验证标量函数ψ是齐次亥姆赫兹方程的一个解 R ⊙ V20+k2w=0 R lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 6 滞后位 亥姆霍兹积分及辐射条件 • 格林定理 u和w是任意标量函数, u和w以及它们的一阶和二阶导数在V内连续。 • 验证标量函数ψ是齐次亥姆赫兹方程的一个解 2 2 ( )( ) V S u w w u d V u w w u dS ∇ −∇ = ∇−∇ ⋅ ∫ ∫ R e− jkR ψ = 0 22 k ψψ =+∇ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
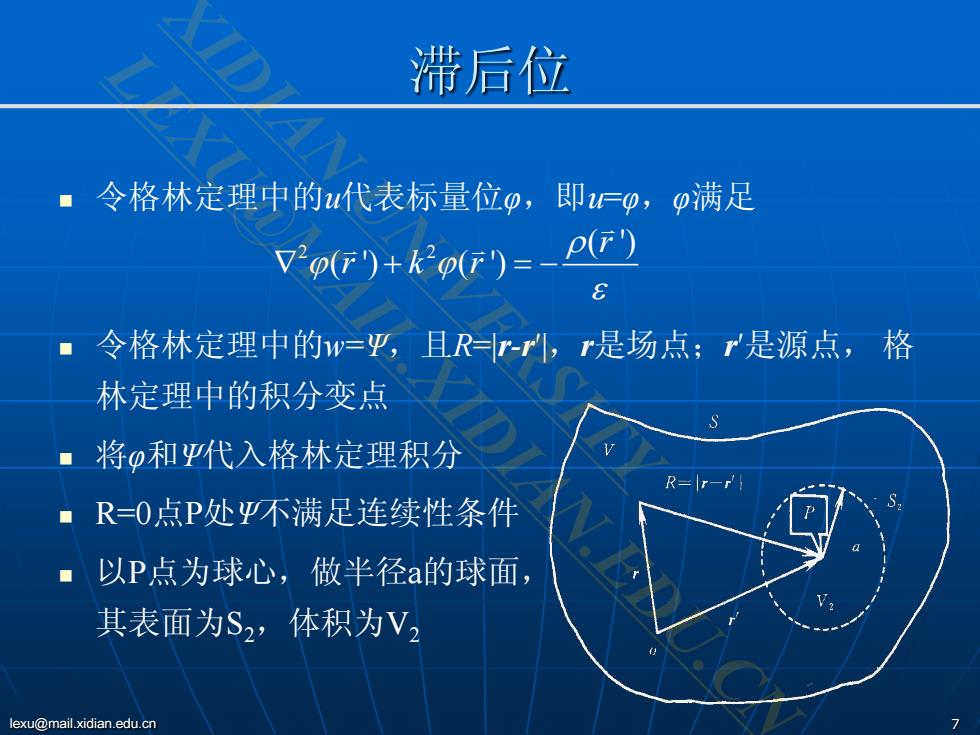
滞后位 ■令格林定理中的u代表标量位p,即厂p,p满足 o)+CF)=-pF】 ■令格林定理中的w=平,且Rr-,r是场点;r是源点,格 林定理中的积分变点 ■将φ和平代入格林定理积分 R=r-r ·R=O点P处平不满足连续性条件 以P点为球心,做半径a的球面, 其表面为S2,体积为V2 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 7 滞后位 令格林定理中的u代表标量位φ,即u=φ,φ满足 令格林定理中的w=Ψ,且R=|r-r′|,r是场点;r′是源点, 格 林定理中的积分变点 将φ和Ψ代入格林定理积分 R=0点P处Ψ不满足连续性条件 以P点为球心,做半径a的球面, 其表面为S2,体积为V2 2 2 ( ') ( ') ( ') r r kr ρ ϕ ϕ ε ∇ + =− XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

滞后位 格林积分在体积V=VV,及表面S,=S+S,上进行 J【oF)y-Wp()' or) ap(') - ds+ oo(r ds"' On S,上面积分,外法线方向指向小球球心P点 0/0n=-0/0R 面元dS'=a2dQ',d2'是dS对P点所张立体角元。 p(F) ads' aR R R aR e(r) Rap(T ads R aR R≥a lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 8 滞后位 格林积分在体积V1 =V-V2及表面S1 =S+S2上进行 • S2上面积分,外法线方向指向小球球心P点 • 面元dS’=a2dΩ’ ,dΩ’是dS’对P点所张立体角元。 1 2 2 2 [ ( ') ( ')] ' ( ') ( ') ( ') ' ( ') ' V S S r r dV r r r dS r dS n n n n ϕ ψψ ϕ ψ ϕ ψ ϕ ϕψ ϕψ ∇ −∇ = ∂ ∂ ∂ ∂ −+− ∂ ∂ ∂ ∂ ∫ ∫ ∫ =∂∂ −∂ // ∂Rn 2 2 2 2 2 ( ') ( ') ' 1 ( ') ( ') ' jkR jkR S R a jkR jkR S R a ee r r a d RR R R jk e r r e a d RR R R ϕ ϕ ϕ ϕ − − = − − = ∂ ∂ −+ Ω ∂ ∂ ∂ = ++ Ω ∂ ∫ ∫ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

滞后位 eag】 adg 令a→0,小球面S,收缩成点P aR ■ Op/OR有限,积分只剩下被积函数是or)ejkR/R2的一项 不等于零 小球面S2上的pr)可以用小球球心处的(r)代替 a'd"=or),dQ'=4ro(r) 考虑到y及0满足的方程,体积V,和面积S,上的格林定 理积分可写成 2。d+ aoF))e题 8e-ikR ds R 4π On R On R lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 9 滞后位 令a→0,小球面S2收缩成点P 有限,积分只剩下被积函数是φ(r’) e-jkR/R2的一项 不等于零 小球面S2上的φ(r’)可以用小球球心处的φ(r)代替 • 考虑到ψ及φ满足的方程,体积V1和面积S1上的格林定 理积分可写成 ϕ / ∂∂ R 2 2 2 2 0 lim ( ') ' () ' 4 () jkR a S S R a e r ad r d r R ϕ ϕ πϕ − → = Ω= Ω= ∫ ∫ 1 ( ') 1 ( ') ( ) ' ( ') ' 4 4 jkR jkR jkR V S r re e r e dV r dS R n R nR ρ ϕ ϕ ϕ πε π − − − ∂ ∂ = +− ∂ ∂ ∫ ∫ 2 2 2 1 ( ') ( ') ' jkR jkR S R a jk e r r e a d RR R R ϕ ϕ − − = ∂ ++ Ω ∂ ∫ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

滞后位 由标量位函数的解可知矢量位函数的解为 4π o e-jkR 4π5 On On R 。已知场源分布即可求得位函数 ●体积分是V中场源的贡献 ·面积分是V外场源的贡献 称为亥姆霍兹积分 N.EDU.CN lexu@mail.xidian.edu.cn 10
lexu@mail.xidian.edu.cn 10 滞后位 由标量位函数的解可知矢量位函数的解为 • 已知场源分布即可求得位函数 • 体积分是V中场源的贡献 • 面积分是V外场源的贡献 • 称为亥姆霍兹积分 ( ') ( ) ' 4 1 ( ') ( ') ' 4 jkR V jkR jkR S J r A r e dV R Ar e e A r dS n R nR µ π π − − − = ∂ ∂ + − ∂ ∂ ∫ ∫ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

滞后位 ■对于无限空间的电磁问题,取以R为半径的球面作 为S,dS'=R2Q',亥姆霍兹积分中的面积分为 要排除在无限远处的场源(设无限远处的场源为零),就 必须使上式为零。为此,要求R→c时 mRp三有限值 此时第二项积分等于零,即要求在远离场源处标量位④ 至少按R1减少; 第一项积分在满足辐射条件时也为零 lim R +k0 =0 R→0 lexu@mail.xidian.edu.cn aR
lexu@mail.xidian.edu.cn 11 滞后位 对于无限空间的电磁问题,取以R为半径的球面作 为S,dS’=R2dΩ’,亥姆霍兹积分中的面积分为 • 要排除在无限远处的场源(设无限远处的场源为零), 就 必须使上式为零。为此,要求R→∝时 • 此时第二项积分等于零, 即要求在远离场源处标量位φ 至少按R-1减少; • 第一项积分在满足辐射条件时也为零 '+Ω Ω' + ∂ ∂ − − ∫ ∫ jk dede R R jkR S jkR S ϕ ϕ ϕ = 有限值 ∞→ Rϕ R lim lim = 0 + ∂ ∂ ∞→ ϕ ϕ jk R R R XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN