
习题课
习题课

1、质量为0.10kg的物体,以振幅1.0×10-2m 作简谐运动,其最大加速度为4.0ms2,求: (1)振动的周期; (2)通过平衡位置的动能; (3)总能量; (4)物体在何处其动能和势能相等? 解(1)aax=A01 =20s A 2元=0.314s 011:.1
1、 质量为 的物体,以振幅 作简谐运动,其最大加速度为 ,求: 0.10kg 1.0 10 m −2 2 4.0m s − (1)振动的周期; (2)通过平衡位置的动能; (3)总能量; (4)物体在何处其动能和势能相等? 解 (1) 2 amax = A A amax = 1 20s − = 0.314s 2π = = T

1 1 (2) Ems=2m加=2mw2N=2.0x105J 2 (3)E=Ekmx=2.0×103J (4)Ek=E,时,E。=1.0×103J 2E=0.5×10'm2 mo x=±0.707cm
( 2 ) 2 . 0 10 J − 3 = 2 2 2 k,max max 21 21 E = m v = m A ( 3 ) E = E k ,max 2 . 0 10 J − 3 = ( 4 ) E k = E p 时, 1 . 0 10 J 3 p − E = 由 2 2 2 p 21 21 E = k x = m x 2 2 2 p m E x = 4 2 0 . 5 10 m − = x = 0 .707cm

2、给出下列波函数所表示的波的传播方向 和x=0点的初相位. y=-1cos2x(号克→y=4eo2m7克+别 (向X轴正向传播p=兀) 少=4cosa(-i-》→y=co(+说+l (向x轴负向传播( =元) 011:.1 10+7:后5
2、给出下列波函数所表示的波的传播方向 和 x = 0 点的初相位. cos 2π ( ) x T t y = −A − cos ( ) u x y = −A −t − ( 向x 轴正向传播 , =π ) ( 向x 轴负向传播 , =π ) cos[2π( ) ] t x y A T = − + cos[ ( ) ] x y A t u = + +

3、平面简谐波的波函数为 y=Acos(Bt-Cx) 式中A,B,C为正常数,求波长、波速。 y=Acos(Bt-Cx) y=4c0s2x(分2》 2π T= 2π B u B T
3、平面简谐波的波函数为 式中 为正常数,求波长、波速。 y = Acos(Bt −Cx) A,B,C y = Acos(Bt −Cx) cos 2 π ( ) x T t y = A − C 2π = B T 2π = C B T u = =

第五节 简谐波 习题5-8试利用能流密度的 概念求球面波的表达式。 解介质无吸收,单位时间 通过两个球面的能流相等: IS =12S2 即 ptou-2p5ou月 1 2 A1=乃 y=4 cosou-) A 中Y为离开波源的距离,A,为r=1处的振幅
习题5-8 试利用能流密度的 概念求球面波的表达式。 解 介质无吸收,单位时间 通过两个球面的能流相等: 1 s 2 s 1 r 2 r 1 2 2 1 r r A A = 0 cos ( ) A r y t r u = − 1 1 2 S2 I S = I 2 2 2 2 2 2 1 2 2 1 4π 2 1 4π 2 1 即 A u r = A u r 第五节 简谐波 式中 r 为离开波源的距离, 为 r =1 处的振幅. A0
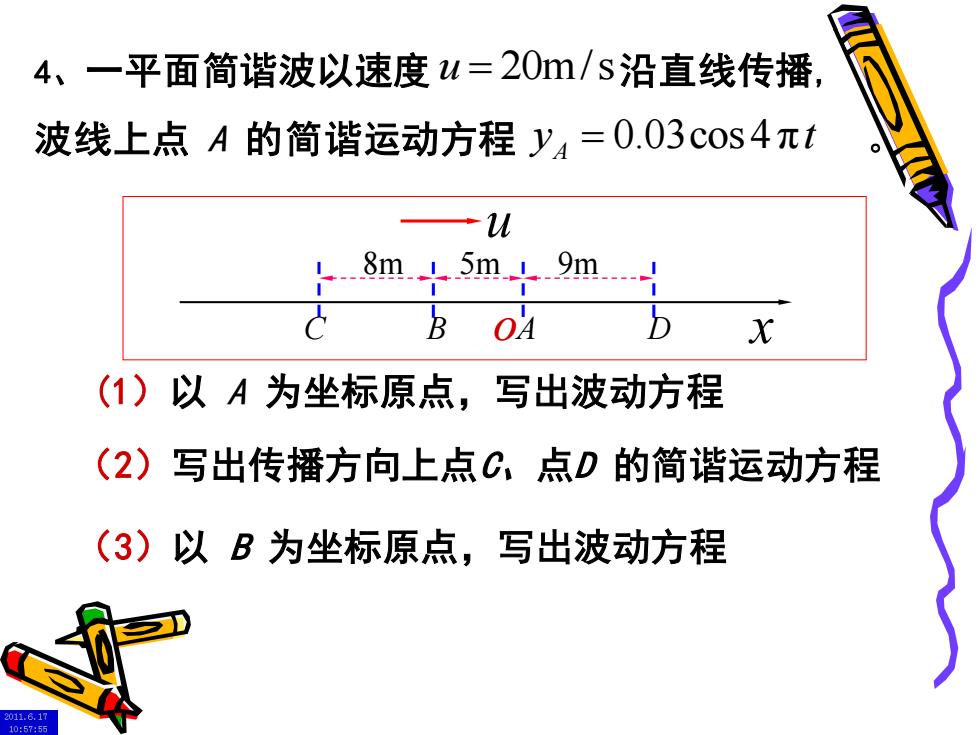
4、一平面简谐波以速度u=20m/s沿直线传播, 波线上点A的简谐运动方程y4=0.03c0s4πt ↓8m.↓5m.4.9m X (1)以A为坐标原点,写出波动方程 (2)写出传播方向上点C,点D的简谐运动方程 (3)以B为坐标原点,写出波动方程
4、一平面简谐波以速度 沿直线传播, 波线上点 A 的简谐运动方程 。 u = 20m/s 0.03cos 4π A y t = (1)以 A 为坐标原点,写出波动方程 u C B A D 5m 9m o x 8m (3)以 B 为坐标原点,写出波动方程 (2)写出传播方向上点C、点D 的简谐运动方程

4、一平面简谐波以速度u=20m/s沿直线传播, 波线上点A的简谐运动方程y4=0.03c0s4πt 卜8m.十5mh9m寸 B OA (1)以A为坐标原点,写出波动方程 A=0.03mT=0.5sp=02=T=10m y=4cos[2x(72+例 y=0.03cos2π0.5 10
4、一平面简谐波以速度 沿直线传播, 波线上点 A 的简谐运动方程 。 u = 20m/s 0.03cos 4π A y t = (1)以 A 为坐标原点,写出波动方程 u C B A D 5m 9m o x 8m A= 0.03m T = 0.5s = 0 = uT =10m 0.03cos 2π( ) 0.5 10 t x y = − cos[2π ( ) ] = − + x T t y A

(2)写出传播方向上点C,点D的简谐运动方程 8m↓5m9m B OA 比 y=003eos2x05& k=0.03c0s2π(片-3)=0.03c0s4t+ 13 0.5 10 5 %=0.03cos2m0510=0.03cos(4t- 9
u C B A D 5m 9m o x 8m 0.03cos 2π( ) 0.5 10 t x y = − (2)写出传播方向上点C、点D 的简谐运动方程 13 13 0.03cos 2π( ) 0.03cos(4π ) 0.5 10 5 C t y t − = − = + 9 9 0.03cos 2π( ) 0.03cos(4π ) 0.5 10 5 D t y t = − = −

(3)以B为坐标原点,写出波动方程 y4=0.03cos4πt → 1.8m.+5m+.9m.d C OB A D 26 △0=pg-04= 三元 PB=元 yB=0.03cos(4πt+π) y=003s25+
=π B =π 0.03cos(4π π) B y t = + 0.03cos[2π( ) π] 0.5 10 t x y = − + u C B A D 5m 9m o x 8m y t A = 0.03cos 4π (3)以 B 为坐标原点,写出波动方程 2 B A = − =