
稳恒磁场习题课 4>>g
稳恒磁场习题课

一本章主要内容回顾 1.磁场的来源 2.表述磁场的方法 3.磁通量 B.dS
一 .本章主要内容回顾 1.磁场的来源 2.表述磁场的方法 3.磁通量 = s m B dS

4.磁场的计算 1)毕奥-萨伐尔定理 dB to Idl x元 4π 电流产生磁场 微观叠加 B- Idl×F B=「dB 4 B=∑B, 场叠加 2)安培环路定理 f,BdI=4o∑I 3)运动电荷产生的磁场 = L0δ×F 4元 3
4.磁场的计算 1)毕奥-萨伐尔定理 3 0 4 r Idl r dB = 电流产生磁场 = 3 0 4 r Idl r B B = dB B = Bi 微观叠加 场叠加 2)安培环路定理 = i l B dl I 0 3)运动电荷产生的磁场 3 0 4 r q r B =

5.磁场方程 1)磁场高斯定理 、B:d5 =0 (稳恒磁场无源) 2)安培环路定理 f,BdI=4∑I (稳恒磁场有旋) 6.载流线圈的磁矩 NISn 7.电磁相互作用 1)安培定律 f ldl x B 2)磁场对载流导线的安培力 =∫dI×B 3)磁场对载流线圈的作用力矩 M=P,×B
5.磁场方程 1)磁场高斯定理 = S B dS 0 (稳恒磁场无源) 2)安培环路定理 l = i B dl I 0 (稳恒磁场有旋) 6.载流线圈的磁矩 Pm NISn = 7.电磁相互作用 1)安培定律 df Idl B = 2)磁场对载流导线的安培力 = l f Idl B 3)磁场对载流线圈的作用力矩 M Pm B = I S n

4)磁场对运动电荷的洛仑兹力 F=gU×B 8.霍耳电压 RH IB (RH D
4)磁场对运动电荷的洛仑兹力 F q B = 8.霍耳电压 b IB UH = RH ) 1 ( nq RH =
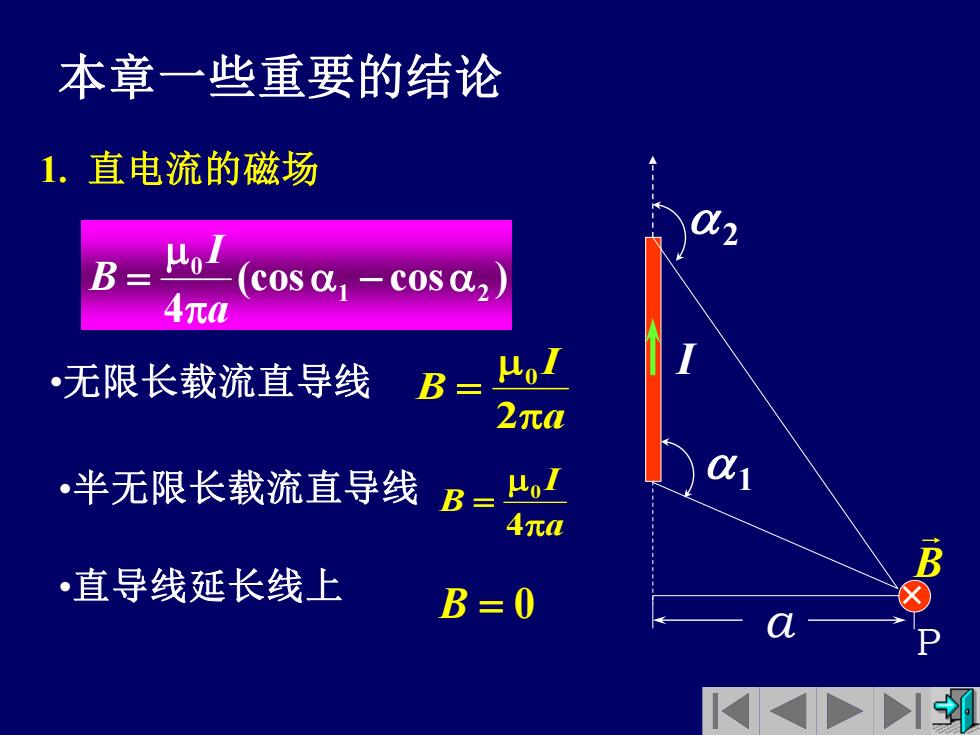
本章一些重要的结论 1.直电流的磁场 o (c0s01-C0S02) 4元 无限长载流直导线B= 2元0 •半无限长载流直导线 B- 4元a •直导线延长线上 B=0
1. 直电流的磁场 a P 1 2 I B (cos cos ) 4 1 2 0 − = a I B •无限长载流直导线 a I B = 2 0 •半无限长载流直导线 a I B = 4 0 •直导线延长线上 B = 0 本章一些重要的结论


2.圆电流轴线上某点的磁场 HoIR2 R 大小: B 2(R2+x2)32 方向: 右手螺旋法则 (1)载流圆环圆心处的B圆心角0=2元 B 2R (2)载流圆弧圆心角0 B Lo! -=4I8 2R2元 4元R
2. 圆电流轴线上某点的磁场 2 2 3 2 2 0 2( R x ) IR B + = 方向: 右手螺旋法则 大小: (1) 载流圆环圆心处的 B 圆心角 = 2 R I B 2 0 = (2) 载流圆弧 圆心角 R I R I B 2 2 4 0 0 = • = R x I P x

静电场 比较 磁场 ∮E.dl=0 5B.dl=o∑I; 电场有保守性,它是 磁场没有保守性,它是 保守场,或有势场 非保守场,或无势场 E=9 JB●5=0 80 电力线起于正电荷、 磁力线闭合、 止于负电荷。 无自由磁荷 静电场是有源场 磁场是无源场
E dl = 0 静电场 磁 场 = i i B dl I 0 B • ds = 0 • = i s E ds q 0 1 比较 ? 磁场没有保守性,它是 非保守场,或无势场 电场有保守性,它是 保守场,或有势场 电力线起于正电荷、 止于负电荷。 静电场是有源场 磁力线闭合、 无自由磁荷 磁场是无源场

电偶极子 类比 磁偶极子 2a i S P=ql 在轴延长线上某点 B o Pm 2元E0 3 2元 3
电偶极子 磁偶极子 n I S 3 0 2 r p B m = p m ISn = 3 2 0 1 r p E e = P ql = 类 比 在轴延长线上某点 • • − q q l